一本通-数据排序

1.选择排序

	for(int i = 1; i <= n-1; i++){
		int t = i;
		for(int j = i+1; j <= n; j++){
			if(a[j] < a[t])	t = j;
		}
		swap(a[t],a[i]);
	}

---

 

2.冒泡排序

	for(int i = 1; i <= n-1; i++){
		for(int j = 1; j <= n-1; j++){
			if(a[j] > a[j+1]) swap(a[j],a[j+1]);
		}
	}

 改进的冒泡排序

	for(int i = 1; i <= n-1; i++){
		bool ok = true;
		for(int j = 1; j <= n-1; j++){
			if(a[j] > a[j+1]){
				swap(a[j],a[j+1]);
				ok = false;
			}
		}
		if(ok) break;
	}

---

 

3. 插入排序

	for(int i = 2; i <= n; i++){
		int t = a[i];
		int j;
		//从i的前一位开始扫描
		for(j = i-1; j >= 1; j--){
			if(a[i] > a[j]) break;
		}
		//a[j+1]~a[i-1] 后移一位
		for(int k = i-1; k >= j+1; k--) a[k+1] = a[k];
		a[j+1] = t;
	}

---

 

4.桶排序

	for(int i = 1; i <= n; i++){
		b[a[i]]++;
	}
	for(int i = 1; i <= n; i++){
		while(b[i] > 0){
			cout << i << " ";
			b[i]--;	
		}
	}	

---

---

 

 5.快速排序

方案一：pivot为第一个数，使用轮换方法

void quickSort(int a[],int l,int r){
	if(l >= r) return;
	int i = l,j = r;
	int pivot = a[i];
	//两指针相遇，即可退出赋值
	while(i < j){
		//i < j是因为相遇时，保持相遇状态，i,j指针不动，等待赋值结束。
		// >=pivot 等号都可以去掉，如果去掉，交换的次数多一点点。 
		while(a[j] >= pivot && i < j) j--;
		a[i] = a[j];
		while(a[i] <= pivot && i < j) i++;
		a[j] = a[i];
	}
	a[i] = pivot; //期望位置，ij指针相同的位置
	quickSort(a,l,i-1);
	quickSort(a,i+1,r);
}

首先解释一下算法的大致思路，pivot = a[l], 备份第一个元素，此时a[l]空闲，a[l] 盛放从右边开始查找的比pivot小的元素a[j]，

置换过后，此时a[j]空闲，a[j]盛放从左边开始查找的比pivot大的元素，

以此循环 ，达到交换的目的，直到i,j 指针重合，当i，j指针重合后，内外层循环结束，a[i] = a[j] 是空闲的区域，将pivot拷贝至此，pivot的位置就是最终位置。

下面来解释外层循环while为什么要 i < j 而不是 i<=j:

什么时候会造成 i== j？ 内层的两个while循环均可造成 i== j 。

比如，左边a[j] 空闲，现在执行第一个while循环，指针j从右边开始找，j --, 此时 i== j , 执行a[i] = a[j] (无效拷贝)，第二个循环就不满足了(因为 i < j 不成立),  a[i] == a[j] 是空闲的，到这里就执行结束了，外层循环就不需要执行了，所以外层循环是 i < j

另外一种情况是，执行第一个while循环，j--,找到一个元素a[j] < pivot,  拷贝到左边的空闲元素a[i] 之后，此时a[j]空闲，现在执行第二个循环，从左边执行i++寻找a[i] > pivot拷贝到右边。 i++一直执行都未找到, 此时 i == j, a[i] = a[j] (无效拷贝), 执行到这里，交换就可以结束了，所以外层循环是 i < j。

当然外层循环写成while(i <= j）执行结果也没有影响，内层两个while循环也不会执行，a[i] = a[j] , a[j] = a[i] ，属于无效拷贝。

外层while i < j 写不写等于号要思考清楚啊--!

下面来解释递归前为什么要写if判断条件：

当递归过程中只有一个元素，i、j重合后， l == i == j , i-1 < l , 递归时就要判断条件    if(l < i-1) ,

这只是一个特殊情况，下面看所有的情况

1.当数组第一个元素最小（也是支点），l == i == j == 第一个下标， 也要判断条件if(l < i-1) 

2. 当数组第一个元素最大, 循环一次后，i == j == r == 最后一个元素的下标，这时就要判断条件 if(i+1 < r), 否则就要越界

下面来解释内存循环为什么是 a[j] >= pivot 而不是 a[j] > pivot ?

其实，去掉等于号，也不影响算法的执行结果。

当写pivot时，扫描到a[j] == pivot 时 忽略到 此 a[j] 寻找比 pivot 小的元素，因为此时数组有至少两个pivot值相同的元素了，pivot可以不处理。

只要最终pivot左边的元素小于等于pivot，右边的元素大于等于pivot就行了，pivot的位置也是该值得最终位置。

去掉等号，与pivot相等的值也参与交换过程，多了几次交换而已，只要保证一开始的支点元素到最终位置就行，和支点相同的元素到哪边都行，不考虑最方便

内层第二个while循环的  i < j 是为了控制，当第一个while循环到达了i== j，就可以退出循环了。

那么第一个while循环的 i < j 是为了啥呢。

是因为：如果第一元素最小，此时 j -- ,一直找不到比pivot小的元素，防止 j 下标 越界。

那么，第二个while 循环的 i  < j 有没有防止越界的功能呢？

如果第一个元素最大，执行第一个while循环后，a[r] 空闲，然后执行第二个while循环 i++, 一直找，直到 i == j  == r 不满足a[i] <= pivot 了， 他会自己停下来，所以没有防止越界的功能。

如果pivot选择最后一个元素，就有了防止越界的功能。

方案二：pivot为第一个数，使用交换方法

i，j 指针最后重叠后，什么时候与a[l] 交换，交换的正确性是要讨论的，其他的方面临界条件与方案一相似

i，j指针重叠后为什么是a[l]的最终位置？

好像和第一个内层while循环有关， 每一个外层循环，就找到一对进行交换。

如果，a[l] 元素最小，j -- , j-- ..... 知道 i == j = a[l] ， 所有的循环就终止了，swap(a[l],a[i]) 属于无效交换。

如果，a[l] 元素最大，a[j] = a[r-1] ,  i++ , i++........直到 i == j == a[r-1] , swap(a[i],a[j]) 属于无效交换。

void quickSort(int a[],int l ,int r){
	if(l >= r) return;
	int i = l,j = r;
	int pivot = a[l];
	while(i < j){
		while(a[j] >= pivot && i < j) j--;
		while(a[i] <= pivot && i < j) i++;
		if(i < j) swap(a[i],a[j]);
	}
	swap(a[i],a[l]);
	quickSort(a,l,i-1);
	quickSort(a,i+1,r);
}

有四种情况，第一种情况，第一个while循环找到比支点小的数，第二个while循环找到比支点大的数，进行交换，这样子没问题。

第二种情况，第一个while循环找到比支点小的数，第二个while循环找不到，i，j指针就重合了，不交换，i下标是不是支点a[l]的最终位置呢？第三种情况第一个while循环找不到比支点小的数，i，j就重合了，这种情况属于支点是最小的数。第四种情况是第一个while循环和第二个while循环都找不到，这种情况也属于第一个while循环找不到的情况

第三种情况属于支点是最大的情况，首先执行j--,右边第一个数就是比支点小的数。然后i++，i++......直到i＝＝j，执行i++的过程中，略过的数据都是比支点小的数，支点与最后一个数交换就是最终位置。其他的数都是比支点小啊。

考虑最终位置，就要考虑i，j相等的触发情况。

第一个while循环触发是因为，当前查找区间内所有的数都比支点大，找不到比支点小的数，j--，j--直到 i==j，结束所有循环，此时区间最左边的位置就是pivot的最终位置，因为他右边的值都比支点大。第二个while循环触发结束循环，是因为当前查找区间的所有值都比支点小，i++找不到比支点大的值，所以此时查找区间的最右边的位置就是支点的最终位置，因为其他位置都比支点小。

方案一无论哪个内层while循环触发，i==j，都是空闲位置，都是支点的最终位置

方案三：pivot为中间的值，使用交换方法

void quickSort(int a[],int l, int r){
	if(l >= r) return;
	int i = l,j = r;
	int pivot = a[(l+r)/2];
	while(i <= j){
		while(a[j] > pivot) j--;
		while(a[i] < pivot) i++;
		if(i <= j){
			swap(a[i],a[j]);
			i++;
			j--;
		}
	}
	quickSort(a,l,j);
	quickSort(a,i,r);
}

为什么内层循环是a[j] > pivot 而不是  a[j] >= pivot ?  

是因为pivot是在中间，如果是 >= , 则会一直 j-- , j -- ......会造成越界。

为什么外层循环是 i < j , 而不是  i <= j ? 

因为递归条件是 , [l , r] , [i, r] ， i和j 必须见面后，背靠背走一步。当 i== j 时，再执行一次循环。此时 a[i] == a[j] == pivot, 内层的两个while循环不执行，swap(a[i],a[j])属于无效交换。 i++，j-- 分离一步即可。

执行结束后，pivot 左边的一定比pivot小吗，右边的一定比pivot大吗？ 执行的结果正确吗？

因为是 a[j] > pivot ， 如果有和pivot值相同的元素则不考虑。

有两种情况使i== j ，使条件终止，第一种情况是，第一个while循环，从右边开始找，此时的pivot在最左边， j--, j--......一直找不到比pivot小的元素。直到 i == j ，此时a[i] == a[j] == pivot, 第二个while循环不执行，swap无效交换后， i++,j-- 背靠背走一步相离开

方案三的另外一种写法

void quickSort(int a[],int l, int r){
	if(l >= r) return;
	int i = l-1,j = r+1;
	int pivot = a[(l+r)>>1];
	while(i < j){
		do i++;while(a[i] < pivot);
		do j--;while(a[j] > pivot);
		if(i < j) swap(a[i],a[j]);
	}
	quickSort(a,l,j);
	quickSort(a,j+1,r);
}

我们来讨论边界问题的正确性。使外层循环的终止条件不是 i == j。造成这种情况有两种原因，第一个while循环，或者是第二个while 循环。

此算法不能保证在 i == j 时停下来。且支点不在最终位置。

递归区间是什么？

每次执行内层的while循环，都是在上次执行的结果上，走一步。

第一个while循环停止的时候是, 找到a[i] >= pivot,  一定会找到。

第二个while循环停止的时候是，找到一个a[j] <= pivot, 一定会找到。

什么时候会停止呢？

当支点最小，且执行第一个while循环后, a[i] == pivot, 然后执行第二个while循环，j -- , j-- ......找不到比 pivot小的数，直到 a[i] == a[j] == pivot。这个时候  i == j

当支点被交换过后，此时的查找区间内的所有数都比pivot大，执行一个while循环 a[i] > pivot, i 指针会停在当前查找区间第一个数，然后执行第二个while循环，j--, j-- ....会比i小 ， j == i-1, j指针指向的位置就是刚才未交换前支点的最终位置。j 就是分界点。

这也是递归区间 “不分叉” 的原因，支点不在最终的位置，不能用此方法求第k大值。

 

---

---

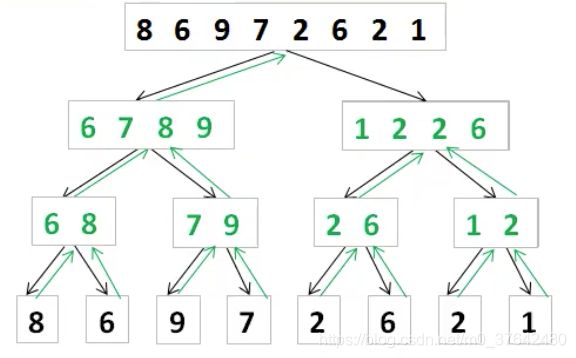
6. 归并排序 

归并排序主要分为两大步 , 归并，排序。

void msort(int a[],int l,int r){
	if(l == r) return;
	//划分
	int mid = (l+r)/2;
	msort(a,l,mid);
	msort(a,mid+1,r);
	//归并
	int i = l,j = mid+1,k = l;
	while(i <= mid && j <= r){
		if(a[i] > a[j]) b[k++] = a[j++];
		else b[k++] = a[i++];
	}
	//处理没有完全归并的一半
	while(i <= mid) b[k++] = a[i++];
	while(j <= r) b[k++] = a[j++];
	//b数组拷贝至原数组a
	for(int i = l; i <= r; i++) a[i] = b[i];
}

归并的过程为什么可以计算逆序对数呢？

每个数字递归到最后一层后，每个数字向树的最顶端返回时，从最少的数进行比对逆序数。

从单个数字来看，在返回的过程中，该数字对比的数字越来越多。