常见的几种排序方法_计数排序,基数排序,桶排序,选择排序,冒泡排序,插入排序,希尔排序,归并排序,快速排序_1
文章目录
-
- 算法的优劣
- 计数排序
- 基数排序
- 桶排序
- 选择排序
- 冒泡算法
- 插入排序
- 希尔排序
- 归并排序
- 快速排序
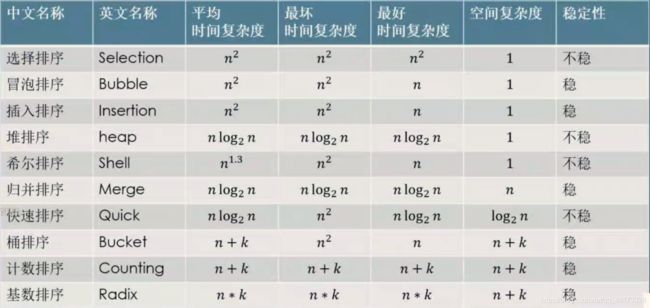
算法的优劣
- 时间维度
- 空间维度
时间复杂度:就是指时间针对于问题规模的变化而变化的规律
O(1),时间不随问题规模的变化而变化
O(n),时间的变化规律为x=y;
计数排序
桶排序思想中的一种,非比较排序
应用:量大但是范围小(几万个数以上,但是所有的数取值范围小,如0到一千。
算法思想:
如数组int[] arr={1,5,1,5,9,0,5,6,8,3,2,4,4}
这个排序算法需要额外的一个计数数组count[],这个数组中初始值设为0,这个计数数组的长度和arr数组长度一致。
- 先排arr[0]=1,将这个值1放到count[]数组下标为1的位置上,令count[1]的值加1,即count[1]=1;(即值是几,就放到下标为几的位置令计数数组count[]中的值加1)
- 再排arr[1]=5,将这个值5放到count[]数组下标为5的位置上,令count[5]的值加1,即count[5]=1;
- 再排arr[2]=1,将这个值1放到count[]数组下标为1的位置上,令count[1]的值加1,因为第1步已经加过一次1了,所以这里是count[1]+1=2;
- 再排arr[3]=5,将这个值5放到count[]数组下标为5的位置上,令count[5]的值加1,因为第2步已经加过一次1了,所以这里是count[5]+1=2;
- 再排arr[4]=9,将这个值9放到count[]数组下标为9的位置上,令count[9]的值加1,即count[9]=1;
- 再排arr[5]=0,将这个值0放到count[]数组下标为0的位置上,令count[0]的值加1,即count[0]=1;
- 再排arr[6]=5,将这个值5放到count[]数组下标为5的位置上,令count[5]的值加1,因为第2步和第4步分别已经加过一次1了,所以这里是count[5]+1=3;
- 以此类推:arr[7]=6,count[6]=1;
- arr[8]=8,count[8]=1;
- arr[9]=3,count[3]=1;
- arr[10]=2,count[6]=1;
- arr[11]=4,count[4]=1;
- arr[12]=4,count[4]=2;(因为第12步已经加过一次1了)
- —————————分割线———————————
- 得到:count[0]=1,count[1]=2,count[3]=1,count[4]=2,count[5]=3,count[8]=1,count[9]=1;(count[2],count[6],和count[10-12]都是0,为啥是0,因为arr数组里没有值为2,6,和值为10-12的)
- 然后对count数组进行输出;
- count[0]=1,相当于arr数组0出现1次,count[1]=2,相当于arr数组1出现2次,………,count[5]=3,相当于arr数组5出现3次,count[8]=1,相当于arr数组8出现1次,count[9]=1,相当于arr数组9出现1次
- 也就是{0,1,1,3,4,4,5,5,5,8,9}
可以发现,出现负数,就会出问题。
计数排序最好直接应用于非负整数的排序中,如果需要排序的数据含有负数,或者是其他类型的值,那么,还需要在不改变相对大小的情况下映射成非负整数,使整个排序逻辑变得复杂。
当然,计数排序也可以排序负数,但是数量特别的大的情乱下,不推荐改变排序逻辑使其支持负数。
下面程序支持了负数
for(int s : source){
//解决出现负数的情况
helper[s - min]++;
}
数组中每个数的取值范围在[200,750]内,完全没必要给count数组分配count[0]—count[199]
如何解决呢?
public class Counting {
/**
* 思路:开辟新的空间,空间大小为max(source)-min(source)+1
* 扫描source,将value作为辅助空间的下标,用辅助空间的该位置元素记录value的个数
* 如:9 7 5 3 1 ,helper=arr(10)
* 一次扫描,value为9,将helper[9]++,value为7,将helper[7]++……
* 如此这般之后,我们遍历helper,如果该位(index)的值为0,说明index不曾在source中出现
* 如果该位(index)的值为1,说明index在source中出现了1次,为2自然是出现了2次
* 遍历helper就能将source修复为升序排列
*/
public static int[] sort(int[] source){
//找到目标数组中的最大值,最小值,用来确定辅助数组空间大小
int max = findMaxElement(source);
int min = findMinElement(source);
//创建辅助空间,helper 数组中,指针存的source的值,元素为目标数组值的个数
int[] helper = new int[max-min+1];
//将source数组中的值填到helper 数组中
for(int s : source){
//解决出现负数的情况
helper[s - min]++;
}
int current = 0;
//扫描helper 数组,将数组回填
for(int i = 0; i < helper.length;i++){
while (helper[i] > 0){
source[current++] = i + min;
helper[i] --;
}
}
return source;
}
private static int findMaxElement(int[] array) {
int max = array[0];
for (int val : array) {
if (val > max)
max = val;
}
return max;
}
private static int findMinElement(int[] array) {
int min = array[0];
for (int val : array) {
if (val < min)
min = val;
}
return min;
}
public static void main(String[] args) {
int[] arr = {
-1,-2,-5,-2,1,5,9,6,3,4,5};
System.out.println(Arrays.toString(sort(arr))); //[-5, -2, -2, -1, 1, 3, 4, 5, 5, 6, 9]
}
}
————————————————
版权声明:本文为CSDN博主「小盒的_1028」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/weixin_44491927/article/details/105120985
给数组增加一个太大的数:1000000000,就会发生内存泄露问题
基数排序
桶排序思想中的一种,非比较排序,多关键字排序
跟计数排序相似:
[1024,258,639,859,2002,63,1]
先千位,在百位,再十位,再个数
对每位采用计数排序。
如:千位:1 0 0 0 2 0 0;使用计数排序;
百位:0 2 6 8 0 0 0;使用计数排序;
然后十位,个位;
就能得出最后结果了。
下面的代码只能用来排正数
public class RadixSort {
public static void sort(int[] number, int d) //d表示最大的数有多少位
{
int k = 0;
int n = 1;
int m = 1; //控制键值排序依据在哪一位
int[][] temp = new int[10][number.length]; //数组的第一维表示可能的余数0-9
int[] order = new int[10]; //数组order[i]用来表示该位是i的数的个数
while (m <= d) {
for (int i = 0; i < number.length; i++) {
int lsd = ((number[i] / n) % 10);
temp[lsd][order[lsd]] = number[i];
order[lsd]++;
}
for (int i = 0; i < 10; i++) {
if (order[i] != 0)
for (int j = 0; j < order[i]; j++) {
number[k] = temp[i][j];
k++;
}
order[i] = 0;
}
n *= 10;
k = 0;
m++;
}
}
private static int findMaxElement(int[] array) {
int max = array[0];
for (int val : array) {
if (val > max)
max = val;
}
return max;
}
public static void main(String[] args) {
int[] data =
{
73, 22, 93, 43, 55, 14, 28, 65, 39, 81, 33, 100, 1000, 100001, 10000};
int max = findMaxElement(data);
String s = Integer.toString(max);
RadixSort.sort(data, s.length());//s.lenth代表最大的数有几位
for (int i = 0; i < data.length; i++) {
System.out.print(data[i] + " ");
}
}
}
优化:可以使用链表
桶排序
数组:{0,9,2,3,5,6,7,4,8,1,10}
- 首先:遍历出最大值10,最小值0;
- 在[0,10]这个范围内,分成若干个桶(几个都行);
- (需要注意的是,这几个桶如果用数组存储内容,则每个桶数组的长度都要是原数组的长度,空间浪费太多;如果用ArrayList则扩充时要经历拷贝数组再扩容等操作,很浪费时间;如果用的是链表,那么他的查询就会变得十分麻烦,所以桶排序很少有人用)
- 我在这把[0,10]分成4个桶:分别是:[0,2.5),[2.5,5),[5,7.5),[7.5,10];
- 然后遍历所有的数组中的数;判断数组中的数分别属于哪个桶,如0,2,1属于[0.2.5]这个桶;9,8,10属于[7.5,10]这个桶;
- 分好之后,每个桶内数据还要再进行排序:桶内排序方法可以是上述排序方法之一
选择排序
时间复杂度O(n²),且不稳定
最简单但是最没用的排序算法,也有优化空间
-
如何计算时间和空间复杂度
-
算法的验证-随机数据生成器、对数器写算法程序的哲学
把 数组[5,4,3,2,0,1] 从小到大排序
第1遍:找出其中最小的数,即0,让他和第一个数调换位置,变成了 [0,4,3,2,5,1],0固定位置,不再比较;
第2遍:找出另外其他几个数中最小的数,即1,让他和第二个数调换位置,变成了 [0,1,3,2,5,4]
第3遍:找出除了0和1,数组中最小的数,即2,让他和第三个数调换位置,变成了 [0,1,2,3,5,4]
第4遍:找出除了0,1和2,数组中最小的数,即3,让他和第四个数调换位置,变成了 [0,1,2,3,5,4]
以此类推。
public class Selection {
public static void main(String[] args) {
int[] arr = {5,6,9,8,6,3,5,3,2,1,0,-1};
//这里减一是因为最后一个数不用排,当然不减一也行
for (int i = 0; i < arr.length - 1; i++) {
int minPos = i;//minPos代表最小的数
for (int j = i+1; j < arr.length; j++) {
if (arr[j] < arr[minPos]) {
minPos = j;
}
}
int temp = arr[i];
arr[i] = arr[minPos];
arr[minPos] = temp;
System.out.println();
System.out.println("经过第"+(i+1)+"次循环后,数组的内容为:");
for (int k = 0; k < arr.length; k++) {
System.out.print(arr[k]+"\t");
}
}
}
}
输出结果:
经过第1次循环后,数组的内容为:
-1 6 9 8 6 3 5 3 2 1 0 5
经过第2次循环后,数组的内容为:
-1 0 9 8 6 3 5 3 2 1 6 5
经过第3次循环后,数组的内容为:
-1 0 1 8 6 3 5 3 2 9 6 5
经过第4次循环后,数组的内容为:
-1 0 1 2 6 3 5 3 8 9 6 5
经过第5次循环后,数组的内容为:
-1 0 1 2 3 6 5 3 8 9 6 5
经过第6次循环后,数组的内容为:
-1 0 1 2 3 3 5 6 8 9 6 5
经过第7次循环后,数组的内容为:
-1 0 1 2 3 3 5 6 8 9 6 5
经过第8次循环后,数组的内容为:
-1 0 1 2 3 3 5 5 8 9 6 6
经过第9次循环后,数组的内容为:
-1 0 1 2 3 3 5 5 6 9 8 6
经过第10次循环后,数组的内容为:
-1 0 1 2 3 3 5 5 6 6 8 9
经过第11次循环后,数组的内容为:
-1 0 1 2 3 3 5 5 6 6 8 9
优化1:是否可以在寻找最小值的时候,顺便可以寻找最大的数,这样时间就会减少一半
优化2:是否可以先arr[1]和arr[2]作比较后,再和arr[0]比较,以此类推
最好/最坏/平均时间复杂度太高O(n²),空间复杂度O(1),主要的坏处在于它复杂度太高同时不稳定
不稳定的原因:例如[5,3,5,8,2,2,1],你很快就会发现前一个5排到了第二个5的后面
可以将println和排序算法提取出来
public class Selection {
public static void main(String[] args) {
int[] arr = {5,6,9,8,6,3,5,3,2,1,0,-1};
//这里减一是因为最后一个数不用排,当然不减一也行
for (int i = 0; i < arr.length - 1; i++) {
int minPos = i;
for (int j = i+1; j < arr.length; j++) {
if (arr[j] < arr[minPos]) {
minPos = j;
}
}
swap(arr, i, minPos);
System.out.println();
System.out.println("经过第"+(i+1)+"次循环后,数组的内容为:");
print(arr);
}
}
static void swap(int[] arr, int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
static void print(int[] arr){
for (int k = 0; k < arr.length; k++) {
System.out.print(arr[k]+"\t");
}
}
}
冒泡算法
比较相邻的元素。
-
如果第一个比第二个大,就交换它们两个对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
-
针对所有的元素重复以上的步骤,除了最后一个;
然后在对第二个数进行第一步的操作;
public class Bubble {
public static void main(String[] args) {
int[] arr = {
5,6,9,8,6,3,5,3,2,1,0,-1};
sort(arr);
print(arr);
}
static void sort(int[] arr) {
for (int i = arr.length-1; i > 0; i--) {
for (int j = 0; j < arr.length - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr,j,j+1);
}
}
}
}
static void swap(int[] arr, int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
static void print(int[] arr){
for (int k = 0; k < arr.length; k++) {
System.out.print(arr[k]+"\t");
}
}
}
插入排序
对于基本有序的数组最好用,稳定
对于数组arr = {9,6,1,3,5},从小到大排
第一遍:对第二个数6,将它在9前面插入,即将9和6交换位置。arr[0]=6,arr[1]=9;–>{6,9,1,3,5}
第二遍:对第三个数1插入到6前面,即1先和9交换位置–>{6,1,9,3,5},1再和6交换位置–>{1,6,9,3,5}
第三遍:将第四个数3插入到1后面,6的前面,即6和9的索引各自+1,3的索引-2。变成{1,3,6,9,5}
第四遍:将第五个数5插入到3后面,6的前面,即6和9的索引各自+1,5的索引-2。变成{1,3,5,6,9}
在什么位置插入主要取决于插入位置,插入位置前面的数要比这个数小,这个数插入的位置后面的数要比这个数大;
public class Insertion {
public static void main(String[] args) {
int[] arr = {5,6,9,8,6,3,5,3,2,1,0,-1};
sort(arr);
print(arr);
}
static void sort(int[] arr){
for (int i = 1; i < arr.length; i++) {
for (int j = i; j > 0; j--) {
if (arr[j] < arr[j-1]){
swap(arr, j, j-1);
}
}
}
}
static void swap(int[] arr, int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
static void print(int[] arr){
for (int i : arr) {
System.out.print(i + "\t");
}
}
}
优化:用临时变量记录标记项,去掉swap方法
简单排序算法:
- 冒泡,基本不用,太慢
- 选择,基本不用,不稳
- 插入排序,样本小且基本有序的时候效率比较高
希尔排序
1959年Shell发现的,是改进的插入排序
因为不稳定,所以用处不太大
算法思想:
给定一个间隔(在这里先假设为4,后面会讲)
数组arr={5,6,9,8,6,12,7,3,2,1,0,-1}
5——6——9——8——6——12——7——3——2——1——0——-1
-
对5间隔为4,得到5——12——1(5跟12间隔四个数,12跟1间隔四个数),对5,12,1进行插入排序,即1——5——12,即1,6,9,8,6,1,7,3,2,12,0,-1
-
对6间隔为4,得到6——7—— -1,插入排序:-1——6——7,即1,6,9,8,-1,1,6,3,2,12,0,7
-
以此类推,对9,8,6间隔为4,排序。
最后得到的数组不有序,但是前面的数大多数数小,后面的大多数数大
缩小间隔,当间隔为2
进行如上1,2,3操作
再缩小间隔,间隔为1。无论怎样,最后都要进行间隔为1的排序
public class Shell {
public static void main(String[] args) {
int[] arr = {
5, 6, 9, 8, 6, 3, 5, 3, 2, 1, 0, -1, -99};
sort(arr);
print(arr);
}
static void sort(int[] arr) {
//这里用了Knuth序列
int h = 1;
while (h <= arr.length / 3) {
h = h * 3 + 1;
}
for (int gap = h; gap > 0; gap = (gap - 1) / 3) {
for (int i = gap; i < arr.length; i++) {
for (int j = i; j > gap - 1; j -= gap) {
if (arr[j] < arr[j - gap]) {
swap(arr, j, j - gap);
}
}
}
}
}
static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
static void print(int[] arr) {
for (int i : arr) {
System.out.print(i + "\t");
}
}
}
归并排序
递归:
public class Merge {
public static void main(String[] args) {
System.out.println(f(10));
}
private static long f(int i) {
//递归一定要有一个暂停的办法
if (i<1){
return -1;
}
if (i == 1){
return 1;
}
return i+f(i-1);
}
}
算法思想:
对一个数组进行归并–>即{1,5,6,9,8,5,3}
- 把一个数组分成一半–>{1,5,6}__{9,8,5,3}
- 再把两个一半分为一半{1,5}{6}__{9,8}{5,3}
- 直到把数组分成只剩两个数或一个数,不能再分割为止,剩下两个数,对这两个数排序。然后对上一次分割成的两个数组进行排序
- 在分割过程中,如果分后的某个数组已经是一个从小到大的数组,就不再进行分割
public class Merge {
public static void main(String[] args) {
System.out.println(f(10));
int[] arr = {5, 6, 9, 8, 6, 3, 5, 3, 2, 1, 0, -1, -99};
sort(arr,0,arr.length-1);
print(arr);
}
static void sort(int[] arr,int leftPtr, int rightPtr){
if (leftPtr == rightPtr) return;
//分成两半
int mid = leftPtr + (rightPtr-leftPtr)/2;
//左边排序
sort(arr, leftPtr, mid);
//右边排序
sort(arr, mid+1, rightPtr);
merge(arr,leftPtr,mid+1, rightPtr);
}
static void merge(int[] arr, int leftPtr, int rightPtr,int rightBound){
int mid = rightPtr - 1;
int[] temp = new int[rightBound - leftPtr + 1];
int i = leftPtr;//左指针
int j = rightPtr;//右指针
int k = 0;
while (i <= mid && j <= rightBound){
if (arr[i] <= arr[j]){
temp[k] = arr[i];
i++;
k++;
}else{
//可以写成temp[k++] = arr[j++];
temp[k] = arr[j];
j++;
k++;
}
}
while (i<=mid) temp[k++] = arr[i++];
while (j<=rightBound) temp[k++] = arr[j++];
for (int l = 0; l < temp.length; l++) {
arr[leftPtr + l] = temp[l];
}
}
static void swap(int[] arr, int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
static void print(int[] arr){
for (int i : arr) {
System.out.print(i + "\t");
}
}
//递归
private static long f(int i) {
if (i<1){
return -1;
}
if (i == 1){
return 1;
}
return i+f(i-1);
}
}
对象排序一般要求稳定,应用十分广泛
快速排序
算法思想
如:arr={1,5,4,0,-1,5}
-
取数组长度/2的中间值,即arr[2]=4;(可以随便取一个数,不一定非在中间取)
-
把比4小的放左边,即0和-1要放在左边;
- 先排0,0比arr[0]=1小,则把0放在arr[0]前头,[0,1,5,4,-1,5];
- 再排-1,-1比arr[0]=0小,则把0放在arr[0]前头,[-1,0,1,5,4,5];
-
这时,数组已经变成[-1,0,1,5,4,5],把比4大的放右边,即4前面的那个5,这个5和和4后面的5做比较,如果前面的5大于等于后面那个5,就把前面那个5换到现在这个5的后面,[-1,0,1,4,5,5];
/**
* @Author Z
* @Date 2021/3/21 14:28
*/
public class QuickSort {
public static void main(String[] args) {
int[] arr = {
-101,5, 6, 9, 8, 6, 3, 5, 3, 2, 1, 0, -1,-99,100, (int)( Math.random()*100)};
sort(arr, 0, arr.length - 1);
print(arr);
}
static void sort(int[] arr, int leftBound, int rightBound) {
if (leftBound >= rightBound) return;
int mid = partition(arr, leftBound, rightBound);
sort(arr, leftBound, mid-1);
sort(arr, mid+1,rightBound);
}
static int partition(int[] arr, int leftBound, int rightBound) {
int pivot = arr[rightBound];
int left = leftBound;
int right = rightBound - 1;
while (left <= right) {
while (left <= right && arr[left] <= pivot) {
left++;
}
while (left <= right && arr[right] > pivot) {
right--;
}
if (left < right) {
swap(arr, left, right);
}
}
swap(arr, left, rightBound);
return left;
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
static void print(int[] arr) {
for (int i : arr) {
System.out.print(i + "\t");
}
}
}