对音频信号作短时傅里叶变换（STFT）/小波变换处理（python + matlab）

对音频信号作短时傅里叶变换（STFT）处理，并绘制语谱图

摘要：录制一段音频，分别在matlab，python两种环境下，对其作短时傅里叶变换（STFT），最终得到期望的语谱图。

一、前言

1. 基础概念：
在对音频信号进行分析处理前，先简要回顾一下所用到的分析函数傅里叶变换的相关知识。

• 什么是傅里叶变换？
  傅里叶的基本定义与性质在这里就不作赘述了，文章主要想说明它的主要应用，以助于大家对这个概念有一个更为形象的认识。（傅里叶基础概念与性质，推荐观看b站李永乐的讲解，文末附视频链接）
  

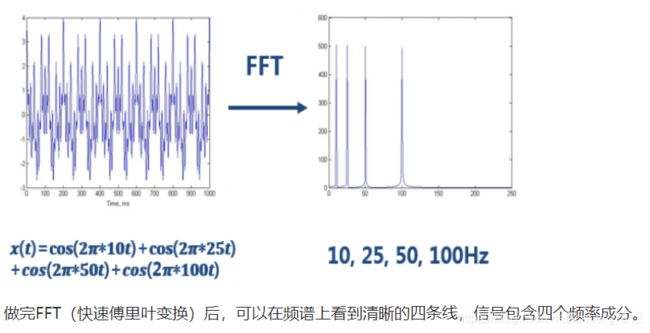
• 傅里叶变换是一种分析信号的方法，它可分析信号的成分，也可用这些成分合成信号。在分析信号时，主要应用于处理平稳信号，通过傅里叶变换可以获取一段信号总体上包含哪些频率的成分，但是对各成分出现的时刻无法得知。

• 因此对于非平稳信号，傅里叶变换就显示出了它的局限性，而我们日常生活中的绝大多数音频都是非平稳信号的。而解决这一问题的方法，就是采用短时傅里叶变换或者小波变换，对信号进行处理。

• 什么是短时傅里叶变换？
  
  短时傅里叶变换（STFT）的核心思想：“加窗”，即把整个时域过程分解成无数个等长的小过程，每个小过程近似平稳，再对每个小过程进行傅里叶变换（FFT）。尽管STFT可以处理非平稳信号，但是它仍然有其局限性，即对窗函数的宽窄无法做到精确定义。
  
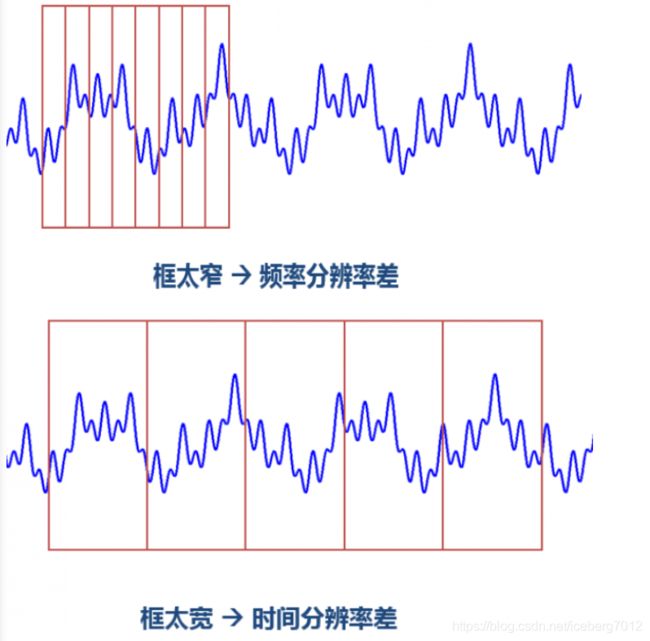
  窗函数选择太窄，窗内的信号太短，会导致频率的分析不够精准，频率分辨率差；窗选的太宽，时域上又不够精细，时间分辨率低

• 傅里叶与短时傅里叶的联系与区别？
  

• 什么是小波变换？

  小波变换的核心思想：“把傅里叶变换的无限长三角函数的基换成有限长的会衰减的小波基”，这样不仅可以获取频率，还可以定位时间。更为详细的介绍可以参考本段末附上的参考来源，查询大佬相关阐述。

本文参考来源：
https://rf.eefocus.com/article/id-xiaobobianhuan?p=1 傅里叶–短时傅里叶–小波分析
https://blog.csdn.net/daaikuaichuan/article/details/80781505 小波与短时傅里叶的区别
https://wenku.baidu.com/view/4b9bb22c30b765ce0508763231126edb6f1a768e.html?fr=search-1_income7 短时傅里叶的概念理解

• 什么是语谱图？

  语谱图：时间依赖于傅里叶分析的显示图形，实际上是一种动态频谱，综合了频谱图和时域波形图的优点，明显地显示出语音频谱随时间的变化情况。（其中，纵轴为频率，横着为时间，任一给定频率成分在给定时刻的强弱，用点的黑白度来表示）

2. 概念的形象化理解：

• 短时傅里叶变换进行音频分析流程的直观理解
  
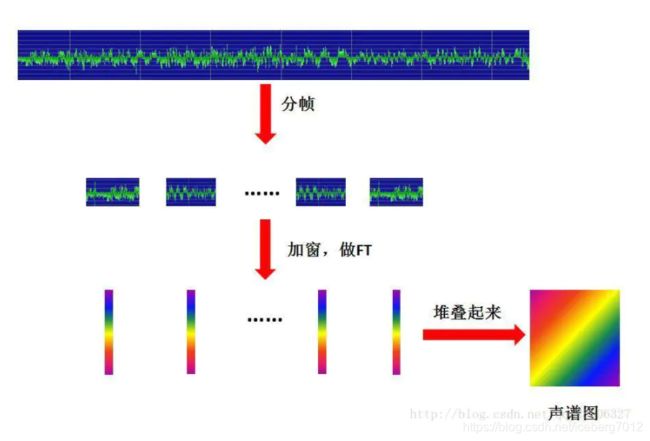
• 欧拉公式可以将任意函数转化为一系列正（余）弦函数之和。任意函数在这里指我们的时域信号，而正（余）弦函数包含信号的频率和对应振幅信息。（时域处理）
• 傅立叶变换可以将时间0～t内采集的信号（时域，横轴时间、纵轴大小）分解为不同频率上的信号分量（频域，横轴频率、纵轴大小）。
• 短时傅立叶采用滑动窗口机制，设定窗口大小和步长，让窗口在时域信号上滑动，分别计算每个窗口的傅立叶变换，形成了不同时间窗口对应的频域信号，拼接起来就成为了频率随时间变化的数据（时频信号，数据绘图得语谱图）

文章参考来源：
https://www.jianshu.com/p/7e160442830f 直观理解短时傅里叶变换 STFT（简书）
https://www.bilibili.com/video/BV1A4411Y7vj/?spm_id_from=333.788.videocard.1 傅里叶变换-李永乐（b站视频，讲的很好）

3. 思路流程：

编程思路：

短时傅里叶变换（STFT）就是先把一个函数和窗函数进行相乘，然后再进行一维的傅里叶变换。并通过窗函数的滑动得到一系列的傅里叶变换结果，将这些结果排开便得到一个二维的表象。具体而言，可分为如下几步（以matlab源码为例）：
（1）读取音频文件。（调用audioread，处理得到一个保存音频数据的数组，和一个采样频率）
（2）确定相关参数。（如窗函数、窗长、重叠点数，重叠长度，傅里叶点数等）
（3）调用spectrogram函数，做短时傅里叶变换。（S-将输入信号做STFT处理后得到的二维含时间、频率序列的数组数据；更为详细的处理过程见spectrogram函数定义）
（4）根据处理后的时频矩阵，绘制语谱图.

文章参考来源：
https://blog.csdn.net/zhaoyinhui0802/article/details/53048362 短时傅里叶变换原理解

整体思路：

• 录制一段音频或寻找一段音频（.MP3/.m4a）,通过文件格式转换为.wav文件（网上有在线转换的方式，文后会给出网址链接），在python（调用librosa函数）或者matlab（调用audioread，spectogram函数）中对文件进行处理（STFT变换），最后对处理后的信号作绘图输出，得到语谱图。

文章参考来源：
https://cn.office-converter.com/ 文件在线转换网址

4. 必要准备：

   音频文件+python应用环境+matlab应用环境

python应用环境：

• 作者是在vscode中编写python代码，CSDN中有许多博主介绍了vscode使用python的方法，在这里不做多的赘述，文章用到的调用函数为librosa，文章后面会贴出librosa库安装的说明。

• 可通过pip list 或 conda list 查询python 或anaconda是否包含librosa 库文件

文章参考来源：
https://blog.csdn.net/Small_Yogurt/article/details/104964760 vscode安装教程
https://blog.csdn.net/qq_40197828/article/details/93468787 vscode中配置python环境（可以选择配置anaconda中的python，这样会减少后续代码实现阶段，函数库的安装，如numpy,librosa等）
https://blog.csdn.net/u010824101/article/details/85239223 Windows10中用Anaconda的conda环境和VSCode工具来编写python代码
https://blog.csdn.net/zzc15806/article/details/79603994 音频处理库—librosa的安装与使用

matlab应用环境：

• 如何安装以及破解matlab，请参考下方资料来源（大佬写的非常详细），这里不作赘述了。

  安装前须知（提醒）：

  1.安装全程须断开网络，否则破解不成功；

  2.解压和安装前先关闭360、腾讯管家等杀毒软件，防止误杀破解补丁，导致破解失败；

  3.Matlab 2018b适用于WIN7/8/10（64位）系统，亲测可用！

  4.推荐电脑最低配置：内存8G+，处理器酷睿I5+；

文章参考来源：
https://blog.csdn.net/qq_26900233/article/details/88816789 MATLAB R2018b 安装教程（含软件资源）

二、代码实现

1. python源码：

import librosa
import librosa.display
import matplotlib.pyplot as plt

# 读取音频文件
filepath = 'C:\\Users\\非黑不即白\\Desktop\\Audio_processing_STFT\\python_project\\data\\'
filename = filepath + 'test_digital.wav'
x, sr = librosa.load(filename, sr=None)  # x--音频时间序列(一维数组) ； sr--音频的采样率

# STFT处理绘制声谱图
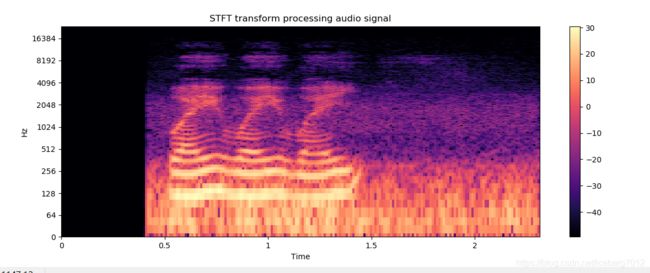
X = librosa.stft(x)
Xdb = librosa.amplitude_to_db(abs(X))  # X--二维数组数据

plt.figure(figsize=(14, 5))
librosa.display.specshow(Xdb, sr=sr, x_axis='time', y_axis='log')
plt.colorbar()
plt.title('STFT transform processing audio signal')
plt.show()

2. matlab源码：

[X, Fs]=audioread('C:\Users\非黑不即白\Desktop\Audio_processing_STFT\matlab_project\test_digital.wav');   % Fs 采样率 48000
                 % audioread函数读取音频文件（X--保存音频信号的数据；Fs--音频采样率）
                  
figure;       % 绘图
win_sz = 128;       % 窗函数长度设置为128
han_win = hanning(win_sz);        % 选择海明窗
nfft = 2^nextpow2(length(han_win));       % DFT点数（通常取最接近信号长度的2的整数次幂，即 nfft = 2^nextpow2(length(window)) ）=128=win_size
nooverlap = win_sz - 1;        % 重叠长度（而随着noverlap参数的引入，增大了时间轴分辨率，即每隔（Nw - noverlap）长度进行一次频率轴的更新，随着noverlap逐渐接近Nw，图像上表现为时间轴更加“细腻”，但随之而来的肯定是计算次数的增加。）
[S, F, T, P] = spectrogram(X(:,1), window, nooverlap, nfft, Fs);   
                % spectrogram注释：x：输入的信号 向量；window：窗口长度 该函数默认使用海明窗；noverlap：各段之间重叠的采样点数 即两窗口相重叠的部分；nfft：对窗口下的信号做FFT的点数；fs：信号的采样率
                               % s：输入信号x的短时傅里叶变换。（它的每一列包含一个短期局部时间的频率成分估计，时间沿列增加，频率沿行增加。）
                               % F：为四舍五入的频率，其长度等于S的行数。
                               % T：频谱图计算的时刻点，值为窗的时刻中值。
                               % P：功率谱密度PSD(Power Spectral Density) 

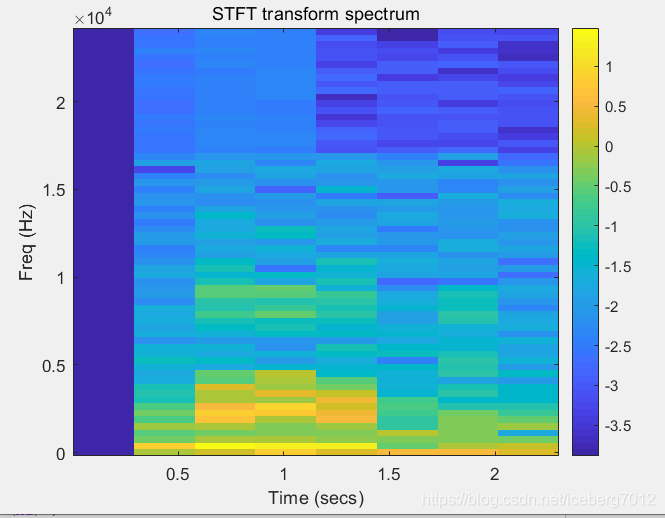
imagesc(T, F, log10(abs(S)))   % 绘图函数（将矩阵S中的元素数值按大小转化为不同颜色，并在坐标轴对应位置处以这种颜色染色；T、F为其横纵坐标）
colorbar；
set(gca, 'YDir', 'normal')     % 坐标轴设置（ydir表示Y轴；normal-坐标轴正序；reverse--倒序）
xlabel('Time (secs)')
ylabel('Freq (Hz)')
title('STFT transform spectrum')

3. 小波变换处理（matlab）:

[X, Fs]=audioread('C:\Users\非黑不即白\Desktop\Audio_processing_STFT\matlab_project\test_digital.wav');   % Fs 采样率 48000
                  % audioread函数读取音频文件（X--保存音频信号的数据；Fs--音频采样率）

wavename='cmor3-3'; % 选定小波基                
totalscal=256;
Fc=centfrq(wavename); % 小波的中心频率  测得Fc = 3
c=2*Fc*totalscal;    % 测得c = 1536
scals=c./(1:totalscal);   % 求得尺度
f=scal2frq(scals,wavename,1/Fs); % 将尺度转换为频率   % 频率在0-500Hz取1024个点
coefs = cwt(X(:,1),scals,wavename); % 求连续小波系数
t=0:1/Fs:size(X(:,1))/Fs;
figure
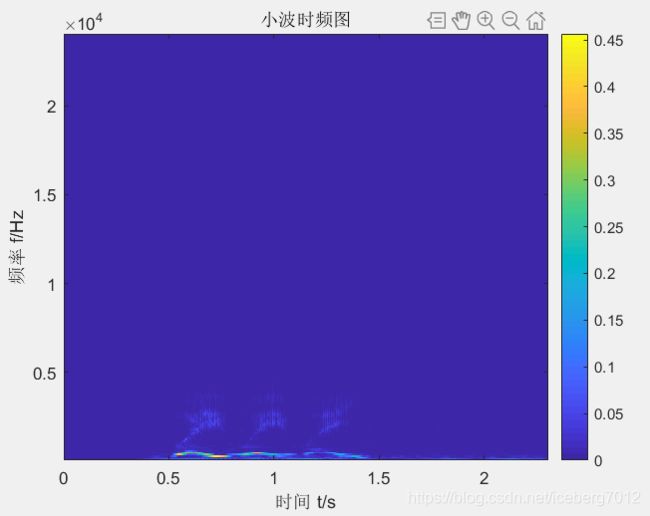
imagesc(t,f,abs(coefs));
set(gca,'YDir','normal')
colorbar;
xlabel('时间 t/s');
ylabel('频率 f/Hz');
title('小波时频图')

文章参考来源：
https://blog.csdn.net/lanchunhui/article/details/72240693 matlab 时频分析（短时傅里叶变换、STFT）
https://blog.csdn.net/weixin_42765703/article/details/104871604 解析MATLAB短时傅里叶变换函数spectrogram()
https://blog.csdn.net/zb1165048017/article/details/80682473 【音频处理】短时傅里叶变换
https://blog.csdn.net/weixin_44586750/article/details/103219952 数字信号处理——时频分析（短时傅里叶变换+手动实现时频分析）
https://blog.csdn.net/qq_42815385/article/details/89095135 STFT（短时傅里叶变换）音频特征提取，用于语音识别 python
https://blog.csdn.net/Barry_J/article/details/81065932 音频特征提取——python/ librosa工具包使用
https://blog.csdn.net/qq_34218078/article/details/101255636 librosa语音信号处理
https://blog.csdn.net/yunman2012/article/details/103542690 librosa处理音频信号

三、总结（作者小白话）

• 写这篇博客的缘由，主要想对近期音频信号处理相关知识的学习，做一个系统性的梳理，同时也希望能够对大家有所帮助（学习阶段，查阅了不少大佬文章，收益匪浅，这些都成为我写博客，分享自己的学习历程，与经验教训的一个动力）。
• 整个学习阶段，从了解傅里叶变换，到python、matlab环境的配置和使用，以及后续的音频文件处理，STFT变换等，走过了许多弯路，也遇到了一些不常见的bug（主要是python环境配置，库安装时），但最终还是坚持了下来。目前对音频处理的相关学习还不是很深入，文章还存在许多不全面的地方，在后续深入学习过程中，会对不合理的地方做出调整，也希望各位大佬能多多指教。相互学习，共同进步啊，哈哈哈。（文章引用了一些大佬的文章（文章小节处有标注），以便各位同仁能更全面的了解，当然也会存在一些疏漏，请指教，望见谅。）
• 补充，写文章阶段时，发现了一位大佬关于python语音基础操作的文章，内容很详实，包含音频生成，语音分析、处理的介绍，收益匪浅，文章最后附原文链接，希望有助于大家理解语音信号处理。

文章参考来源：
https://blog.csdn.net/sinat_18131557/article/details/106440757 Python语音基础操作（对python处理语音信号的过程介绍的很详细，推荐！）