基于Amos路径分析的输出结果参数详解
基于Amos路径分析的输出结果参数详解
- 1 Output path diagram
- 2 Amos Output
-
- 2.1 Analysis Summary
- 2.2 Notes for Group
- 2.3 Variable Summary
- 2.4 Parameter Summary
- 2.5 Assessment of normality
- 2.6 Observation farthest from the centroid (Mahalanobis distance)
- 2.7 Sample Moments
- 2.8 Notes for Model
- 2.9 Estimates
- 2.10 Modification Indices
- 2.11 Minimization History
- 2.12 Pairwise Parameter Comparisons
- 2.13 Model Fit
- 2.14 Execution Time
系列文章共有四篇,本文为第二篇,主要由整体层面关注输出结果参数。
博客1:基于Amos的路径分析与模型参数详解
博客3:基于Amos路径分析的模型拟合参数详解
博客4:基于Amos路径分析的模型修正与调整
在博客1(https://blog.csdn.net/zhebushibiaoshifu/article/details/114333349)中,我们详细介绍了基于Amos的路径分析的操作过程与模型参数,同时对部分模型所输出的结果加以一定解释;但由于Amos所输出的各项信息内容非常丰富,因此我们有必要对软件所输出的各类参数加以更为详尽的解读。其中,本文主要对输出的全部参数加以整体性质的介绍,而对于与模型拟合程度相关的模型拟合参数,大家可以在博客3、博客4中查看更详细的解读。
1 Output path diagram
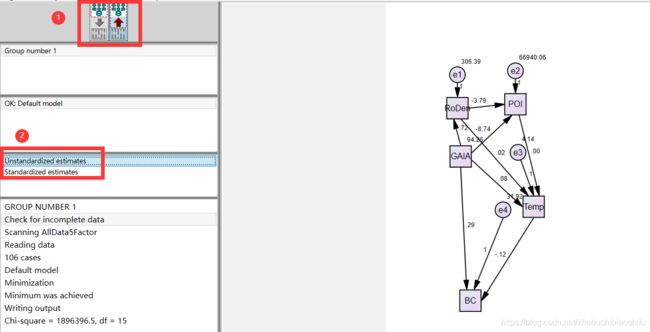
首先,通过上一篇博客,我们已经知道可以在“Output path diagram”模块,对模型的非标准化结果与标准化结果加以显示。如下图,若为非标准化结果,自变量、残差旁的数字代表其方差;而对于标准化结果,箭头旁的数字代表对应回归方程的R方。具体请见这篇博客。
2 Amos Output
点击软件左侧“View Text”按钮,可以查看更为详细的模型结果。
我们就由上到下,依次解释每一个界面的含义。
2.1 Analysis Summary
这里是模型分析的摘要,包括模型运行的时间与标题。
2.2 Notes for Group
这里是对模型的备注。
首先,“The model is recursive.”代表着这一模型是一个递归模型。递归模型,顾名思义是内生变量间因果关系为单方向的结构方程模型;换句话讲,递归模型中任何一个变量,不能既是另一个变量的起因,且又同时是其效应。
其次,“Sample size”则代表了样本个数。

2.3 Variable Summary
这里是对模型中各种变量的总结。
首先,“Observed,endogenous variables”即“观测变量、内生变量”。观测变量就是可以被观测、测量而直接得到的变量(本文中所有土壤属性与对应的环境变量都是已知的,也就是可以直接测量的)。内生变量就是被其它自变量预测的变量,可以认为相当于是一个因变量;但要注意,尽管内生变量多作为因变量,但也可能作为影响他人的自变量,例如本文中的内生变量POI,可以影响Temp,又受到GAIA与RoDen影响。内生变量在Amos中突出的特点即为其被箭头所指,或者说其有一个残差项(这是因为AMOS路径图表示的为线性回归模型,因此所有因变量都需要加上一个残差)。
其次,“Observed,exogenous variables”即“观测变量、外生变量”。外生变量即为不受任何其他变量影响,但影响他人的变量。其在路径图中就是没有被任何一个箭头指到的变量。
再接下来的一栏“Unobserved,exogenous variables”,相信大家都可以看出了,是“非观测变量、外生变量”。非观测变量又叫做潜在变量,是指不能直接进行测量,但可以通过观察变量从而进行大致衡量、测度的变量。那么在本文中,所用的残差就都是非观测变量了。
最后一栏“Variables counts”,就是不同变量的计数。

2.4 Parameter Summary
这里是模型中不同种类的变量摘要。
我们首先看表格的第一行。“Weights”为“回归权重”,我认为就是回归系数;“Covariances”为“协方差”;“Variances”为“方差”;“Means”为“平均值”;“Intercepts”为“截距”。
再看表格的第一列。“Fixed”表示模型中值已经被固定为一个常数的参数;“Labeled”表示模型中值已经带有标签的参数;“Unlabeled”表示模型中既没有被固定值,也没有带上标签的参数,这一类参数可以取任意值(当然,对于Labeled的参数,只要其Label为唯一的,其也可以取任意值)。

2.5 Assessment of normality
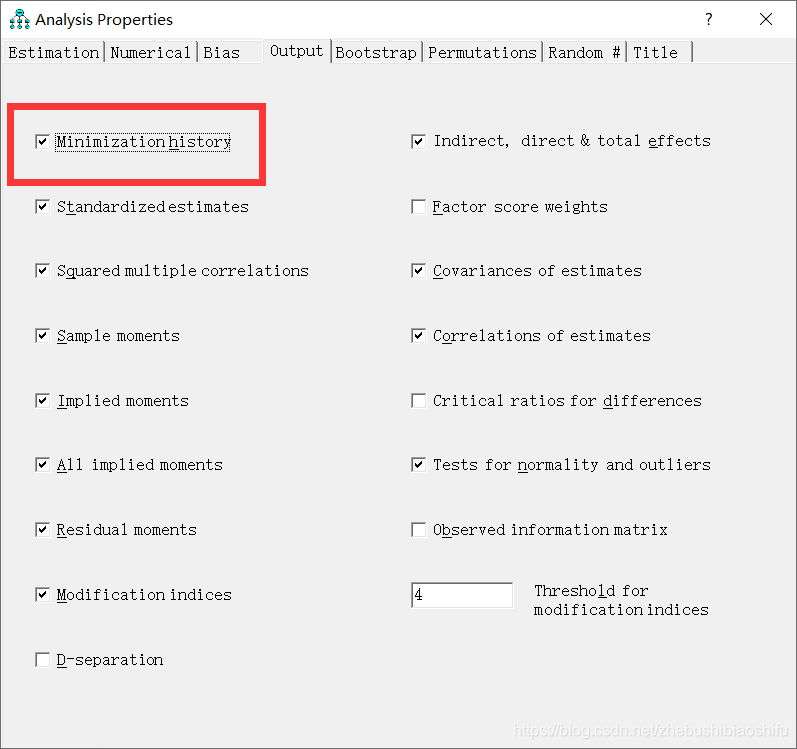
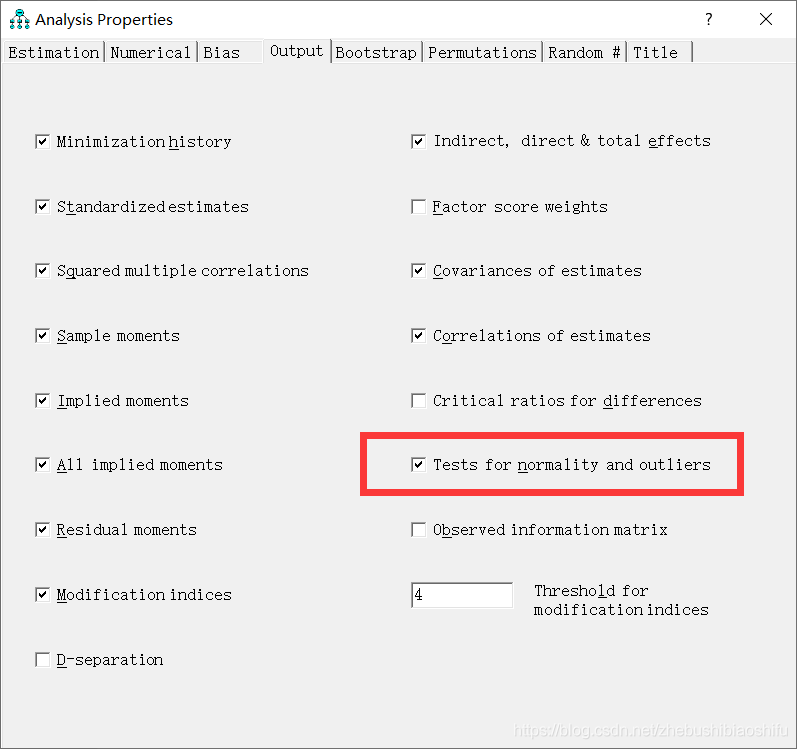
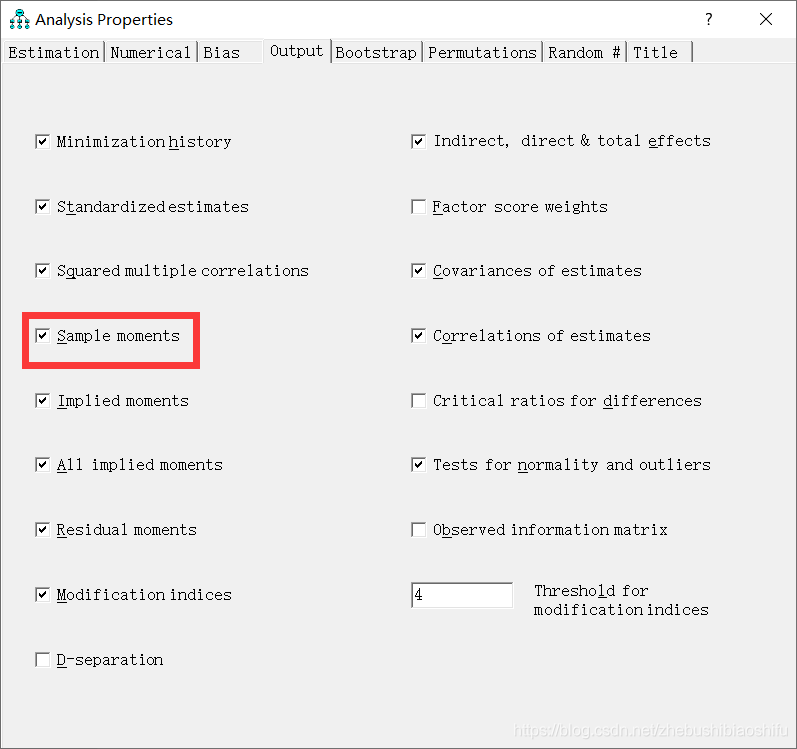
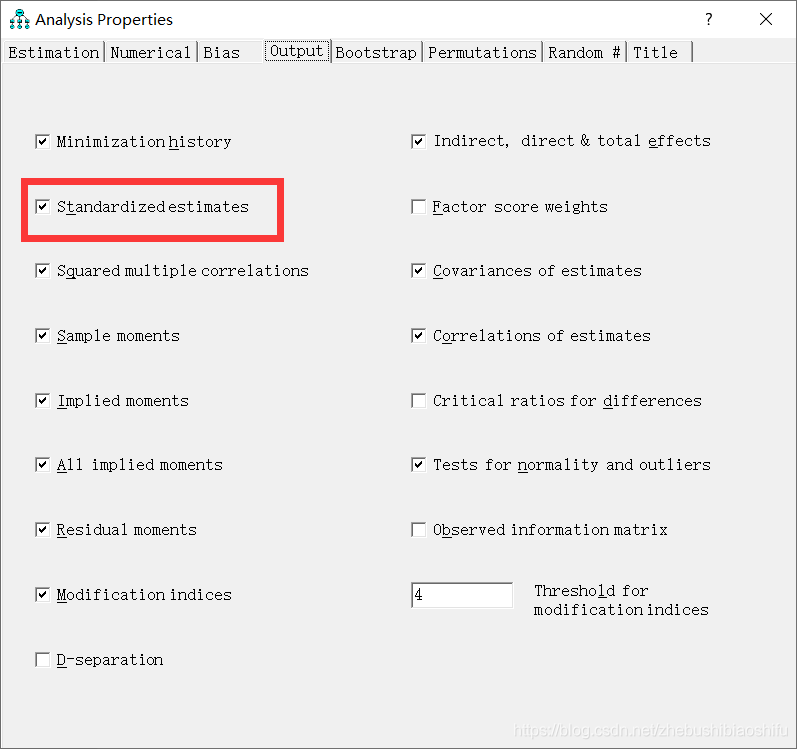
这里是对模型中变量的正态分布检验,对应着当初“Output”中我们勾选的“Test for normality and outliers”选项(如下下图所示)。
我们首先看表格的第一行。“min”与“max”分别代表变量的“最小值”与“最大值”;“skew”为“偏度”(skewness),是统计一组数字非对称程度的度量,数据符合正态分布时为0,右偏分布(正偏分布)时大于0,左偏分布(负偏分布)时小于0;“c.r.”个人认为应该是“C-R下界”;“kurtosis”为“峰度”,表示一组数据在平均值处峰值的高低,峰越尖,峰度越小,峰越厚,峰度越大。
随后,需要注意最后一行“Multivariate”表示“多元变量”。

2.6 Observation farthest from the centroid (Mahalanobis distance)
这里是对模型中变量的异常值检验,同样对应着当初“Output”中我们勾选的“Test for normality and outliers”选项。
表格第一列“Observation number”是每一个异常值对应的数据编号;“Mahalanobis d-squared”可以视作距离的度量,其越大数据越有可能是异常值。

2.7 Sample Moments
这里是样本矩,对应着当初“Output”中我们勾选的“Test for normality and outliers”选项。
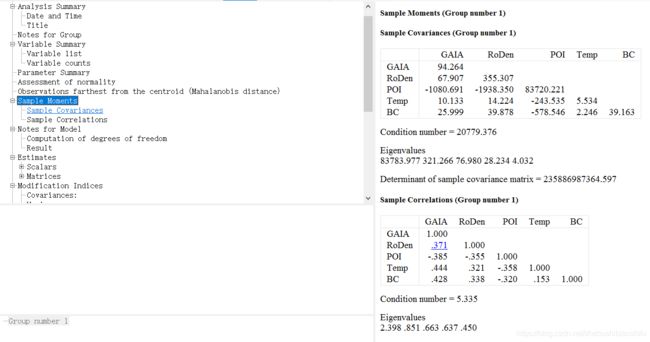
其中,第一个“Sample Covariances”为“样本协方差矩阵”,其具体计算会随当初“Bias”中我们勾选的“Covariances to be analyzed”选项类型而改变。其中,对角线上为样本自身的方差,其余地方为样本之间的协方差。
接下来,第二个“Condition number”为协方差矩阵的“条件编号”,其等于矩阵的最大特征值除以最小特征值。
第三个“Eigenvalues”为协方差矩阵的“特征值”。
第四个“Determinant of sample covariance matrix”为协方差矩阵的“行列式”。在正定协方差矩阵的情况下,行列式接近零表示至少一个观察到的变量几乎线性依赖于其他变量。 其结果取决于指定的模型和差异函数。从数值的角度来看,行列式接近于零可能使得难以估计模型的参数。从统计的角度来看,行列式接近于零可能意味着对某些参数的估计不佳(将显示为较大的估计标准误差)。
第五个“Sample Correlations”表示“样本相关系数矩阵”。其对应着当初“Output”中我们勾选的“Standardized estimates”选项。
第六个“Condition number”表示相关矩阵的“条件编号”,样本相关矩阵的条件编号是其最大特征值除以其最小特征值。
第七个“Eigenvalues”为相关矩阵的“特征值”。
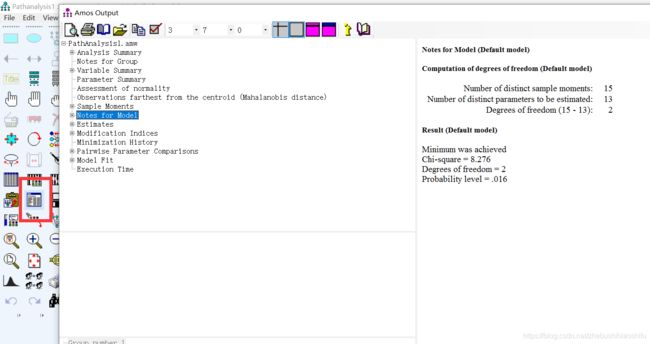
2.8 Notes for Model
这里为模型整体情况的备注,与单个模型有关的消息出现在此处。
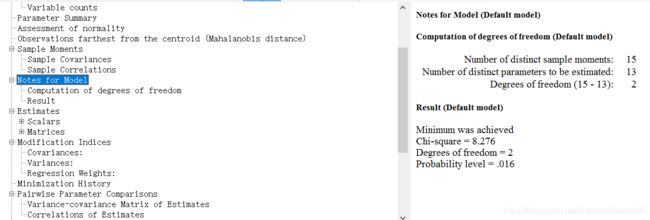
第一个“Computation of degrees of freedom”显示了Amos如何达成当前的自由度结果——自由度即不同样本矩的数量与必须估计的不同参数的数量之间的差异。
第二个“Minimum was achieved”表示模型达到了局部最优解。
接下来两个分别代表着卡方值与自由度。
接下来的“Probability level”表示:如果满足适当的分布假设,且当前模型是正确的,则其值是获得与从当前数据集获得的卡方统计量一样大的卡方统计量的近似概率。例如,如果该值等于或小于0.05,则数据与模型的偏离在0.05级别上是显著的。
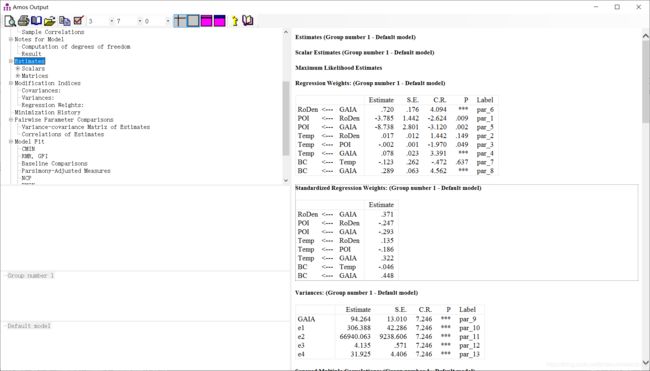
2.9 Estimates
第一个“Scalar Estimates”为“标量估计”。
第二个“Maximum Likelihood Estimates”为“最大似然估计”
接下来,“Regression Weights”为回归系数估计。表格中第一行,“Estimate”为实际估计值;“S.E.”为“近似标准误差”,其不适用于相关性和标准化回归系数,也不适用于ULS或SLS估计方法;“C.R.”为“临界比率”,其是参数估计值除以其标准误差的估计值。如果满足适当的分布假设,则该统计量在参数的总体值为零的零假设下具有标准正态分布。例如,如果某个估计的临界比率大于2(以绝对值计),则该估计在0.05级别与零显著不同。即使没有分布假设,临界比率也具有以下解释:对于任何不受约束的参数,其临界比率的平方大约是在固定该参数固定为零的情况下重复进行分析,卡方统计量将增加的量(其不适用于相关性和标准化回归系数,也不适用于ULS或SLS估计);“P”就是“p值”,若小于0.001就用“***”表示,说明自变量对因变量有显著性影响;“Label”为“标签列”,如果前期已命名参数,则该名称将显示在此列中。我们需要知道参数的名称,以便读取参数之间的协方差、参数之间的相关性以及参数之间差异的临界比率的显示。如有必要,Amos会为我们尚未命名的任何参数命名,且这一名称将与我们提供的名称一起出现在标签列中。
随后,“Standardized Regression Weights”为“标准化回归系数”。
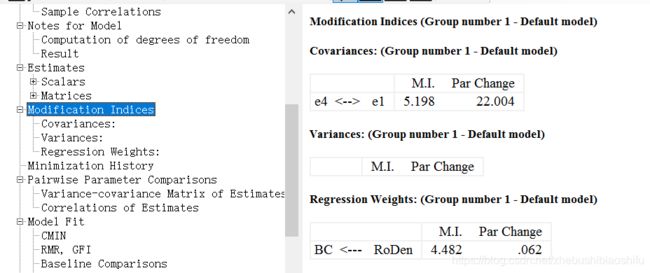
2.10 Modification Indices
“Modification Indices”为“修改索引值”。修改索引大于指定阈值的每个参数将显示在此处,并在标记为的列中显示:
“M.I”:修改索引
“Par Change”:估计参数变化
2.11 Minimization History
“Minimization History”表示每一次迭代中,误差函数的数值。其对应着当初“Output”中我们勾选的“Minimization history”选项。
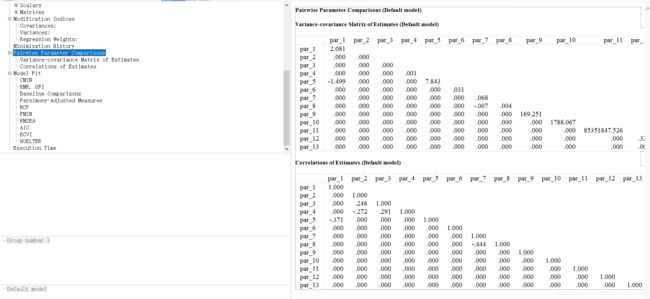
2.12 Pairwise Parameter Comparisons
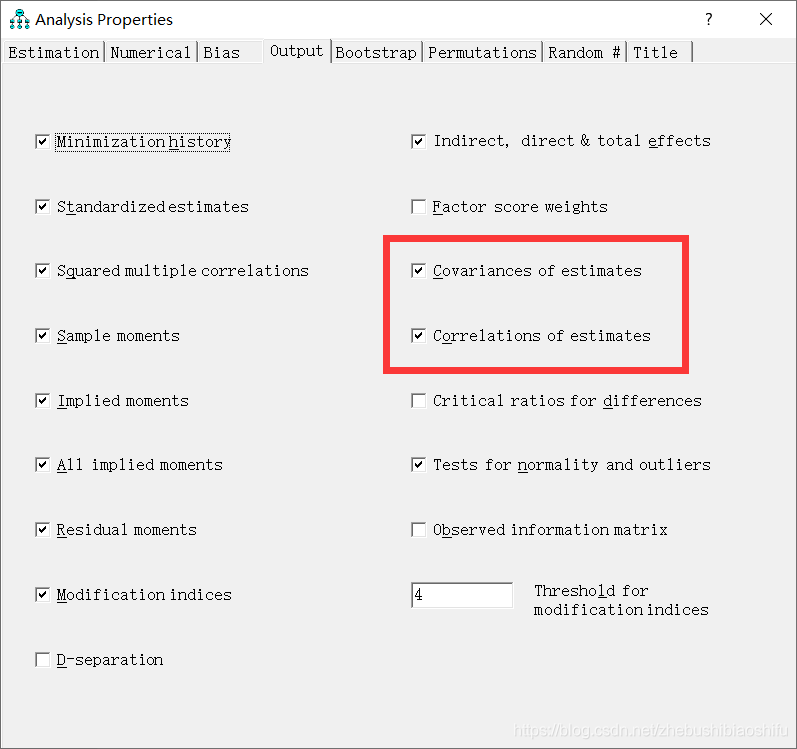
这一模块为模型中全部参数的两两比较,包括方差/协方差与相关系数。其对应着当初“Output”中我们勾选的如下两个选项。
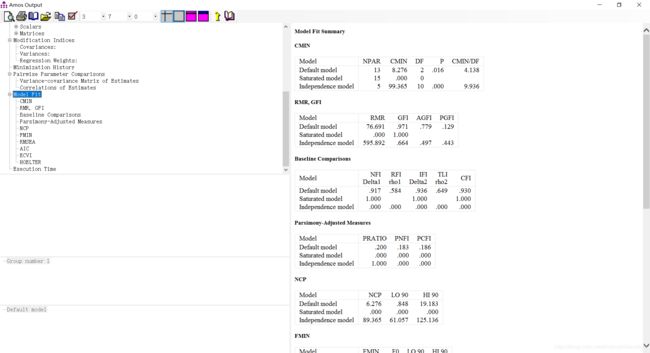
2.13 Model Fit
这一部分为模型整体的拟合情况衡量参数。关于这一部分参数更为细致的介绍请看这篇博客。
2.14 Execution Time
这一模块展示了模型的运行时间。