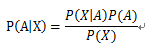一、理论篇
总所周知,概率界分为两大学派,一是频率派,二是贝叶斯派。如果用一句话来陈述它们的核心区别,我倾向于这样讲,“频率派:概率是事件在长时间内发生的频率;贝叶斯派:概率可以解释为我们对一件事情发生的相信程度(信心)。”,通俗来讲,前者需大量的事件,看发生的次数,后者针对某一件事,我们对它发不发生有多大的信心。
这周在学习贝叶斯,正好还看了点吴军的《数学之美》,前几章大多涉及到贝叶斯、马尔科夫链在翻译、语音识别等方向的应用,深入浅出,看得真是不亦乐乎。
话不多说,上公式:
这就是大名鼎鼎的贝叶斯公式。
P(A):什么都不知道,发生A的概率。通常称为先验概率。
P(A|X):在已知X发生的前提下,发生A的概率。我们已经有了X的证据了,再来推断A发生的概率,通常称为后验概率。
有什么用呢?
先验和后验,可以说就是贝叶斯的核心所在了。
举个例子吧,通常来讲,一个班级学生的成绩符合正态分布,这个“正态分布”就是先验:我什么数据、样本、证据都没有,我不清楚班上有多少人、不清楚哪怕其中一个人的成绩,得出的事件A。
正态分布有两个参数,平均数u和标准差std,我们知道一个班的成绩符合正态分布,但是是一个怎样的正态分布就不知道了。于是我们需要样本---各个学生的成绩,事件X,在有了X的情况下,我们获得的事件A才有意义。这个明确参数的“正态分布”就是后验:不仅知道它是正态分布,而且知道它是怎样的一个正态分布,得出事件P(A|X),在X的条件下A的情况。
这也符合我们日常的思考逻辑:在信息缺少的情况下,先估摸着得到一个模子,然后不断的从外界获取信息,打磨之前的模子,信息获得的越多越准,模子自然就越精美。
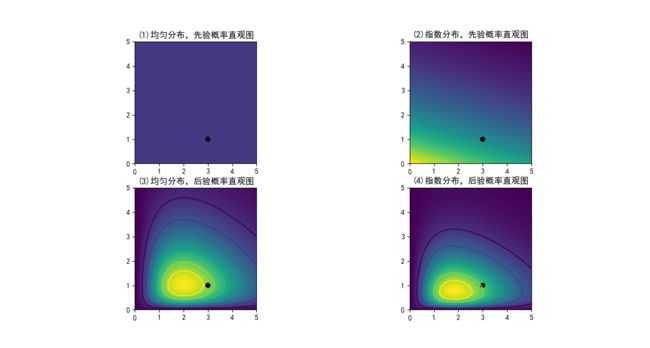
再举个生动点的例子,假如我们现在想对两个参数为lambda1,lambda2的泊松分布进行估计(记住:我们的目的是估计lambda),一开始我们什么都不知道,假设两种情况(两种先验):一、lambda符合均匀分布;二、lambda符合指数分布,下图图一(1)、图一(2)是先验概率的直观图,颜色越深代表概率越大(越有可能发生),显然平均分布在整个空间上每处的概率一致,处处颜色相等,指数分布在靠近0的位置颜色要深些。
上面是先验,搞定了。为弄后验,我们需要样本,就自己生成些样本罢:因为有两个参数lambda1,lambda2,要成两组样本,第一组样本A1由lambda1=1的泊松分布随机生成,第二组样本A2由lambda2=3的泊松分布随机生成。
有了A1,A2两组样本,我们就可以用他们来估计lambda1,lambda2了(事先我们是不知道A1,A2两组样本是符合lambda1=1,lambda2=3的泊松分布的,在这里为了模拟,用它来生成模拟数据A1,A2的)。
从直观图可以看出,当样本数N=1时,对原来的先验空间产生影响,估计值处在真实值lambda1=1,lambda2=3的很大一篇范围内,也就是说,一个样本不足以估计lambda。
N=5,可以看出,估计值在(1,3)这个真实值点的估计范围在缩小。
N=20,50就更小了,这个时候可以估计真实值大概在(1,3)附近
N=100,有了100组样本点,可以说基本就敢断定真实值就在(1,3)了
总结:
先验为均匀分布或指数分布,但参数不可知。可通过一系列的样本,来不断的估计参数值,得到后验。
二、应用篇
import scipy.stats as stats
import numpy as np
from IPython.core.pylabtools import figsize
from matplotlib import pyplot as plt
from matplotlib.pyplot import jet
plt.rcParams['font.sans-serif']=['SimHei']#解约matplotlib画图,中文乱码问题
N=100#样本数
#为产生模拟数据的参数
lambda_1_true = 1
lambda_2_true = 3
#产生poisson分布的两组样本,参数分别是lambda_1_true,lambda_2_true
data = np.concatenate([
stats.poisson.rvs(lambda_1_true,size=(N,1)),
stats.poisson.rvs(lambda_2_true,size=(N,1))
],axis=1)
# print (data)
x = y = np.linspace(.01,5,100)
#pmf:概率质量函数,代表某个点符合poisson的概率大小
likelihood_x =np.array([stats.poisson.pmf(data[:,0],_x)
for _x inx]).prod(axis=1)
likelihood_y =np.array([stats.poisson.pmf(data[:,1],_y)
for _y iny]).prod(axis=1)
L =np.dot(likelihood_x[:,None],likelihood_y[None,:])
# print(likelihood_x)
# print(likelihood_y)
figsize(12.5,12)
#pdf:概率密度函数,在x,y上分别生成两组均匀分布的概率密度
uni_x = stats.uniform.pdf(x,loc=0,scale=5)
uni_y = stats.uniform.pdf(y,loc=0,scale=5)
Mu = np.dot(uni_x[:,None],uni_y[None,:])
#pdf:概率密度函数,在x,y上分别生成两组指数分布的概率密度
exp_x = stats.expon.pdf(x,loc=0,scale=3)
exp_y = stats.expon.pdf(y,loc=0,scale=10)
Me = np.dot(exp_x[:,None],exp_y[None,:])
#第一个图:均分分布
plt.subplot(221)
im = plt.imshow(Mu, interpolation='none',origin='lower', vmax=1, vmin=-.15, extent=(0,5,0,5))
plt.scatter(lambda_2_true,lambda_1_true,c='k',s=50,edgecolors='none')
plt.xlim(0,5)
plt.ylim(0,5)
plt.title('(1)均匀分布,先验概率直观图')
#第二个图:参数为lambda的poisson分布,lambda为均匀分布
plt.subplot(223)
plt.contour(x, y, Mu*L)
im = plt.imshow(Mu*L, interpolation='none',origin='lower', extent=(0,5,0,5))
plt.scatter(lambda_2_true,lambda_1_true,c='k',s=50,edgecolors='none')
plt.xlim(0,5)
plt.ylim(0,5)
plt.title('(3)均匀分布,后验概率直观图')
#第三个图:指数分布
plt.subplot(222)
plt.contour(x, y, Me)
im = plt.imshow(Me, interpolation='none',origin='lower', extent=(0,5,0,5))
plt.scatter(lambda_2_true,lambda_1_true,c='k',s=50,edgecolors='none')
plt.xlim(0,5)
plt.ylim(0,5)
plt.title('(2)指数分布,先验概率直观图')
#第三个图:参数为lambda的poisson分布,lambda为指数分布
plt.subplot(224)
plt.contour(x, y, Me*L)
im = plt.imshow(Me*L, interpolation='none',origin='lower', extent=(0,5,0,5))
plt.scatter(lambda_2_true,lambda_1_true,c='k',s=50,edgecolors='none')
plt.xlim(0,5)
plt.ylim(0,5)
plt.title('(4)指数分布,后验概率直观图')
plt.set_cmap('jet')
plt.show()
参考:《贝叶斯方法-概率编程与贝叶斯推断》