音符起始点检测（音频节奏检测）（7）

原文链接：Onset Detection Part 7: Thresholding & Peak picking

在上一篇文章中，我们看到了如何将一个随着时间的推移而演化为一个简单一维函数的复杂光谱缩减为一个称为光谱通量的函数。在此过程中，我们对频谱通量函数做了一些改进，如校正它和使用汉宁平滑。在这篇文章中，我们将讨论一个所谓的阈值函数，它可以从光谱通量函数推导出来。

（嗯。。。又没有图，尴尬。。。）

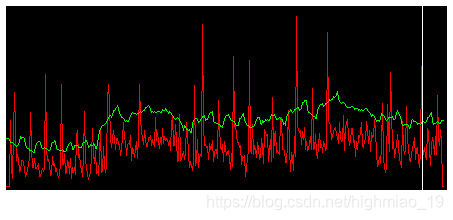
这是一个修正的，汉宁平滑的光谱通量函数。这是 "A Perfect Circle" 中的 "Judith" 这首歌的节选，这张图已经展示了一些峰值，我们可以直接理解为onsets。然而，该函数中仍然存在一些噪声，特别是当 crash 发生时。我们不能再做更好的滤波，比如把函数平滑一点来去掉很多小峰。相反，我们做一些非常简单的事情：我们计算一个阈值函数，它是由光谱通量函数推导出来的。然后，这个阈值函数被用来丢弃噪声频谱通量值。

阈值函数其实很简单。给定我们的光谱通量函数，我们计算每个光谱通量值周围窗口的中值或平均值。假设我们有3000个光谱通量值，每个值都代表1024个样本窗口的光谱通量。44100Hz的采样速率下，1024个样本的时间跨度约为43ms。我们用于阈值函数的窗口大小应该由某个时间值导出，比如我们想要0.5秒时间跨度的平均光谱通量。也就是0.5 / 0.043 = 11个采样窗口或者说11个光谱通量值。对于每个谱通量值，取其前5个样本值，后5个样本值和当前值，计算其平均值。因此，对于每个光谱通量值，我们都得到一个我们称之为阈值的单一值(原因很快就会明了)。下面是一些代码:

public class Threshold 
{
   public static final String FILE = "samples/explosivo.mp3";	
   public static final int THRESHOLD_WINDOW_SIZE = 10;
   public static final float MULTIPLIER = 1.5f;
	
   public static void main( String[] argv ) throws Exception
   {
      MP3Decoder decoder = new MP3Decoder( new FileInputStream( FILE  ) );							
      FFT fft = new FFT( 1024, 44100 );
      fft.window( FFT.HAMMING );
      float[] samples = new float[1024];
      float[] spectrum = new float[1024 / 2 + 1];
      float[] lastSpectrum = new float[1024 / 2 + 1];
      List spectralFlux = new ArrayList( );
      List threshold = new ArrayList( );
	
      while( decoder.readSamples( samples ) > 0 )
      {			
         fft.forward( samples );
         System.arraycopy( spectrum, 0, lastSpectrum, 0, spectrum.length ); 
         System.arraycopy( fft.getSpectrum(), 0, spectrum, 0, spectrum.length );
	
         float flux = 0;
         for( int i = 0; i < spectrum.length; i++ )	
         {
            float value = (spectrum[i] - lastSpectrum[i]);
            flux += value < 0? 0: value;
         }
         spectralFlux.add( flux );					
      }		
		
      for( int i = 0; i < spectralFlux.size(); i++ )
      {
         int start = Math.max( 0, i - THRESHOLD_WINDOW_SIZE );
         int end = Math.min( spectralFlux.size() - 1, i + THRESHOLD_WINDOW_SIZE );
         float mean = 0;
         for( int j = start; j <= end; j++ )
            mean += spectralFlux.get(j);
         mean /= (end - start);
         threshold.add( mean * MULTIPLIER );
      }
		
      Plot plot = new Plot( "Spectral Flux", 1024, 512 );
      plot.plot( spectralFlux, 1, Color.red );		
      plot.plot( threshold, 1, Color.green ) ;
      new PlaybackVisualizer( plot, 1024, new MP3Decoder( new FileInputStream( FILE ) ) );
   }
}

里面没有很多新东西。首先，我们像上一篇文章那样计算光谱通量函数。在此基础上计算了阈值函数。对于ArrayList spectralFlux中的每个谱通量值，我们取其前后的阈值_window_size谱通量值并计算平均值。然后，产生的平均值存储在一个名为threshold的ArrayList中。注意，我们还将每个阈值乘以本例中设置为1.5的乘数。计算完所有的函数后，我们把它们画出来。结果是这样的:

图片来自原文，谁能告诉我怎么去掉水印？

我们刚刚做的是计算光谱通量函数的运行平均值。用这个我们可以检测到所谓的异常值。任何超过阈值函数的值都是异常值，标志着某种类型的开始！还应该清楚为什么阈值函数值乘以常数> 1。异常值必须大于平均值，在本例中是平均值的1.5倍。这个乘法器是一个重要的参数，我们的开始检测器，因为它控制灵敏度。然而，当我将检测器应用于歌曲时，我试图找出一个适用于所有歌曲的单一值。实际上我做到了，并得到了上面使用的神奇的1.5乘法器。它适用于你能在svn中找到的所有样本，以及我测试过的许多其他歌曲。

现在我们把谱通量函数和阈值函数结合起来。基本上我们想要一个修剪后的光谱通量函数，它只包含大于或等于阈值函数的值。我们将上述计划扩展如下:

for( int i = 0; i < threshold.size(); i++ )
{
   if( threshold.get(i) <= spectralFlux.get(i) )
      prunnedSpectralFlux.add( spectralFlux.get(i) - threshold.get(i) );
   else
      prunnedSpectralFlux.add( (float)0 );
}

变量prunnedSpectralFlux只是另一个数组列表。这个循环非常简单，我们在当前光谱通量的prunnedSpectralFlux列表中添加0，使其小于相应的阈值函数值，或者我们添加spectrul flux值减去位置i处的阈值，得到的prunned spectrum flux函数如下:

图片来自原文，谁能告诉我怎么去掉水印？

太棒了，我们快完成了!剩下的就是在这个修剪过的光谱通量中寻找峰值。峰值是一个比下一个值大的值。这就是峰值检测的全部内容。我们快做完了。让我们写一个小代码峰值检测产生一个峰值ArrayList:

for( int i = 0; i < prunnedSpectralFlux.size() - 1; i++ )
{
   if( prunnedSpectralFlux.get(i) > prunnedSpectralFlux.get(i+1) )
      peaks.add( prunnedSpectralFlux.get(i) );
   else
      peaks.add( (float)0 );				
}

就是这样。ArrayList峰值中的任何值> 0现在都是一个开始或跳动。要计算每个峰值中的每个峰值的时间点，只需取其索引并将其乘以原始样本窗口占用的时间跨度。假设我们使用一个采样率为44100Hz的1024个样本窗口，然后我们得到简单的forumula time = index *(1024 / 44100)。就是这样。输出:

图片来自原文，谁能告诉我怎么去掉水印？

做完了。这是我们能写的最基本的起点检测器。让我们回顾一下它的一些性质。与许多系统一样，我们有一些参数可以调整。第一个是样本窗口大小。我几乎总是用1024。降低此值将导致更细粒度的频谱，但可能不会给您带来太多好处。下一个参数是在对样本进行FFT之前对样本进行汉宁平滑。我确实看到了一些改进，但它也会花费你一些周期来计算它。如果您计划在没有FPU的移动设备上实现这一点，那么这一点可能非常重要。每一个节省下来的循环都是一个好的循环。接下来是阈值窗口大小。这可能会对检测阶段的结果产生巨大的影响。我坚持使用一个总共20个散斑通量值的窗口，如上例所示。这是通过计算这20个值所代表的时间跨度来实现的。在一个采样窗口中1024个采样频率为44100Hz的样本大约有一秒钟的数据。该值在我测试的所有类型的简单检测器上都运行得很好，但您的会可能有所不同。最后一个可能也是最重要的参数是阈值函数的乘数。低时探测器是敏感的，高时什么都得不到。在我的日常工作中，我有时不得不做异常值分析，这和我们在这里做的很相似。有时我使用简单的基于阈值的方法，当基于统计的离群点检测相对于某些方法时，1.3-1.6之间的值似乎是某种神奇的数字。我认为阈值乘法器和阈值窗口大小应该是惟一需要调整的参数。忘记其他的，使用缺省值1024作为样本窗口大小和汉宁平滑。将一个参数分解为多个参数并不有趣，因此在这种情况下，将其简化为“只有”两个参数是有意义的。我在上面给出的默认值与我们在本系列中开发的检测器配合得相当好。如果你做多波段分析，你可能不得不为每个波段分别调整它们。

剩下的是一些改进，比如这个完整的过程不是针对整个频谱而是针对子波段，这样我们就可以对各种乐器进行起点检测(就像我们所知道的，这些乐器在频率范围内重叠)。另一个改进是使用重叠的样本窗口，比如50%。这使傅里叶变换平滑了一点，得到了更好的结果。我们也可以尝试对整个音频信号进行动态范围压缩然后再将其传递给FFT等等。框架中的代码允许您轻松地试验各种附加步骤。您还可能需要清理产生的峰值列表，并删除任何接近的峰值，比如< 10ms。“边做边学”是最大的箴言。现在出去写一些很棒的音乐游戏吧！我在处理这个工作的过程中发现了几个非常有用的论文和链接:

http://www.dspguide.com/ 一个不错的在线图书(也可用精装)称为“科学家和工程师的指导数字信号处理”以任何你想了解数字信号处理(作为一个工程师:))。

https://ccrma.stanford.edu/~jos/dft/ 另一本在线书籍名为《音频应用的离散傅里叶变换数学》，处理任何与离散傅里叶变换相关的问题。数学很重，但阅读很好。

http://old.lam.jussieu.fr/src/Membres/Daudet/Publications_files/Onset_Tutorial.pdf 这是一篇非常好的科学论文，名为“音乐信号起始检测教程”。特点是具有不同的起效检测功能(这里我们使用的是非带状光谱通量)，以及一些关于标准化数据集上各种功能性能的数据(Mirex 2006起效检测挑战)。看看贝罗的其他文章，他似乎是这个领域的重要人物。

http://www.dafx.ca/proceedings/papers/p_133.pdf Dixon是该领域的另一位知名人士(至少从引文数量来看是这样，但我们都知道它们真正告诉了你多少……)。很好的论文，一定要读。

如果你查看一下谷歌schoolar上提到的两篇论文的引文图，你会发现更多关于起点检测的论文，它们可能会引起你的兴趣。在这种情况下，谷歌是您的朋友。总能读到好论文!