糖尿病预测项目
这次我们要学习的项目是糖尿病的预测,数据保存在diabetes.csv文件中。数据一共有8个特征和1个标签:
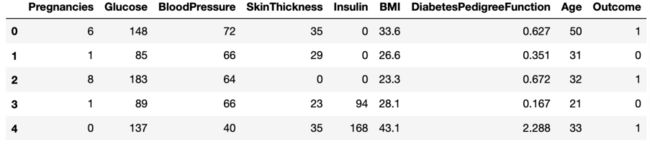
Pregnancies:怀孕次数Glucose:葡萄糖测试值BloodPressure:血压SkinThickness:皮肤厚度Insulin:胰岛素BMI:身体质量指数DiabetesPedigreeFunction:糖尿病遗传函数Age:年龄Outcome:糖尿病标签,1表示有糖尿病,0表示没有糖尿病
首先先载入一些常用模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
然后用pandas读入数据
diabetes_data = pd.read_csv('diabetes.csv')
diabetes_data.head()
# 查看数据信息
diabetes_data.info(verbose=True)
RangeIndex: 768 entries, 0 to 767
Data columns (total 9 columns):
Pregnancies 768 non-null int64
Glucose 768 non-null int64
BloodPressure 768 non-null int64
SkinThickness 768 non-null int64
Insulin 768 non-null int64
BMI 768 non-null float64
DiabetesPedigreeFunction 768 non-null float64
Age 768 non-null int64
Outcome 768 non-null int64
dtypes: float64(2), int64(7)
memory usage: 54.1 KB
我们从上面可以看到一共有768个数据,并且所有的特征和标签都是768个值,所有没有缺失数据。并且所有数据都是数值类型(int64 or float64)的数据。
# 数据描述
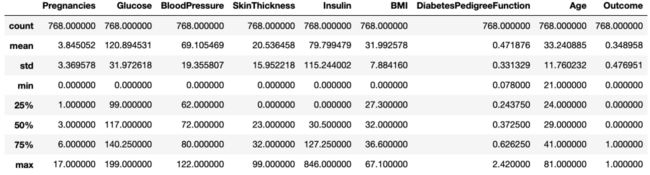
diabetes_data.describe()
通过describe我们可以观察到数据的数量,平均值,标准差,最小值,最大值等数据。
# 数据形状
diabetes_data.shape
(768, 9)
# 查看标签分布
print(diabetes_data.Outcome.value_counts())
# 使用柱状图的方式画出标签个数统计
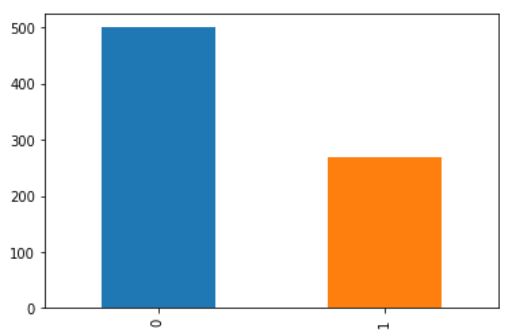
p=diabetes_data.Outcome.value_counts().plot(kind="bar")
0 500
1 268
Name: Outcome, dtype: int64
# 可视化数据分布
p=sns.pairplot(diabetes_data, hue = 'Outcome')
图片可能需要放大才能看清楚。这里画的图主要是两种类型,直方图和散点图。单一特征对比的时候用的是直方图,不同特征对比的时候用的是散点图,显示两个特征的之间的关系。观察数据分布我们可以发现一些异常值,比如Glucose葡萄糖,BloodPressure血压,SkinThickness皮肤厚度,Insulin胰岛素,BMI身体质量指数这些特征应该是不可能出现0值的。但是数据分布中却有很多0值。
# 把葡萄糖,血压,皮肤厚度,胰岛素,身体质量指数中的0替换为nan
colume = ['Glucose', 'BloodPressure', 'SkinThickness', 'Insulin', 'BMI']
diabetes_data[colume] = diabetes_data[colume].replace(0,np.nan)
# 查看数据空值情况
import missingno as msno
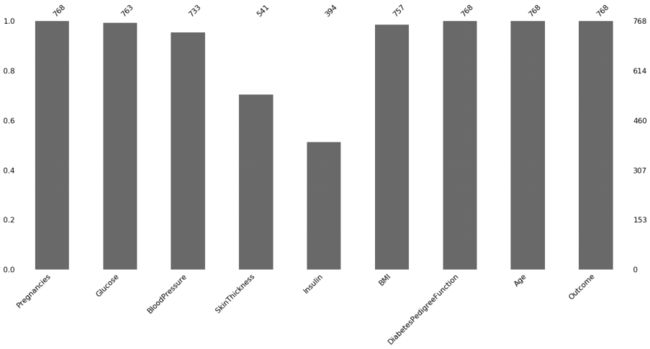
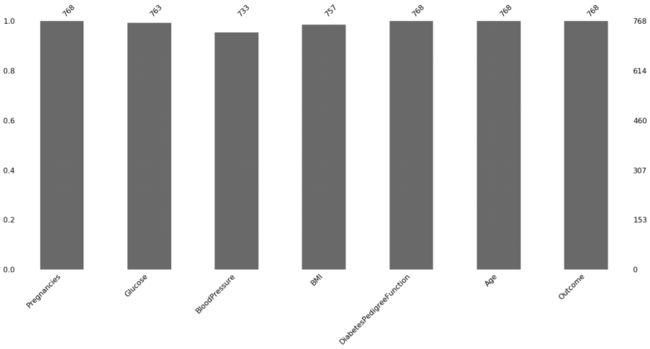
p=msno.bar(diabetes_data)
图中可以看到葡萄糖,血压,皮肤厚度,胰岛素,身体质量指数都是存在空值的,并且皮肤厚度和胰岛素中的空值特别多。
# 设定阀值
thresh_count = diabetes_data.shape[0]*0.8
# 若某一列数据缺失的数量超过20%就会被删除
diabetes_data = diabetes_data.dropna(thresh=thresh_count, axis=1)
p=msno.bar(diabetes_data)
把空值超过20%的特征都去除掉之后,只剩下6个特征。
# 导入插补库
from sklearn.preprocessing import Imputer
# 对数值型变量的缺失值,我们采用均值插补的方法来填充缺失值
imr = Imputer(missing_values='NaN', strategy='mean', axis=0)
colume = ['Glucose', 'BloodPressure', 'BMI']
# 进行插补
diabetes_data[colume] = imr.fit_transform(diabetes_data[colume])
p=msno.bar(diabetes_data)
使用特征的平均值给特征中的缺失值进行填充,填充后所有的数据就没有空值了。
plt.figure(figsize=(12,10))
# 画热力图,数值为两个变量之间的相关系数
p=sns.heatmap(diabetes_data.corr(), annot=True)
热力图可能也需要放大来看,它是表示两个数据之间的相关性,数值范围是-1到1之间,大于0表示两个数据是正相关的,小于0表示两个数据是负相关的,等于0就是不相关。我们可以看到有一条对角线上的数值都是1,两个数据如果是相同的两个数据,那么他们的相关系数就是1。并且这个相关系数矩阵是对称的。
我们可以观察到一些比较明显的特征,比如Age年龄跟Pregnancies怀孕次数有比较强的相关性,也就是说年龄越大怀孕次数就越多,或者怀孕次数越多年龄就越大,这应该是比较合理的一个情况。
糖尿病的标签Outcome和Glucose葡萄糖测试值正相关系数比较大,也就是说葡萄糖测试值比较高的话,那么就很可能患有糖尿病。
# 把数据切分为特征x和标签y
x = diabetes_data.drop("Outcome",axis = 1)
y = diabetes_data.Outcome from sklearn.model_selection import train_test_split
# 切分数据集,test_size=0.3表示30%为测试集。stratify=y表示切分后训练集和测试集中的数据类型的比例跟切分前y中的比例一致
# 比如切分前y中0和1的比例为1:2,切分后y_train和y_test中0和1的比例也都是1:2
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.3, stratify=y)
# 导入KNN算法
from sklearn.neighbors import KNeighborsClassifier
# 保存不同k值测试集准确率
test_scores = []
# 保存不同k值训练集准确率
train_scores = []
x_train_values = x_train.values
y_train_values = y_train.values
# 设置30个k值
k = 30
for i in range(1,k):
knn = KNeighborsClassifier(i)
knn.fit(x_train,y_train)
# 保存测试集准确率
test_scores.append(knn.score(x_test,y_test))
# 保存训练集准确率
train_scores.append(knn.score(x_train,y_train))
plt.title('k-NN Varying number of neighbors')
plt.plot(range(1,k),test_scores,label="Test")
plt.plot(range(1,k),train_scores,label="Train")
plt.legend()
plt.xticks(range(1,k))
plt.xlabel('k')
plt.ylabel('accuracy')
plt.show()
不同k值得到不同的准确率结果。
# 选择一个最好的k值作为模型参数
k = np.argmax(test_scores)+1
knn = KNeighborsClassifier(k)
knn.fit(x_train,y_train)
knn.score(x_test,y_test)
0.8138528138528138
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
y_pred = knn.predict(x_test)
print(classification_report(y_pred, y_test))
precision recall f1-score support
0 0.88 0.84 0.86 157
1 0.69 0.76 0.72 74
micro avg 0.81 0.81 0.81 231
macro avg 0.79 0.80 0.79 231
weighted avg 0.82 0.81 0.82 231
macro avg:宏平均,所有类的算数平均数micro avg:分母就是输入分类器的预测样本个数,分子就是预测正确的样本个数weighted avg:加权平均,每个类别的权值为:类别suppot/总suppot
confusion = confusion_matrix(y_pred, y_test)
df_cm = pd.DataFrame(confusion)
sns.heatmap(df_cm, annot=True)
混淆矩阵,测试集中非糖尿病被预测为非糖尿病有130例,糖尿病被预测为糖尿病有56例,非糖尿病被预测为糖尿病有25例,糖尿病被预测为非糖尿病有18例子。