图之邻接表详解（C语言版）

---

一、定义

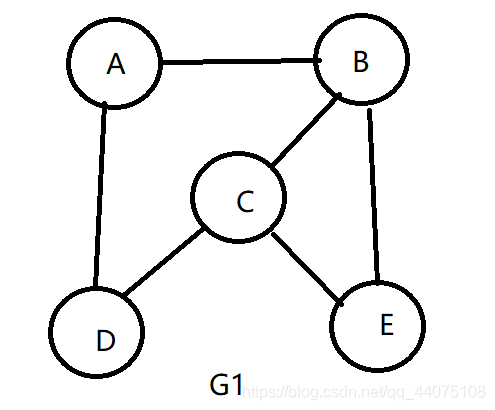
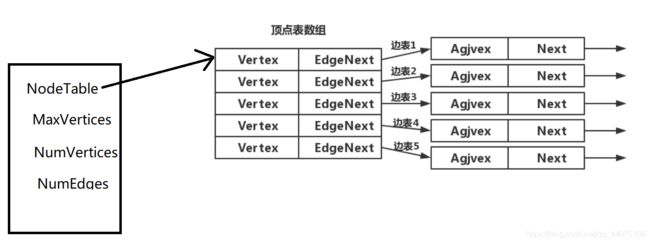
        图的邻接表是一种顺序与链式存储相结合的存储方式。下面给出一个示例，以便大家能够理解邻接表这种存储方式：
        无向图G1

        用邻接表来存储G1

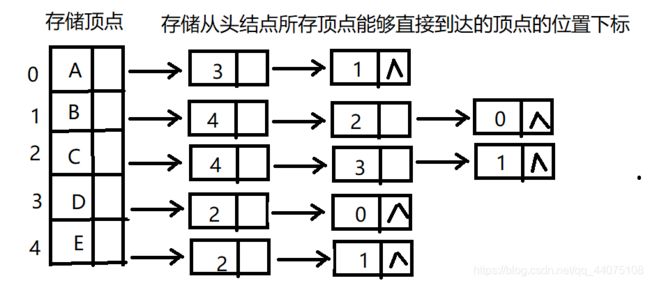
        每一个顶点所在结点都是之后链表的头结点，之后的链表结点存放从头结点所存顶点能够直接到达顶点的位置下标，如顶点A能够直接到达D，B两个顶点，D的顶点存放在3位置，B顶点存放在1位置，所以A之后的链表结点存放的值为3和1

二、结构

        结构图

        代码描述

//顶点默认元素个数
#define Default_Vertex_Size 10
#define T  char //顶点元素类型
//边结构
typedef struct Edge
{
     
	int dest;  //存放顶点下标
	struct Edge *link;//连接下一个顶点
}Edge;
//顶点结构
typedef struct Vertex
{
     
	T data;//顶点数据
	Edge *adj;//指向边结构指针
}Vertex;
//邻接表
typedef struct GraphLnk
{
     
	int MaxVertices; //最大顶点个数
	int NumVertices; //实际顶点个数
	int NumEdges;  //边的条数

	Vertex *NodeTable; //指向顶点结构表
}GraphLnk;

三、常用操作

        下面给出存储无向图的邻接表的常用操作（有向图类似）

        初始化

//初始化
void InitGraph(GraphLnk *g)
{
     
	g->MaxVertices = Default_Vertex_Size;//初始化最大顶点个数
	g->NumEdges = g->NumVertices = 0;//初始化实际顶点个数和边条数
	//为顶点结构表开辟空间
	g->NodeTable = (Vertex*)malloc(sizeof(Vertex) * g->MaxVertices);
	assert(g->NodeTable != NULL);
	for(int i=0; i<g->MaxVertices; ++i)//顶点结构表的初始化
	{
     
		g->NodeTable[i].adj = NULL;
	}
}

        获取顶点位置

//获取顶点位置
int  GetVertexPos(GraphLnk *g, T v)
{
     
	for(int i=0; i<g->NumVertices; ++i)
	{
     
		if(g->NodeTable[i].data == v)//判断是否找到
			return i;
	}
	return -1;
}

        打印图

//打印图
void ShowGraph(GraphLnk *g)
{
     
	Edge *p;
	for(int i=0; i<g->NumVertices; ++i)//对顶点进行遍历
	{
     
		printf("%d %c:>",i,g->NodeTable[i].data);//输出顶点
		p = g->NodeTable[i].adj;//指向边结构
		while(p != NULL)//打印相连的顶点
		{
     
			printf("%d-->",p->dest);
			p = p->link;
		}
		printf("Nul.\n");
	}
	printf("\n");
}

插入顶点

//插入顶点
void InsertVertex(GraphLnk *g, T v)
{
     
	//判断顶点表是否已满
	if(g->NumVertices >= g->MaxVertices)
		return;
	g->NodeTable[g->NumVertices++].data = v;//插入
}

        插入边

//插入边：在顶点vertex1和vertex2之间插入一条边
void InsertEdge(GraphLnk *g, T vertex1, T vertex2)
{
     
	int v1 = GetVertexPos(g,vertex1);//获取vertex1的位置
	int v2 = GetVertexPos(g,vertex2);//获取vertex2的位置
	if(v1==-1 || v2==-1)
		return;

	Edge *s;
	//无向图是双向的插入要两次
	//插入V1 --> V2的边 头插法插入
	s = (Edge *)malloc(sizeof(Edge));
	assert(s != NULL);
	s->dest = v2;
	s->link = g->NodeTable[v1].adj;
	g->NodeTable[v1].adj = s;

	//插入V2 --> V1的边 头插法插入
	s = (Edge *)malloc(sizeof(Edge));
	assert(s != NULL);
	s->dest = v1;
	s->link = g->NodeTable[v2].adj;
	g->NodeTable[v2].adj = s;

	g->NumEdges++;
}

        删除边

//删除一条边：删除顶点vertex1和顶点vertex2之间的边
void RemoveEdge(GraphLnk *g, T vertex1, T vertex2)
{
     
	int v1 = GetVertexPos(g,vertex1);//获取v1所在位置
	int v2 = GetVertexPos(g,vertex2);//获取顶点v2所在位置

	if(v1==-1 || v2==-1)
		return;

	Edge *q = NULL;
	Edge *p;
	//无向图是双向的，所以需要删除两边相对的边
	//删除v1 -- > v2的边
	p = g->NodeTable[v1].adj;
	while(p != NULL && p->dest != v2)
	{
     //从v1后面的链表中查找v2顶点，其中q指向v2顶点的前驱,p指向v2顶点
		q = p;
		p = p->link;
	}
	if(p == NULL)
		return;

	if(q == NULL)//判断找到的结点是否是链表内的第一个结点
	{
     //是  头删
		g->NodeTable[v1].adj = p->link;//头删
	}
	else
	{
     //不是 直接删除
		q->link = p->link;
	}
	free(p); //释放空间

	//删除v2 --> v1的边
	q = NULL;
	p = g->NodeTable[v2].adj;
	while(p->dest != v1)
	{
     //从v2后面的链表中查找v1顶点，其中q指向v1顶点的前驱,p指向v1顶点
		q = p;
		p = p->link;
	}
	if(q==NULL)//判断找到的结点是否是链表内的第一个结点
	{
     //是  头删
		g->NodeTable[v2].adj = p->link;
	}
	else
	{
     //不是 直接删除
		q->link = p->link;
	}
	free(p); //释放空间
	g->NumEdges--; //边数减一
}

        删除顶点

//删除顶点
void RemoveVertex(GraphLnk *g, T vertex)
{
     
	int v = GetVertexPos(g,vertex);//获取顶点vertex的位置
	if(v == -1)
		return;

	//删除顶点所相连的边
	Edge *p = g->NodeTable[v].adj;//获取与顶点vertex相连的链表

	int k;
	Edge *t = NULL;//t是s的前驱
	Edge *s;
	while(p!=NULL)
	{
     
		k = p->dest;//获取与v相连的顶点k
		s = g->NodeTable[k].adj;//获取与k连接的链表
		while(s!=NULL && s->dest!=v)//从该链表中查找与v连接的结点
		{
     
			t = s;
			s = s->link;
		}
		if(s!=NULL)//判断是否找到
		{
     //找到
			if(t==NULL)//判断是否是第一个结点
			{
     //是  头删
				g->NodeTable[k].adj = s->link;
			}
			else
			{
     //否 直接删除
				t->link = s->link;
			}
			free(s);//释放空间
		}
		//释放与v连接链表中的k结点
		g->NodeTable[v].adj = p->link;
		free(p);
		p = g->NodeTable[v].adj;
	}
	
	g->NumVertices--;//顶点数减一
	//拿最后一个顶点的值覆盖要删除的顶点
	g->NodeTable[v].data = g->NodeTable[g->NumVertices].data;
	g->NodeTable[v].adj = g->NodeTable[g->NumVertices].adj;

	//调整链表内结点的指向：将原来标明到最后一个顶点的结点，标明到最后一个结点更改后的位置
	s = g->NodeTable[v].adj;//指向原来与最后一个顶点连接的链表
	while(s != NULL)//对链表进行搜索，看哪些顶点与原来最后一个顶点相连
	{
     
		k = s->dest;//获取相连的顶点位置
		p = g->NodeTable[k].adj;//找到与相邻顶点连接的链表
		while(p != NULL)//对该链表进行搜索
		{
     
			if(p->dest == g->NumVertices)//判断是否找到指向最后一个顶点的结点
			{
     //找到
				p->dest = v;//更换指向，指向最后一个顶点更新后的位置
				break;
			}
			p = p->link;//没找到，则继续查找下一个
		}
		s = s->link;//进入下一个结点，准备下一个顶点链表结点的替换
	}
}

        获取第一个邻接顶点

//获取第一个邻接顶点
int  GetFirstNeighbor(GraphLnk *g, T vertex)
{
     
	int v = GetVertexPos(g,vertex);//获取顶点vertex的位置
	if(v == -1)
		return -1;
	//从vertex所连接链表的第一个结点处取得第一个邻接顶点
	Edge *p = g->NodeTable[v].adj;
	if(p != NULL)
		return p->dest;
	return -1;
}

        获取邻接顶点的下一个顶点

//获取邻接顶点的下一个顶点：获取顶点vertex1的邻接顶点，该邻接顶点在vertex1的邻接顶点vertex2的下一个
int  GetNextNeighbor(GraphLnk *g,  T vertex1, T vertex2)
{
     
	int v1 = GetVertexPos(g,vertex1);//获取vertex1的位置
	int v2 = GetVertexPos(g,vertex2);//获取vertex2的位置
	if(v1==-1 || v2==-1)
		return -1;

	Edge *p = g->NodeTable[v1].adj;//获取与顶点vertex1相连的链表
	while(p != NULL && p->dest != v2)//从链表中查找到指向vertex2顶点的结点位置
		p = p->link;
	if(p!=NULL && p->link!=NULL)//判断是否找到
		return p->link->dest;//找到，那么它的下一个结点就是所求的邻接顶点
	return -1;
}

        销毁图

//销毁图
void DestroyGraph(GraphLnk *g)
{
     
	Edge *p;
	//释放每一个顶点指向的链表空间
	for(int i=0; i<g->NumVertices; ++i)
	{
     
		p = g->NodeTable[i].adj;
		while(p != NULL)
		{
     
			g->NodeTable[i].adj = p->link;
			free(p);
			p = g->NodeTable[i].adj;
		}
	}
	//释放存放顶点的空间
	free(g->NodeTable);
	g->NodeTable = NULL;
	g->MaxVertices = g->NumEdges = g->NumVertices = 0;
}

结语

        对图的邻接表的介绍就到这里啦，希望这篇文章能给予你一些帮助，感谢各位人才的：点赞、收藏和评论，我们下次见。

附录

        测试代码：图之邻接表详解（C语言版）