Python计算余弦相似度及向量范数
目录
1、Python求余弦相似度
计算两个句子向量
2、np.linalg.norm 求 向量模长(一范二范)
3、python列表转换为矩阵
1、Python求余弦相似度
在非直角三角形中,余弦定理的公式是:
![]()
![]()
在向量表示的三角形中,假设a向量是(x1, y1),b向量是(x2, y2),那么可以将余弦定理改写成下面的形式:
![]()
![]()
扩展,如果向量a和b不是二维而是n维,上述余弦的计算法仍然正确。假定a和b是两个n维向量,则a与b的夹角 的余弦等于:
![]()
计算两个句子向量
句子A:(1,1,2,1,1,1,0,0,0)
和句子B:(1,1,1,0,1,1,1,1,1)的向量余弦值来确定两个句子的相似度。
根据:
![]()
计算过程及(通用)代码如下:
![]()
1、调用sklearn
from sklearn.metrics.pairwise import cosine_similarity
a = [[1, 3, 2], [2, 2, 1]]
print(cosine_similarity(a))2、方法1,常规算法,计算较慢
def cos_sim(s1_cut_code, s2_cut_code):
# 计算余弦相似度
sum = 0
sq1 = 0
sq2 = 0
for i in range(len(s1_cut_code)):
sum += s1_cut_code[i] * s2_cut_code[i]
sq1 += pow(s1_cut_code[i], 2)
sq2 += pow(s2_cut_code[i], 2)
try:
result = round(float(sum) / (math.sqrt(sq1) * math.sqrt(sq2)), 3)
except ZeroDivisionError:
result = 0.0
# print("余弦相似度为:%f"%result)
return result方法2 计算较快
def norm(vector):
return math.sqrt(sum(x * x for x in vector))
def cosine_similarity(vec_a, vec_b):
norm_a = norm(vec_a)
norm_b = norm(vec_b)
dot = sum(a * b for a, b in zip(vec_a, vec_b))
return dot / (norm_a * norm_b)3、稀疏矩阵
def computer_simMatrix(c):
"""
稀疏矩阵求相似度矩阵
"""
return c.dot(c.T)/sparse.linalg.norm(c,axis=1).reshape((-1,1)).dot(sparse.linalg.norm(c,axis=1).reshape((1,-1)))
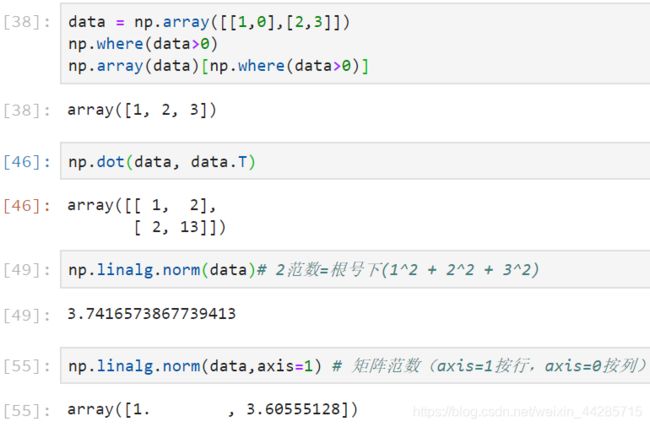
2、np.linalg.norm 求 向量模长(一范二范)
x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False)
①x: 表示矩阵(也可以是一维)
②ord:范数类型
向量的范数:
![]()
矩阵的范数:
ord=1:列和的最大值
ord=2:|λE-ATA|=0,求特征值,然后求最大特征值得算术平方根
ord=∞:行和的最大值
③axis:处理类型
axis=1表示按行向量处理,求多个行向量的范数
axis=0表示按列向量处理,求多个列向量的范数
axis=None表示矩阵范数。
④keepding:是否保持矩阵的二维特性
True表示保持矩阵的二维特性,False相反
A = np.array([[3,4],[-6,5]])
ret = np.linalg.norm(A,ord=None) # 对象是矩阵,求矩阵元素平方和开放
print(ret)
ret = np.linalg.norm(A,ord=None,axis=1) # 对象是逐行,求每行元素平方和开放
print(ret)
ret = np.linalg.norm(A,ord=None,axis=0) # 对象是逐列,求每列元素平方和开放
print(ret)# 对象是矩阵,求矩阵中逐行元素绝对值和的最大值
ret = np.linalg.norm(A,ord=np.Inf)
print(ret)
ret = np.linalg.norm(A,ord=np.Inf,axis=1) # 对象是逐行,求每行元素绝对值和的最大值
print(ret)
ret = np.linalg.norm(A,ord=np.Inf,axis=0) # 对象是逐列,求每列元素绝对值的最大值
print(ret)
# 对象是矩阵,求矩阵中逐行元素绝对值和的最小值
ret = np.linalg.norm(A,ord=-np.Inf)
print(ret)
ret = np.linalg.norm(A,ord=-np.Inf,axis=1) # 对象是逐行,求行的元素绝对值的最小值
print(ret)
ret = np.linalg.norm(A,ord=-np.Inf,axis=0) # 对象是逐列,求列的元素绝对值的最小值
print(ret)A = np.array([[3,-4,1],[-6,5,0]])
ret = np.linalg.norm(A,ord=0,axis=1) # 对象是逐行,求每行的非零元素个数
print(ret)
ret = np.linalg.norm(A,ord=0,axis=0) # 对象是逐列,求每列的非零元素个数
print(ret)A = np.array([[100,4],[-6,5]])
ret = np.linalg.norm(A,ord=1) # 对象是矩阵,求列的元素绝对值和的最大值
print(ret)
ret = np.linalg.norm(A,ord=1,axis=1) # 对象是逐行,求行的元素绝对值和
print(ret)
ret = np.linalg.norm(A,ord=1,axis=0) # 对象是逐列,求;列的元素绝对值和
print(ret)A = np.array([[-4,3,1],[-6,5,-1]])
ret = np.linalg.norm(A,ord=-1) # 对象是矩阵,求列的元素绝对值和最小值
print(ret)
ret = np.linalg.norm(A,ord=-1,axis=1) # 对象是逐行
print(ret)
ret = np.linalg.norm(A,ord=-1,axis=0) # 对象是逐列
print(ret)A = np.array([[-4, 3, 4],
[-6, 4, 3]])
#10.0015300174, 对象是矩阵,求所有元素平方和开方,所有元素平方和102,开方=10.0015300174
ret = np.linalg.norm(A, ord=2)
#[ 6.40312424 7.81024968],对象是每行,求行的元素平方和开方
ret = np.linalg.norm(A, ord=2, axis=1)
#[ 7.21110255 5. 5.],对象是每列,求列的元素平方和开方
ret = np.linalg.norm(A, ord=2, axis=0)3、python列表转换为矩阵
#创建列表
>>> l=[] //然后用列表的insert函数将系数项插入到列表中去,最后将列表转换为矩阵
insert(“插入位置”,插入的内容对象)
>>> l.insert(0,[9,52,381])
>>> l
[[9, 52, 381]]
>>> l.insert(1,[52,381,3017])
>>> l
[[9, 52, 381], [52, 381, 3017]]
>>> l.insert(2,[381,3017,25317])
>>> l
[[9, 52, 381], [52, 381, 3017], [381, 3017, 25317]]
>>> a=np.mat(l)#这里将列表转换为矩阵
>>> a
matrix([[ 9, 52, 381],
[ 52, 381, 3017],
[ 381, 3017, 25317]])
>>> l=[]
>>> l.insert(0,[32])
>>> l.insert(1,[147])
>>> l.insert(2,[1025])
>>> l
[[32], [147], [1025]]
>>> b=np.mat(l)#将列表转换为矩阵
>>> b
matrix([[ 32],
[ 147],
[1025]])
scipy.sparse的一些整理 https://blog.csdn.net/qq_33466771/article/details/80304498
Scipy教程 - 线性代数库scipy.linalg http://blog.csdn.net/pipisorry/article/details/43277755
相似度算法之余弦相似度 https://blog.csdn.net/zz_dd_yy/article/details/51926305
python求向量的三种范式 https://blog.csdn.net/wangdong2017/article/details/81297654