1 背景
主成分分析法是数据挖掘中常用的一种降维算法,是Pearson在1901年提出的,再后来由hotelling在1933年加以发展提出的一种多变量的统计方法,其最主要的用途在于“降维”,通过析取主成分显出的最大的个别差异,也可以用来削减回归分析和聚类分析中变量的数目,与因子分析类似。
所谓降维,就是把具有相关性的变量数目减少,用较少的变量来取代原先变量。如果原始变量互相正交,即没有相关性,则主成分分析没有效果。
在生物信息学的实际应用情况中,通常是得到了成百上千个基因的信息,这些基因相互之间会有影响,通过主成分分析后,得到有限的几个主成分就可以代表它们的基因了。也就是所谓的降维。
R语言有非常多的途径做主成分分析,比如自带的princomp()和psych包的principal()函数,还有gmodels包的fast.prcomp函数。
2 拆解主成分分析步骤
实际应用时我们通常会选择主成分分析函数,直接把input数据一步分析到位,只需要看懂输出结果即可。但是为了加深理解,这里一步步拆解主成分分析步骤,讲解原理。
2.1 测试数据
数据集USJudgeRatings包含了律师对美国高等法院法官的评分。数据框包含43个样本,12个变量!
下面简单看一看这12个变量是什么,以及它们的相关性。
library(knitr)
kable(head(USJudgeRatings))
| CONT | INTG | DMNR | DILG | CFMG | DECI | PREP | FAMI | ORAL | WRIT | PHYS | RTEN | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AARONSON,L.H. | 5.7 | 7.9 | 7.7 | 7.3 | 7.1 | 7.4 | 7.1 | 7.1 | 7.1 | 7.0 | 8.3 | 7.8 |
| ALEXANDER,J.M. | 6.8 | 8.9 | 8.8 | 8.5 | 7.8 | 8.1 | 8.0 | 8.0 | 7.8 | 7.9 | 8.5 | 8.7 |
| ARMENTANO,A.J. | 7.2 | 8.1 | 7.8 | 7.8 | 7.5 | 7.6 | 7.5 | 7.5 | 7.3 | 7.4 | 7.9 | 7.8 |
| BERDON,R.I. | 6.8 | 8.8 | 8.5 | 8.8 | 8.3 | 8.5 | 8.7 | 8.7 | 8.4 | 8.5 | 8.8 | 8.7 |
| BRACKEN,J.J. | 7.3 | 6.4 | 4.3 | 6.5 | 6.0 | 6.2 | 5.7 | 5.7 | 5.1 | 5.3 | 5.5 | 4.8 |
| BURNS,E.B. | 6.2 | 8.8 | 8.7 | 8.5 | 7.9 | 8.0 | 8.1 | 8.0 | 8.0 | 8.0 | 8.6 | 8.6 |
这12个变量的介绍如下:
[,1] CONT Number of contacts of lawyer with judge.
[,2] INTG Judicial integrity.司法诚实性
[,3] DMNR Demeanor.风度;举止;行为
[,4] DILG Diligence.勤奋,勤勉;注意的程度
[,5] CFMG Case flow managing.
[,6] DECI Prompt decisions.
[,7] PREP Preparation for trial.
[,8] FAMI Familiarity with law.
[,9] ORAL Sound oral rulings.
[,10] WRIT Sound written rulings.
[,11] PHYS Physical ability.
[,12] RTEN Worthy of retention.
这些是专业领域的用词,大家可以先不用纠结具体细节。
2.2 为什么要做主成分分析
不管三七二十一就直接套用统计方法都是耍流氓,做主成分分析并不是拍脑袋决定的。 在这个例子里面,我们拿到了这43个法官的12个信息,就可以通过这12个指标来对法官进行分类,但也许实际情况下收集其他法官的12个信息比较麻烦,所以我们希望只收集三五个信息即可,然后也想达到比较好的分类效果。或者至少也得剔除几个指标吧,这个时候主成分分析就能派上用场啦。这12个变量能得到12个主成分,如果前两个主成分可以揭示85%以上的变异度,也就是说我们可以用两个主成分来代替那12个指标。
在生物信息学领域,比如我们测了1000个病人的2万个基因的表达矩阵,同时也有他们的健康状态信息。那么我们想仔细研究这些数据,想得到基因表达与健康状态的某种关系。这样我就可以对其余几十亿的人检测基因表达来预测其健康状态。如果我们进行了主成分分析,就可以选择解释度比较高的主成分对应的基因,可能就几十上百个而已,大幅度的降低广泛的基因检测成本。
2.3 step1:数据标准化(中心化)
dat_scale=scale(USJudgeRatings,scale=F)
options(digits=4, scipen=4)
kable(head(dat_scale))
| CONT | INTG | DMNR | DILG | CFMG | DECI | PREP | FAMI | ORAL | WRIT | PHYS | RTEN | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AARONSON,L.H. | -1.7372 | -0.1209 | 0.1837 | -0.393 | -0.3791 | -0.1651 | -0.3674 | -0.3884 | -0.193 | -0.3837 | 0.3651 | 0.1977 |
| ALEXANDER,J.M. | -0.6372 | 0.8791 | 1.2837 | 0.807 | 0.3209 | 0.5349 | 0.5326 | 0.5116 | 0.507 | 0.5163 | 0.5651 | 1.0977 |
| ARMENTANO,A.J. | -0.2372 | 0.0791 | 0.2837 | 0.107 | 0.0209 | 0.0349 | 0.0326 | 0.0116 | 0.007 | 0.0163 | -0.0349 | 0.1977 |
| BERDON,R.I. | -0.6372 | 0.7791 | 0.9837 | 1.107 | 0.8209 | 0.9349 | 1.2326 | 1.2116 | 1.107 | 1.1163 | 0.8651 | 1.0977 |
| BRACKEN,J.J. | -0.1372 | -1.6209 | -3.2163 | -1.193 | -1.4791 | -1.3651 | -1.7674 | -1.7884 | -2.193 | -2.0837 | -2.4349 | -2.8023 |
| BURNS,E.B. | -1.2372 | 0.7791 | 1.1837 | 0.807 | 0.4209 | 0.4349 | 0.6326 | 0.5116 | 0.707 | 0.6163 | 0.6651 | 0.9977 |
scale()是对数据中心化的函数,当参数scale=F时,表示将数据按列减去平均值,scale=T表示按列进行标准化,公式为(x-mean(x))/sd(x),本例采用中心化。
2.4 step2:求相关系数矩阵
dat_cor=cor(dat_scale)
options(digits=4, scipen=4)
kable(dat_cor)
| CONT | INTG | DMNR | DILG | CFMG | DECI | PREP | FAMI | ORAL | WRIT | PHYS | RTEN | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CONT | 1.0000 | -0.1332 | -0.1537 | 0.0124 | 0.1369 | 0.0865 | 0.0115 | -0.0256 | -0.0120 | -0.0438 | 0.0542 | -0.0336 |
| INTG | -0.1332 | 1.0000 | 0.9646 | 0.8715 | 0.8141 | 0.8028 | 0.8778 | 0.8689 | 0.9114 | 0.9088 | 0.7419 | 0.9373 |
| DMNR | -0.1537 | 0.9646 | 1.0000 | 0.8369 | 0.8134 | 0.8041 | 0.8558 | 0.8412 | 0.9068 | 0.8931 | 0.7887 | 0.9437 |
| DILG | 0.0124 | 0.8715 | 0.8369 | 1.0000 | 0.9588 | 0.9562 | 0.9786 | 0.9574 | 0.9545 | 0.9593 | 0.8129 | 0.9300 |
| CFMG | 0.1369 | 0.8141 | 0.8134 | 0.9588 | 1.0000 | 0.9811 | 0.9579 | 0.9355 | 0.9506 | 0.9422 | 0.8795 | 0.9271 |
| DECI | 0.0865 | 0.8028 | 0.8041 | 0.9562 | 0.9811 | 1.0000 | 0.9571 | 0.9428 | 0.9483 | 0.9461 | 0.8718 | 0.9250 |
| PREP | 0.0115 | 0.8778 | 0.8558 | 0.9786 | 0.9579 | 0.9571 | 1.0000 | 0.9899 | 0.9831 | 0.9868 | 0.8487 | 0.9503 |
| FAMI | -0.0256 | 0.8689 | 0.8412 | 0.9574 | 0.9355 | 0.9428 | 0.9899 | 1.0000 | 0.9813 | 0.9907 | 0.8437 | 0.9416 |
| ORAL | -0.0120 | 0.9114 | 0.9068 | 0.9545 | 0.9506 | 0.9483 | 0.9831 | 0.9813 | 1.0000 | 0.9934 | 0.8912 | 0.9821 |
| WRIT | -0.0438 | 0.9088 | 0.8931 | 0.9593 | 0.9422 | 0.9461 | 0.9868 | 0.9907 | 0.9934 | 1.0000 | 0.8559 | 0.9676 |
| PHYS | 0.0542 | 0.7419 | 0.7887 | 0.8129 | 0.8795 | 0.8718 | 0.8487 | 0.8437 | 0.8912 | 0.8559 | 1.0000 | 0.9065 |
| RTEN | -0.0336 | 0.9373 | 0.9437 | 0.9300 | 0.9271 | 0.9250 | 0.9503 | 0.9416 | 0.9821 | 0.9676 | 0.9065 | 1.0000 |
从相关系数看,只有 CONT 变量跟其它变量没有相关性。
2.5 step3:计算特征值和特征向量
利用eigen函数计算相关系数矩阵的特征值和特征向量。
dat_eigen=eigen(dat_cor)
dat_var=dat_eigen$values ## 相关系数矩阵的特征值
options(digits=4, scipen=4)
dat_var
## [1] 10.133504 1.104147 0.332902 0.253847 0.084453 0.037286 0.019683
## [8] 0.015415 0.007833 0.005612 0.003258 0.002060
pca_var=dat_var/sum(dat_var)
pca_var
## [1] 0.8444586 0.0920122 0.0277418 0.0211539 0.0070377 0.0031072 0.0016402
## [8] 0.0012846 0.0006528 0.0004676 0.0002715 0.0001717
pca_cvar=cumsum(dat_var)/sum(dat_var)
pca_cvar
## [1] 0.8445 0.9365 0.9642 0.9854 0.9924 0.9955 0.9972 0.9984 0.9991 0.9996
## [11] 0.9998 1.0000
可以看出,PC1(84.4%)和PC2(9.2%)共可以解释这12个变量的93.6的程度,除了CONT外的其他的11个变量与PC1都有较好的相关性,所以PC1与这11个变量基本斜交,而CONT不能被PC1表示,所以基本与PC1正交垂直,而PC2与CONT基本平行,表示其基本可以表示CONT。
2.6 step4:崖低碎石图和累积贡献图
library(ggplot2)
p=ggplot(,aes(x=1:12,y=pca_var))
p1=ggplot(,aes(x=1:12,y=pca_cvar))
p+geom_point(pch=2,lwd=3,col=2)+geom_line(col=2,lwd=1.2)
p1+geom_point(pch=2,lwd=3,col=2)+geom_line(col=2,lwd=1.2)
崖低碎石图(scree plot)即贡献率图,是希望图形一开始很陡峭,如悬崖一般,而剩下的数值都很小,如崖底的碎石一样。
崖低碎石图和累积贡献率图是对主成分贡献率和累积贡献率的一种直观表示,用以作为选择主成分个数的参考。本例中第一个主成分解释总变异的84.4%,可以只选择第一个主成分,但第二主成分也不小,因此选择前两个主成分。
主成分的个数选择没有一定之规,需按实际情况具体分析,一般要求累积贡献率大于85%或特征值大于1.
但是在实际的生物信息学应用中,通常达不到这个要求。
2.7 step5:主成分载荷
主成分载荷表示各个主成分与原始变量的相关系数。
pca_vect= dat_eigen$vector ## 相关系数矩阵的特征向量
loadings=sweep(pca_vect,2,sqrt(pca_var),"*")
rownames(loadings)=colnames(USJudgeRatings)
options(digits=4, scipen=4)
kable(loadings[,1:2])
| CONT | 0.0028 | 0.2830 |
|---|---|---|
| INTG | -0.2652 | -0.0552 |
| DMNR | -0.2636 | -0.0599 |
| DILG | -0.2797 | 0.0110 |
| CFMG | -0.2780 | 0.0511 |
| DECI | -0.2774 | 0.0388 |
| PREP | -0.2843 | 0.0098 |
| FAMI | -0.2818 | -0.0004 |
| ORAL | -0.2874 | -0.0011 |
| WRIT | -0.2858 | -0.0095 |
| PHYS | -0.2580 | 0.0270 |
| RTEN | -0.2847 | -0.0119 |
结果表明,CONT指标跟其它指标表现完全不一样,第一个主成分很明显跟除了CONT之外的所有其它指标负相关,而第二个主成分则主要取决于CONT指标。
2.8 step6:主成分得分计算和图示
将中心化的变量dat_scale乘以特征向量矩阵即得到每个观测值的得分。
pca_score=as.matrix(dat_scale)%*%pca_vect
head(pca_score[,1:2])
## [,1] [,2]
## AARONSON,L.H. 0.5098 -1.7080
## ALEXANDER,J.M. -2.2676 -0.8508
## ARMENTANO,A.J. -0.2267 -0.2903
## BERDON,R.I. -3.4058 -0.5997
## BRACKEN,J.J. 6.5937 0.2478
## BURNS,E.B. -2.3336 -1.3563
将两个主成分以散点图形式展示,看看这些样本被这两个主成分是如何分开的
p=ggplot(,aes(x=pca_score[,1],y=pca_score[,2]))+geom_point(color=USJudgeRatings[,1],pch=USJudgeRatings[,2])
p
https://mmbiz.qpic.cn/mmbiz_png/cZNhZQ6j4wytdsnNenoKyYFGJJUTcgm3Eicuqs0GA0dyHv5mXZ0yibbrEFrMxjT9NLC9LtRsX8WQcNXeBYaJicDgg/640?wx_fmt=png&wxfrom=5&wx_lazy=1&wx_co=1
对于主成分分析,不同数据会有不同的分析方法,应具体情况具体分析。
总结一下PCA的算法步骤:
设有m条n维数据。
- 1)将原始数据按列组成n行m列矩阵X
- 2)将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
- 3)求出协方差矩阵
- 4)求出协方差矩阵的特征值及对应的特征向量
- 5)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
- 6)Y=PX即为降维到k维后的数据
PCA本质上是将方差最大的方向作为主要特征,并且在各个正交方向上将数据“离相关”,也就是让它们在不同正交方向上没有相关性。
PCA也存在一些限制,例如它可以很好的解除线性相关,但是对于高阶相关性就没有办法了,对于存在高阶相关性的数据,可以考虑Kernel PCA,通过Kernel函数将非线性相关转为线性相关,关于这点就不展开讨论了。另外,PCA假设数据各主特征是分布在正交方向上,如果在非正交方向上存在几个方差较大的方向,PCA的效果就大打折扣了。
最后需要说明的是,PCA是一种无参数技术,也就是说面对同样的数据,如果不考虑清洗,谁来做结果都一样,没有主观参数的介入,所以PCA便于通用实现,但是本身无法个性化的优化。
3 实战一
比如你要做一项分析人的糖尿病的因素有哪些,这时你设计了10个你觉得都很重要的指标,然而这10个指标对于你的分析确实太过繁杂,这时你就可以采用主成分分析的方法进行降维。10个指标之间会有这样那样的联系,相互之间会有影响,通过主成分分析后,得到三五个主成分指标。此时,这几个主成分指标既涵盖了你10个指标中的绝大部分信息,这让你的分析得到了简化(从10维降到3、5维)。
下面是442个糖尿病人相关的数据集,具体如下:
- x a matrix with 10 columns (自变量)
- y a numeric vector (因变量)
library(lars)
library(glmnet)
data(diabetes)
attach(diabetes)
summary(x)
## age sex bmi
## Min. :-0.10723 Min. :-0.0446 Min. :-0.09028
## 1st Qu.:-0.03730 1st Qu.:-0.0446 1st Qu.:-0.03423
## Median : 0.00538 Median :-0.0446 Median :-0.00728
## Mean : 0.00000 Mean : 0.0000 Mean : 0.00000
## 3rd Qu.: 0.03808 3rd Qu.: 0.0507 3rd Qu.: 0.03125
## Max. : 0.11073 Max. : 0.0507 Max. : 0.17056
## map tc ldl
## Min. :-0.11240 Min. :-0.12678 Min. :-0.11561
## 1st Qu.:-0.03666 1st Qu.:-0.03425 1st Qu.:-0.03036
## Median :-0.00567 Median :-0.00432 Median :-0.00382
## Mean : 0.00000 Mean : 0.00000 Mean : 0.00000
## 3rd Qu.: 0.03564 3rd Qu.: 0.02836 3rd Qu.: 0.02984
## Max. : 0.13204 Max. : 0.15391 Max. : 0.19879
## hdl tch ltg
## Min. :-0.10231 Min. :-0.07639 Min. :-0.12610
## 1st Qu.:-0.03512 1st Qu.:-0.03949 1st Qu.:-0.03325
## Median :-0.00658 Median :-0.00259 Median :-0.00195
## Mean : 0.00000 Mean : 0.00000 Mean : 0.00000
## 3rd Qu.: 0.02931 3rd Qu.: 0.03431 3rd Qu.: 0.03243
## Max. : 0.18118 Max. : 0.18523 Max. : 0.13360
## glu
## Min. :-0.13777
## 1st Qu.:-0.03318
## Median :-0.00108
## Mean : 0.00000
## 3rd Qu.: 0.02792
## Max. : 0.13561
dim(x)
## [1] 442 10
length(y)
## [1] 442
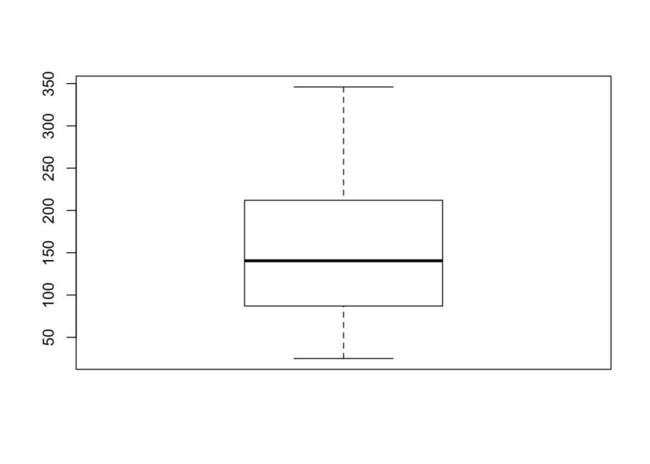
summary(y)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 25 87 140 152 212 346
boxplot(y)
其中x矩阵含有10个变量,分别是:“age” “sex” “bmi” “map” “tc” “ldl” “hdl” “tch” “ltg” “glu” 它们都在一定程度上或多或少的会影响个体糖尿病状态。
数据的详细介绍见 Efron, Hastie, Johnstone and Tibshirani (2003) “Least Angle Regression” (with discussion) Annals of Statistics;
一步法主成分分析
上面我们把整个主成分分析步骤拆解开来讲解具体原理,但是实际数据处理过程中我们通常是用现成的函数一步法完成主成分分析,而且这个是非常高频的分析,所以R里面自带了一个函数princomp()来完成主成分分析,如下:
data=x ## 这里的x是上面的 diabetes 数据集里面的 442个病人的10个生理指标
pca<-princomp(data, cor=FALSE)
cor是逻辑变量,当cor=TRUE表示用样本的相关矩阵R做主成分分析,当cor=FALSE表示用样本的协方差阵S做主成分分。
summary(pca)
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## Standard deviation 0.09542 0.05811 0.05223 0.04649 0.03871 0.03693
## Proportion of Variance 0.40242 0.14923 0.12060 0.09555 0.06622 0.06027
## Cumulative Proportion 0.40242 0.55165 0.67225 0.76780 0.83402 0.89429
## Comp.7 Comp.8 Comp.9 Comp.10
## Standard deviation 0.03484 0.03132 0.013311 0.0044009
## Proportion of Variance 0.05366 0.04337 0.007832 0.0008561
## Cumulative Proportion 0.94794 0.99131 0.999144 1.0000000
可以看到前三个主成份的信息量也只有67.2%,达不到我们前面说到85%,所以很难说可以用这3个主成分去代替这10个生理指标来量化病人的状态。
值得一提的是,如果你看懂了前面的主成分分析的拆解步骤,就应该明白有多少个变量就有多少个主成分,只是并不是所有的主成分都有意义,理想状态下我们希望有限的几个主成分就可以代替数量居多的变量,尤其是生物信息学里面的基因表达矩阵,两三万个基因的表达情况我们希望几十个基因就可以替代它们,因为那些基因之间是相互关联的。
碎石图
也可以画出主成分的碎石图,来决定选几个主成分。
screeplot(pca, type='lines')
由碎石图可以看出,第5个主成分之后,图线变化趋于平稳,因此可以选择前5个主成分做分析。
样本分布的散点图
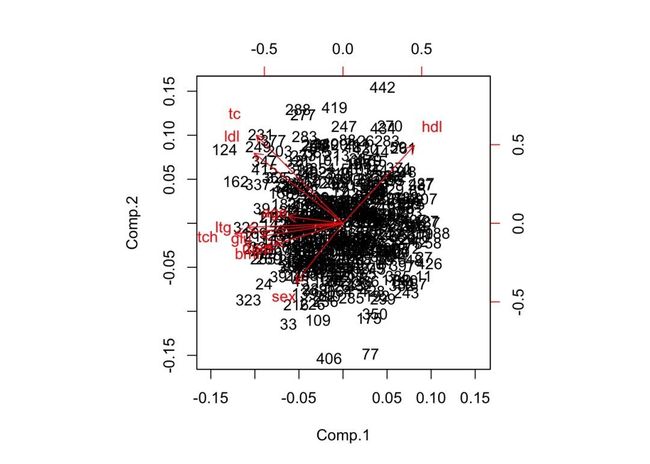
根据前两个主成分画出样本分布的散点图。
biplot(pca)
上面这个图似乎意义不大,因为大部分情况下都是需要结合样本的分组信息来看看这些主成分是否可以把样本比较不错的分开。
** 获得训练数据前4个主成份的值 **
kable(predict(pca, data)[1:4,])
| Comp.1 | Comp.2 | Comp.3 | Comp.4 | Comp.5 | Comp.6 | Comp.7 | Comp.8 | Comp.9 | Comp.10 |
|---|---|---|---|---|---|---|---|---|---|
| -0.0279 | -0.0926 | 0.0280 | 0.0039 | 0.0122 | 0.0481 | -0.0086 | -0.0360 | -0.0086 | -0.0023 |
| 0.1347 | 0.0653 | 0.0013 | 0.0224 | 0.0068 | 0.0482 | 0.0107 | 0.0090 | 0.0240 | 0.0021 |
| -0.0129 | -0.0778 | 0.0352 | 0.0376 | 0.0554 | 0.0529 | -0.0220 | -0.0401 | -0.0012 | -0.0026 |
| -0.0023 | 0.0182 | -0.0958 | -0.0653 | -0.0122 | -0.0212 | 0.0229 | 0.0175 | -0.0066 | -0.0035 |
kable(data[1:4,])
| age | sex | bmi | map | tc | ldl | hdl | tch | ltg | glu |
|---|---|---|---|---|---|---|---|---|---|
| 0.038076 | 0.050680 | 0.061696 | 0.021872 | -0.044223 | -0.034821 | -0.043401 | -0.002592 | 0.019908 | -0.017646 |
| -0.001882 | -0.044642 | -0.051474 | -0.026328 | -0.008449 | -0.019163 | 0.074412 | -0.039493 | -0.068330 | -0.092204 |
| 0.085299 | 0.050680 | 0.044451 | -0.005671 | -0.045599 | -0.034194 | -0.032356 | -0.002592 | 0.002864 | -0.025930 |
| -0.089063 | -0.044642 | -0.011595 | -0.036656 | 0.012191 | 0.024991 | -0.036038 | 0.034309 | 0.022692 | -0.009362 |
预测主成份的值,这里用的就是训练数据,所以得出训练数据主成分的值。
4 实战二
R中自带数据集data(Harman23.cor)数据集中包含305名受试者的8个身体测量指标
data(Harman23.cor)
kable(Harman23.cor[1:5])
## Warning in kable_markdown(x = structure(c("0", "0", "0", "0", "0", "0", :
## The table should have a header (column names)
## Warning in kable_markdown(x = structure("305", .Dim = c(1L, 1L), .Dimnames
## = list(: The table should have a header (column names)
5 进阶的主成分分析-psych包
正文中的princomp()函数为基础包中进行主成分分析的函数。 另外,R中psych包中提供了一些更加丰富有用的函数,这里列出几个相关度较高的函数,以供读者了解。
| 函数 | 描述 |
|---|---|
| principal() | 含多种可选的方差旋转方法的主成分分析 |
| fa() | 可用主轴、最小残差、加权最小平方或最大似然法估计的因子分析 |
| fa.parallel() | 含平行分析的碎石图 |
| factor.plot() | 绘制因子分析或主成分分析的结果 |
| fa.diagram() | 绘制因子分析或主成分的载荷矩阵 |
| scree() | 因子分析和主成分分析的碎石图 |
还有很多主成分分析结果可视化包,在直播我的基因组里面都提到过。
6 再推荐一个R包factoextra
factoextra是一个R包,易于提取和可视化探索性多变量数据分析的输出,包括:
- 主成分分析(PCA),用于通过在不丢失重要信息的情况下降低数据的维度来总结连续(即定量)多变量数据中包含的信息。
- 对应分析(CA)是适用于分析由两个定性变量(或分类数据)形成的大型应变表的主成分分析的扩展。
- 多重对应分析(MCA),它是CA对包含两个以上分类变量的数据表的适应。
- 多因素分析(MFA)专门用于数据集,其中变量被组织成组(定性和/或定量变量)。
- 分层多因素分析(HMFA):在将数据组织成层次结构的情况下,MFA的扩展。
- 混合数据因子分析(FAMD)是MFA的一个特例,专门用于分析包含定量和定性变量的数据集。
有许多R包实现主要组件方法。这些包包括:FactoMineR,ade4,stats,ca,MASS和ExPosition。然而,根据使用的包,结果呈现不同。为了帮助解释和多变量分析的可视化(如聚类分析和维数降低分析),所以作者开发了一个名为factoextra的易于使用的R包。
7.主成分分析的生物信息学应用
比如对千人基因组计划的对VCF突变数据进行主成分分析来区分人种:https://www.biostars.org/p/185869/
8. 主成分分析的其它可视化方法
看到一个包ropls 可视化做的不错,本来以为ropls 肯定是一个正常的r包,应该是在cran里面,结果
> install.packages('ropls')
Warning in install.packages :
package 'ropls' is not available (for R version 3.4.3)
Warning in install.packages :
cannot open URL 'https://cran.rstudio.com/bin/macosx/el-capitan/contrib/3.4/PACKAGES.rds': HTTP status was '404 Not Found'
> BiocInstaller::biocLite('ropls')
BioC_mirror: https://bioconductor.org
Using Bioconductor 3.6 (BiocInstaller 1.28.0), R 3.4.3 (2017-11-30).
Installing package(s) 'ropls'
trying URL 'https://bioconductor.org/packages/3.6/bioc/bin/macosx/el-capitan/contrib/3.4/ropls_1.10.0.tgz'
Content type 'application/x-gzip' length 1223650 bytes (1.2 MB)
==================================================
downloaded 1.2 MB
现在什么包都往bioconductor里面丢真奇怪。
后来仔细看标题,终于明白了。
ropls: PCA, PLS(-DA) and OPLS(-DA) for multivariate analysis and feature selection of omics data
构建就是组学数据
9.参考资料:
- http://www.cs.otago.ac.nz/cosc453/student_tutorials/principal_components.pdf
- https://www.cs.princeton.edu/picasso/mats/PCA-Tutorial-Intuition_jp.pdf
- http://www.cs.umd.edu/~samir/498/PCA.pdf
- http://www.yale.edu/ceo/Documentation/PCA_Outline.pdf
- http://people.tamu.edu/~alawing/materials/ESSM689/pca.pdf (R相关)
- http://www2.dc.ufscar.br/~cesar.souza/publications/pca-tutorial.pdf (2012)