图论——最小生成树 kurskal算法、prim算法

基本概念

树（Tree）

如果一个无向连通图中不存在回路，则这种图称为树。

生成树 （Spanning Tree）

无向连通图 $\mathrm{G}$ 的一个子图如果是一颗包含 $\mathrm{G}$ 的所有顶点的树，则该子图称为 $\mathrm{G}$ 的生成树。

生成树是连通图的极小连通子图。

这里所谓极小是指：若在树中任意增加一条边，则将出现一条回路；若去掉一条边，将会使之变成非连通图。

最小生成树

一个带权值的连通图，用 $n-1$ 条边把 $n$ 个顶点连接起来，使得连接起来的权值最小。

应用场景模拟

设想有9个村庄，这些村庄构成如下图所示的地理位置，每个村庄的直线距离都不一样。若要在每个村庄间架设网络线缆，若要保证成本最小，则需要选择一条能够联通9个村庄，且长度最小的路线。

Kruskal算法

前导知识点：并查集

基本思想

始终选择当前可用的且不会（和已经选取的边）构成回路的最小权植边。

具体步骤：

1. 将所有边按权值进行升序排序

2. 依次选择权值最小的边

3. 若该边的两个顶点落在不同的连通分量上，选择这条边，并把这两个顶点标记为同一连通分量；若这条边的两个顶点落到同一连通分量上，舍弃这条边。反复执行2,3，直到所有的都在同一连通分量上。【这一步需要用到上面的并查集】

模板题：https://www.luogu.org/problem/P3366

#include 
#include 
using namespace std;
int pre[5005];
int n, m; //n个定点，m条边

struct ENode {
     
    int from, to, dis;
    bool operator<(ENode p) {
     
        return dis < p.dis;
    }
}M[200005];

int Find(int x) {
     
    return x == pre[x] ? pre[x] : pre[x] = Find(pre[x]);
}

int kurskal() {
     
    sort(M, M + m);
    int N = n, res = 0;
    for (int i = 0; i < m && N > 1; i++) {
     
        int fx = Find(M[i].from), fy = Find(M[i].to);
        if (fx != fy) {
     
            pre[fx] = fy;
            N--;//找到了一条边，当N减到1的时候表明已经找到N-1条边了，就完成了
            res += M[i].dis;
        }
    }
    if (N == 1)//循环做完，N不等于1 表明没有找到合适的N-1条边来构成最小生成树
        return res;
    return -1;
}

int main() {
     
    cin >> n >> m;
    for (int i = 0; i <= n; i++) {
     
        pre[i] = i;
    }
    for (int i = 0; i < m; i++) {
     
        scanf("%d%d%d", &M[i].from, &M[i].to, &M[i].dis);;
    }
    int ans = kurskal();
    if (ans != -1)
        cout << ans << endl;
    else
        cout << "orz" << endl;
    return 0;
}

Prim算法

Prim算法思想：

首先将图的点分为两部分，一种是访问过的 $u$（第一个点任选），一种是没有访问过的 $v$

1: 每次找 $u$ 到 $v$ 的权值最小的边。

2: 然后将这条边中的 $v$ 中的顶点添加到 $u$ 中，直到 $u$ 中边的个数 $=$ 顶点数 $-1$

图解步骤：

维护一个$dis$数组，记录只使用已访问节点能够到达各未访问节点最短的权值。（和单源最短路径迪杰斯特拉算法很像）

初始值为节点1（任意一个都可以）到各点的值，规定到自己是0，到不了的是$inf$（定义一个特别大的数）。

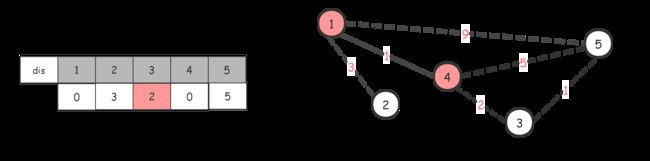
找当前能到达的权值最短的点。1–>4，节点4

将dis[4]赋值为0，标记为已访问过，同时借助4节点更新dis数组。

后面依次

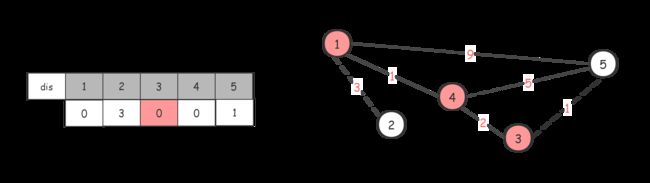
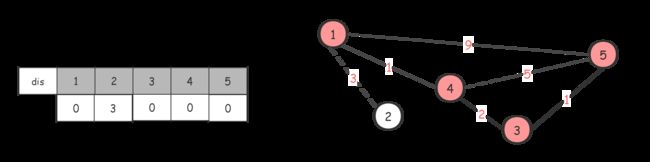
最后整个dis数组都是0了，最小生成树也就出来了，如果 $dis$ 数组中还有 $inf$ 的话，说明这不是一个连通图。

还是上面那道模板题：

#include 
#include 
using namespace std;

struct ENode {
     
    int dis, to;//权重、指向
    ENode* next = NULL;
    void push(int to, int dis) {
     
        ENode* p = new ENode;
        p->to = to; p->dis = dis;
        p->next = next;
        next = p;
    }
}*head;
const int inf = 1 << 30;
int N, M;
int dis[5005];

int prim() {
     
    int res = 0;
    for (int i = 2; i <= N; i++) 
        dis[i] = inf; 
    for (int i = 0; i < N; i++) {
     //与kurskal区分，找边是N-1条边，找点是N个点
        int v = 1 , MIN = inf;
        for (int j = 1; j <= N; j++) {
     
            //到不了的，访问过的不进行比较
            if (dis[j] != 0 && dis[j] < MIN) {
     
                v = j;
                MIN = dis[j];
            }
        }
        if (MIN == inf && v != 1)
        //这里v!=1是为了把dis的初始化放在循环里面做，也可以放在循环外面做，但是外层循环就只需要做N-1次了
            return -1;//还没找够n个点，没路了
        res += dis[v];
        dis[v] = 0;
        //借助第v个结点去更新dis数组
        ENode *p = head[v].next;
        while (p) {
     
            if (dis[p->to] > p->dis) {
     
                dis[p->to] = p->dis;
            }
            p = p->next;
        }
    }
    return res;
}

int main() {
     
    cin >> N >> M;
    head = new ENode[N + 1];
    for (int i = 0; i < M; i++) {
     
        int from, to, dis;
        scanf("%d%d%d", &from, &to, &dis);
        head[from].push(to, dis);
        head[to].push(from, dis);
    }
    int ans = prim();
    if (ans != -1)
        cout << ans << endl;
    else
        cout << "orz" << endl;
    return 0;
}

两者对比

时间复杂度

prim算法

时间复杂度为$O(n^2)$，$n$为顶点的数量，其时间复杂度与边得数目无关，适合稠密图。

kruskal算法

时间复杂度为$O(e\cdot loge)$，$e$为边的数目，与顶点数量无关，适合稀疏图。其实就是排序的时间，因为并查集的查询、合并操作都是$O(1)$。

总结

通俗点说就是，点多边少用Kruskal，因为Kruskal算法每次查找最短的边。 点少边多用Prim，因为它是每次找一个顶点。

具体选择用那个，可以用电脑算一下，题目给的数据级别，$n^2$和$e\cdot loge$看看那个小，比如上面的模板题，题目给的数据级别是$(n<=5000,e<=200000)$，粗略估算一下，kurskal算法一定是会快不少的，结果也确实如此。

实现难度

实现上kurskal算法要简单太多了。kurskal算法不需要把建图，而Prim算法必须建邻接表或者邻接矩阵，所以从上面的运行结果也能看出来当边的数目较大时，Prim算法所占用的空间比kurskal算法多了很多。

拓展

堆优化的Prim算法

用堆存储当前所有可到达的点和距离，就是把dis数组里的内容一式两份，存在堆里，然后每次取堆顶元素，每次操作为$O(logn)$，所以使用堆优化后的Prim算法理论上时间复杂度为$O(nlogn)$，但是好像没有达到想要的效果

看了测试数据发现，有很多重边，那就合理了，做了很多次的堆操作，所以时间上也和kurskal比较相近。所以在数据可靠、无重边的情况下，这个算法一定是上述几种中最快的一个。

#include 
#include 
#include 

using namespace std;
struct P {
     
    int dis, v;
    P(int d, int v) :dis(d), v(v) {
     };
    bool operator<(P p)const {
     
        return p.dis < dis;
    }
};
struct ENode {
     
    int dis, to;//权重、指向
    ENode* next = NULL;
    void push(int to, int dis) {
     
        ENode* p = new ENode;
        p->to = to; p->dis = dis;
        p->next = next;
        next = p;
    }
}*head;
const int inf = 1 << 30;
int N, M;
int dis[5005];

int prim() {
     
    priority_queue<P>pq;
    pq.push(P(0, 1));
    int res = 0, cnt = N;
    dis[1] = 0;
    fill(dis + 1, dis + N + 1, inf);

    while (!pq.empty() && cnt > 0) {
     //与kurskal区分，找边是N-1条边，找点是N个点
        int v = pq.top().v, d = pq.top().dis;
        pq.pop();
        if (!dis[v])continue;
        dis[v] = 0;
        res += d;
        cnt--;
        ENode* p = head[v].next;
        while (p) {
     
            if (dis[p->to] > p->dis) {
     
                dis[p->to] = p->dis;
                pq.push(P(p->dis, p->to));
            }
            p = p->next;
        }
    }
    if (cnt > 1)
        return -1;
    return res;
}

int main() {
     
    cin >> N >> M;
    head = new ENode[N + 1];
    for (int i = 0; i < M; i++) {
     
        int from, to, dis;
        scanf("%d%d%d", &from, &to, &dis);
        head[from].push(to, dis);
        head[to].push(from, dis);
    }
    int ans = prim();
    if (ans != -1)
        cout << ans << endl;
    else
        cout << "orz" << endl;
    return 0;
}