图论 —— 最小生成树(朴素Prim原理及模板题)
最小生成树
- 模板题
- 以模板题为例子解释
- AC代码:(代码有详细的注释!)
可供练习 总题单 week 3 [kuangbin带你飞] 题单 最小生成树 + 线段树 Click here ~~
https://blog.csdn.net/m0_46272108/article/details/108980362
模板题
给定一个n个点m条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出impossible。
给定一张边带权的无向图G=(V, E),其中V表示图中点的集合,E表示图中边的集合,n=|V|,m=|E|。
由V中的全部n个顶点和E中n-1条边构成的无向连通子图被称为G的一棵生成树,其中边的权值之和最小的生成树被称为无向图G的最小生成树。
输入格式
第一行包含两个整数n和m。
接下来m行,每行包含三个整数u,v,w,表示点u和点v之间存在一条权值为w的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出impossible。
数据范围
1 ≤ n ≤ 500 1≤n≤500 1≤n≤500,
1 ≤ m ≤ 1 0 5 1≤m≤10^5 1≤m≤105,
图中涉及边的边权的绝对值均不超过10000。
输入样例:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例:
6
以模板题为例子解释
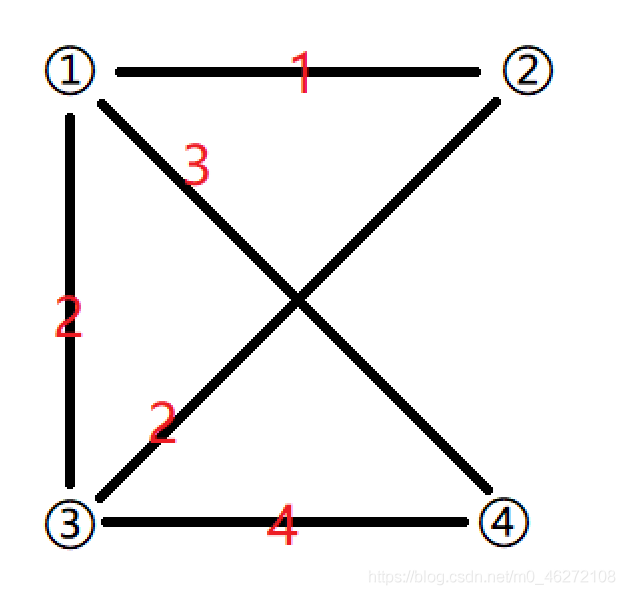
根据给出的案例如图所示:
将所有的点距离初始化为正无穷。

迭代n次 for (int i = 0; i < n; ++i ){ }
1.找到集合外最近的点,赋值为t
2.用t更新其他点到集合的距离(某一个点到集合的距离:这个点到集合内部的所有边当中的长度最短的边)
3.将t放到集合里面去 st[t] = true;
挑一个点放入集合中(这里挑①)

用这个点更新其它点到 集合 的距离。(看其它点有没有一条边能连向集合内部),则点②更新为1,点③更新为2,点④更新为3

在其它点(②③④)中,选一个距离集合(这里的集合只有点①)最近的点,即②,看是否能通过②这个点,更新其它点的距离,
①——②——③ 距离为3 大于 ①——③,所以不能更新,②没有到④的线,所以总体无变化 ,则把点②加到集合中去,此时①——②这条边是属于集合的一条边。
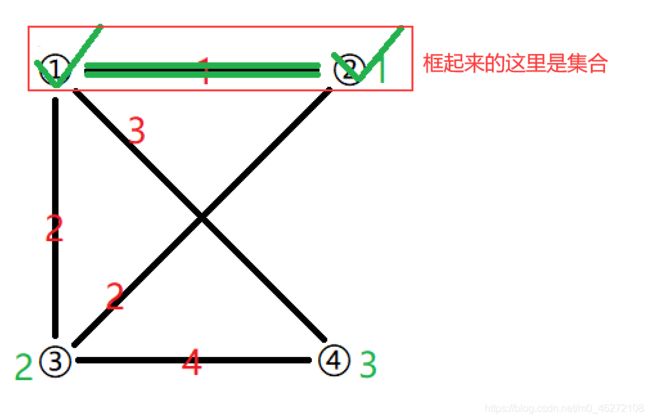
选下一个点③,①——④ 距离为3,①——③——④距离为6
总体无变化,将③加到集合中
由于①——③和②——③这两条边的距离相等,所以只选一条边加入即可。
最后把④也加入集合。
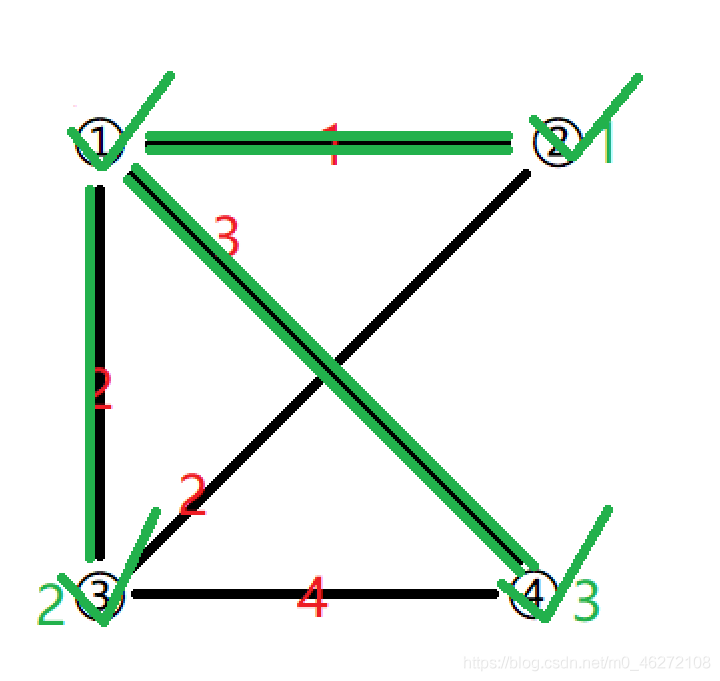
或者:

绿色的部分为集合。
生成树: 每次选中的这个点,它的距离对应的那条边就是生成树里的一条边。
最终这个集合就是这个案例最终的最小生成树。
最小生成树案例:
地图上有n个城市(已知坐标),要在城市之间铺设城际公路,使得城市与城市之间可以相互连通。问铺设城际公路最小的总长度是多少?
(最小生成树中正边和负边 ‘权重的正负’ 无关,都可以。)
(集合:代表当前已经在连通块的所有点)
AC代码:(代码有详细的注释!)
#includeCode Java
import java.lang.*;
import java.util.*;
public class Main {
static int N = 1010;
static int n, m;//n代表点,m代表边
static int [][] g = new int[N][N];//邻接矩阵
static int [] dist = new int[N];//距离
static int [] st = new int[N];//判断该点是否在集合内
public static int prim() {
Arrays.fill(st, 0);
//n次迭代
int res = 0;//存最小生成树里面所有长度之和
//初始化距离
for (int i = 1; i <= n; ++i) {
dist[i] = g[1][i];
}
for (int i = 1; i <= n; ++i) {
//找到集合外,距离最短的点
int t = -1;//初始化t == -1 表示我们当前还没有找到任何一个点。
for (int j = 1; j <= n; ++j) {
//在集合外,t == -1还没有找到任何一个点 || t的距离大于j的距离
if (st[j] == 0 && (t == -1 || dist[t] > dist[j])) {
t = j;//就把t 更新成 j
}
}
st[t] = 1;//将点加到树里面去。
/* 这里要先更新再累加,不然会出现自环问题,最小生成树是不存在环的。*/
//用t更新一下,其他点到 集合 的距离
for (int j = 1; j <= n; ++j) {
if (st[j] == 0) {
dist[j] = Math.min(dist[j], g[t][j]);
}
}
}
//如果只要不是第一个点,就把dist[t]加到最小生成树的长度和里面去。只要不是第一个点,dist[t]表示当前这个点和现在已经连好的生成树里面的某一条边的长度。而且dist[t]代表一条树边,所以加上就可以了
for (int i = 1; i <= n; ++i) {
res += dist[i];
}
return res;
}
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
while (input.hasNext()) {
n = input.nextInt();
if (n == 0) break;
m = input.nextInt();
int u, v, w;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
if (i==j) g[i][j] = 0;
else g[i][j] = 0x3f3f3f3f;//初始化为 +∞
}
}
//读入所有边
for (int i = 0; i < m; ++i) {
u = input.nextInt();
v = input.nextInt();
w = input.nextInt();
//无向图,就是建一条从a到b,再建一条从b到a的就可以了
g[v][u] = g[u][v] = Math.min(g[u][v], w);//可能有重边,求一个min即可
}
System.out.println(prim());
}
}
}