[医学小样本分割]Few-shot Medical Image Segmentation using a Global Correlation Network with Discriminative

基于判别嵌入的全局相关网络的Few-Shot医学图像分割

论文地址

摘要

我们利用片段式(episodi)训练的深度卷积网络构造我们的Few-Shot图像分割器。基于医学图像的空间一致性和规律性，我们开发了一个高效的全局相关模块来捕获支持和查询图像之间的相关性，并将其纳入到全局相关网络中。此外，我们还提高了深度嵌入的可鉴别性，以促进同一类特征域的聚类，同时使不同器官的特征域保持较远的距离。

存在的问题及解决方案

医学图像Few-Shot分割虽然具有重要的应用潜力，但其研究还相对缺乏。医学图像的Few-Shot分割不同于自然图像，有以下几个原因，这证明了特设模型的必要性：

首先，正确捕获成对查询和支持图像中前景的相关性在空间和语义上都是至关重要的。医学图像前景物体在强度、形态和结构上是一致的。如图1所示，脾脏(spleen)在不同的MR图像中表现出相似的强度，而肝脏(liver)在不同CT图像中表现出与肝脏血管相似的结构。相比之下，在自然图像中呈现的类可能包含更多的子概念，并显示出较大的类内变化。

此外，我们还观察了前景中查询和支持图像的空间非对齐性。在这方面，计算查询和支持图像的前景全局相关连接空间上距离较远的同一语义对象。在以往的方法中，对空间相关性的研究不够有效。例如，以往的方法通过掩码提取前景对象，并全局平均池化生成支持图像中该类的“原型”，然后利用度量将该原型与查询图像中的每个空间位置进行比较，以确定其分割。但这样掩码操作消除了上下文信息，全局平均池化丢弃了形状信息。 在使用空间激活方法的工作中，支持图像的空间信息在没有二进制掩盖和池化的情况下被保留，但是这种空间压缩和激活(sSE)注意模块要求支持图像和查询图像之间的前景空间重叠，以产生有意义的注意。

其次，除了前景一致性之外，与自然图像相比，医学图像中的上下文在不同图像之间的差异较小。在自然图像分割中，如果要分割一个类别为“狗”的对象，其中一只狗可能在一张图像中处于野外，另一只狗可能在家中。相比之下，医学图像中的某一类背景更具有一致性和规律性。 例如，以肝脏为目标的腹部图像，也很可能呈现出肾脏、脾脏等其他器官的相对位置，如图1所示。这种规律性形成了一种更具鉴别性的器官表征。通过在查询图像和支持图像之间施加较大的类间距离和较小的类内距离，将更有分辨力的知识转移到新类的分割中

本文提出了一种基于判别嵌入的全局相关网络的Few-Shot医学图像分割方法。利用卷积层将支持和查询图像投影到特征空间。将其嵌入域的深度特征转发到一个高效的全局相关模块中，分别计算长程和短程依赖关系，降低计算复杂度。在此基础上，对不同前景类图像的深度特征进行了区分性正则化，将同一前景类图像的深度特征拉近，将不同前景类图像的深度特征推远。实验结果表明，该方法的非局部模块、嵌入的判别正则化和切片选择提高了分割性能，在Few-Shot医学图像分割中达到了目前最先进的精度。

方法

Global Correlation Network

本工作使用了sSE来进行特征校准，但光使用这个是不够的。因为，sSE模块通常需要刚性的空间对齐，而在大多数场景下，精确对齐并不常见。因此，在位置模式被很好地保存的大规模特征上，捕获较长范围依赖性的方案是必要的。为了捕获整个特征图中的长范围依赖关系，我们将全局相关操作表述为：

函数$h(\cdot )$计算连接的深度特征$f_c$中位置$i$和$j$之间的相关性。$f_c\in R^{H\times W\times \left(C_q+C_s\right)}$是由查询特征$f_q\in R^{H\times W\times C_q}$和支持特征$f_s\in R^{H\times W\times C_s}$连接得到的，表示为$f_c=$ concate $\left[f_s;f_q\right]$。函数映射$g(\cdot )$对要加权的位置$j$处的级联深层特征的表示进行编码。

根据以往文献中提出的非局部模块，计算空间相关性$h(\cdot )$的复杂度随着H和W的相乘而二次增长，这在$f_c$的太大时是不可容忍的。然而，在小规模的深层语义空间中，语义被增强，空间信息被扭曲，非局部关系的使用受到限制。

基于这一分析，我们提出了一个高效的全局相关模块，如图3所示。实现捕获全局空间相关性和降低计算复杂度之间的平衡。

在图3(b)中，我们展示了远程和短程关联的工作流程。在远程相关建模中，固定步长的像素被提取并置换为一组远程表示。对该组的每个成员分别应用空间相关性计算。然后应用合并操作将像素恢复到其原始位置。在短程表示中，将整个特征空间划分为局部子区域来构造短程表示。然后在表示上计算相似空间相关性，并且它们被合并回原始形状。

接下来，我们实例化基于公式(1)中给出的思想构建的空间相关性。空间相关性的架构如图3©所示，输入特征$f_{in}\in R^{H\times W\times C}$通过由1×1×1卷积实现的线性变换$\theta$投影到嵌入空间以获得${\theta }_{1\times 1\times 1}\left(f_{in}\right)\in R^{H\times W\times C^{\prime }}$。类似地，使用另一个线性变换$\phi$完成相同的特征$f_{in}$嵌入${\phi }_{1\times 1\times 1}\left(f_{in}\right)\in R^{H\times W\times C^{\prime }}$。两个线性变换$\theta$和$\phi$融合了查询和支持图像的空间表示。我们根据经验设定$C^{\prime }$为$C$的一半。将这两个嵌入相乘得到一个全局相关矩阵$M_{gc}\in R^{HW\times HW}$：

其中$vec$表示向量化操作。全局相关矩阵的第$i$行$M_{cc}(i,:)$编码$f_{in}$中所有位置的贡献。全局相关矩阵$M_{gc}$的每一行由softmax函数归一化，表示为$S{M}_{row}(M_{gc})$。

另一个使用1 × 1 × 1卷积的线性变换$g$将级联特征映射到另一个嵌入$g_{1\times 1\times 1}\left(f_{in}\right)\in R^{H\times W\times C^{\prime }}$，我们将空间相关模块的输出$f_{\text{out }}\in R^{H\times W\times C}$表示为：

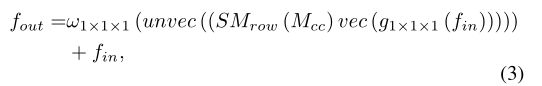
我们将高效的GC模块应用于第二和第三大规模的浅层，在这些浅层中保留了定位特征。我们在图4中展示了一组可视化的例子。分别以左肾、右肾和脾为靶器官。通过设计高效的全局相关模块，我们观察到查询特征中的前景器官得到了增强。

Discriminative Embedding

在不同的成像扫描中，器官的背景是一致的。除了前景器官之外，对于不同的图像，其他主要器官的强度和位置是规则的，在潜在特征空间中为每个器官形成不同的聚类。这种聚类以类内方式聚集，以类间方式远离。在测试阶段，使用判别性嵌入训练的模型可以实现对不可见类器官的更好分割，并抑制出现在其它主要器官区域的假阳性预测。

在训练数据集中，假定我们有一个支持图像$X_s\in D_{tr}$带有多类标签$Y_s$和一张查询图像$X_q\in D_{tr}$带有相同数量的标记类$Y_q$。通过标签二值化，我们可以有一组二进制带标签的支持图像${\left\{\left(X_q,Y_q^i\right)\right\}}_{i=1}^{|Y_q|-1}$。类似地，我们获得一组二进制标签的查询图像${\left\{\left(X_s,Y_s^j\right)\right\}}_{j=1}^{|Y_s|-1}$。然后，我们有$|Y_q|-1$组深度特征用于查询图像${\left\{f_q^i\right\}}_{i=1}^{|Y_q|-1}$和$|Y_s|-1$组深度特征用于支持图像${\left\{f_s^j\right\}}_{j=1}^{|Y_s|-1}$。为了提高深度嵌入的判别性，我们驱动$f_q^i$和$f_s^j$靠近，如果$i=j$的话（支持和查询图像有相同的前景），反之如果$i\ne j$驱动它们远离（支持和查询图像有不同的前景）。

我们以L2范数的形式对组织或器官使用类内和类间距离来实现这样的约束。假设一个类$i\in Y_q$，我们在这个类对象上定义类内(intra class)距离和类间(inter class)距离：

一个非负的阈值操作被用来保持距离的正性。然后定义判别性嵌入损失函数${\mathcal{L}}_{de}$：

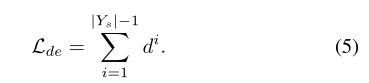
对支持特征和查询特征进行判别嵌入，如图2所示。在网络的后端放置正则化有助于保持像素级分类预测的可判别性。

实验结果

总结

在本研究中，我们提出一种有效的带鉴别嵌入的全局相关网络用于医学图像的Few-Shot分割。该模型的灵感来自于医学图像的几何和形态模式。全局关联模块有效地捕获支持查询图像对的前景关联。在特征空间中对同种器官进行分类，并对不同器官进行区分。在CT和MRI模式上的实验都被执行，以证明其最先进的分割精度。