机器学习 —— 李宏毅机器学习笔记（二）—— 回归问题
回归问题
机器学习笔记的第二篇博客，来介绍机器学习中最基础的回归任务，上一篇博客中有提到回归任务和分类任务的差别在于，回归任务中模型的输出是一个具体的数值， 而分类任务中模型的输出是某一类别。其实，许多问题我们都可以视为回归问题：
例如：根据股票市场的历史数据预测明天的股票走势；自动驾驶中根据传感器获取的信息输出方向盘的转动角度；推荐系统中，输入用户和商品的特征，模型输出一个[0,1]之间的数值，表示购买的可能性。
回归模型的建立
这里借用李宏毅老师课上的例子，预测宝可梦进化之后的CP值（战斗值），借助这个例子来回顾上一篇博客中介绍的机器学习模型建立的三个步骤：
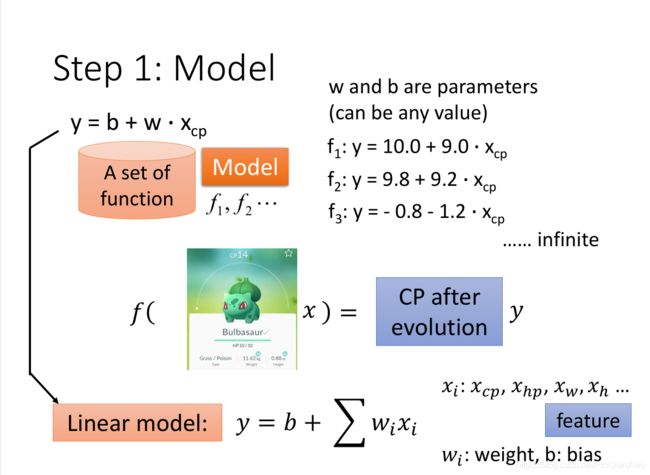
- 我们准备许多备选的函数 f ，构成一个集合，也就是机器学习中的模型（Model）。
- 使用训练数据来衡量这些备选函数的好坏程度。
- 根据训练数据选出拟合最好的函数，作为最终的拟合函数。
第一步：确定用于回归任务的模型
这里选择一元线性函数 y = wx + b即线性模型，一元表示我们使用的特征是一个（宝可梦的原CP值）；这样我们就构造了一个函数集合，由于参数w和b的取值是无穷的，所以函数集合中函数的个数是无穷个，接下来在函数集合中选择最好的函数的过程实际上就是为函数确定参数值的过程。
第二步：使用训练数据来衡量这些备选函数的好坏程度（确定参数）
接下来我们需要根据训练数据来从备选函数中选择一个效果最好的函数（即确定函数参数部分），这里需要使用损失函数，损失函数的输入是 “用来进行回归任务的函数” 和 “真实标签” ，输出是 进行回归任务的函数的好坏程度（Loss的值越小，认为该函数的效果越好）。如上图所示，我们使用 平方差之和 作为损失函数。
第三步：根据训练数据选出拟合最好的函数，作为最终的拟合函数
第三步，我们在训练数据上根据损失函数来评估拟合函数的好坏，找到使得损失函数最小的一组参数，作为我们最终的拟合函数。其中，寻找参数时，使用的方法为梯度下降法。
梯度下降
梯度下降算法是机器学习领域最广为人知、用途最广的优化算法，用来确定模型的参数（包括随机梯度下降SGD，Momentum，Adam等）。梯度下降算法的一个简单介绍如下：
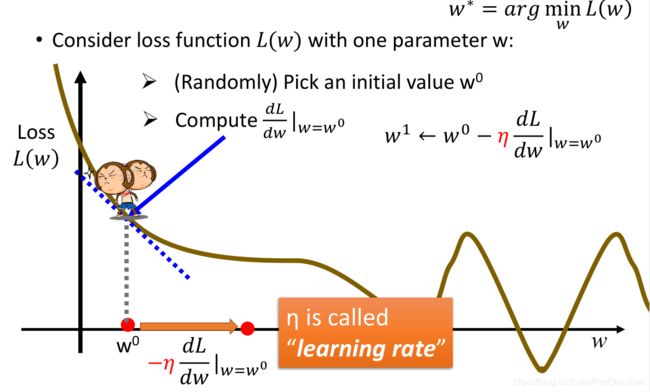
我们自定义的损失函数是关于参数的函数，以一个参数为例：L(w)。我们首先为w赋初始值w0，然后计算L(w)在w0处的导数，之后使用公式进行参数的更新：
，得到新的参数值w1。
以图片为例，如果导数是负值，我们增大参数；如果导数是正值，我们减小参数（所以w0更新到w1的过程是减法）。其中，
控制更新的幅度，被称为学习率。
1、在机器学习中，只要损失函数是可微分（可求导）的，就可以使用梯度下降算法进行参数的求解，那么怎么判断损失函数是否可微？（后面解释）
上面图片展示的是，模型当中只有一个参数（所以直接对该参数求导就可以），如果模型中存在两个及以上的参数，那么就需要分别对每个参数计算偏导数，然后根据参数更新公式进行每个参数的更新，如下图所示：
梯度下降算法的原理已经清楚，其实就是沿着损失函数降低的方向更新模型的参数，但是如果损失函数很复杂，比如下面图片所示，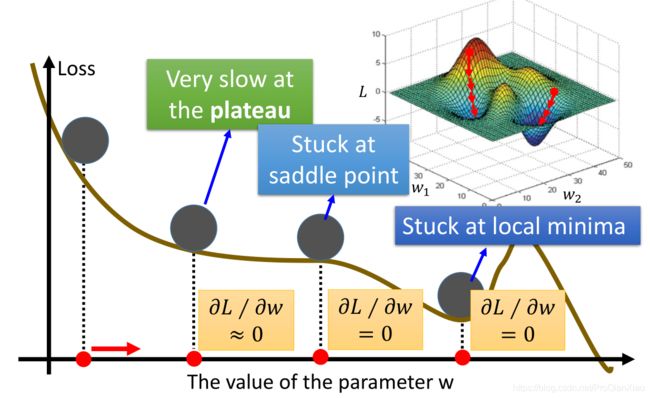
我们很可能在更新参数的过程中，走到导数为0的点（第四个红点位置），这时因为不知道更新的方向，就陷入了局部最优点（其实真正的全局最优点还在右边）。
2、不过对于上面回归问题中，损失函数为平方差之和，该损失函数为凸函数，没有局部最优点，只有全局最优点。那么如何判断一个函数是否为凸函数？（后面解释）
预测结果分析
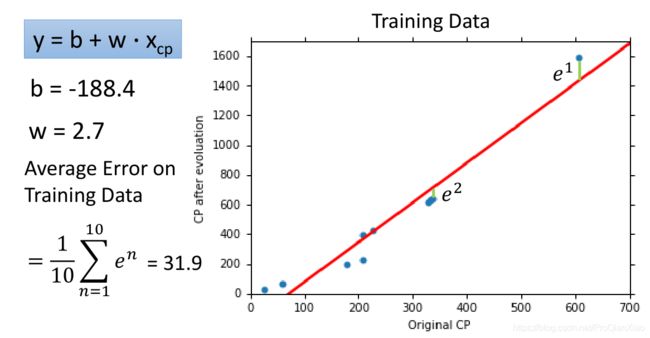
我们上面的线性模型，经过梯度下降算法，寻得一组最优参数，其结果表现如下：
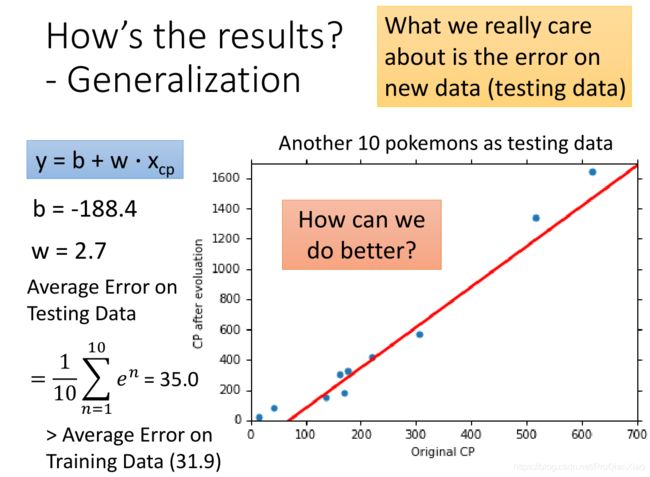
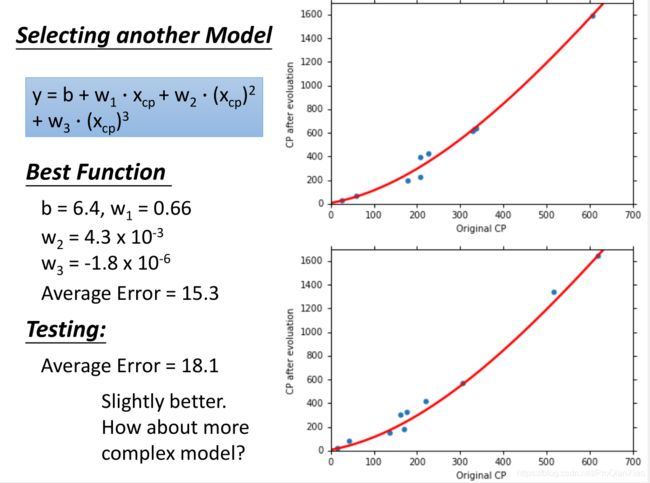
训练数据上面的损失函数值为31.9，测试数据上面损失函数值为35。在实际问题中，我们更加关注的是模型在测试集上面的性能表现，也就是模型的泛化能力，线性模型在测试集上面的误差较大，所以如果我们重新设计预测模型，使用更加复杂的模型，会不会得到更好的效果？
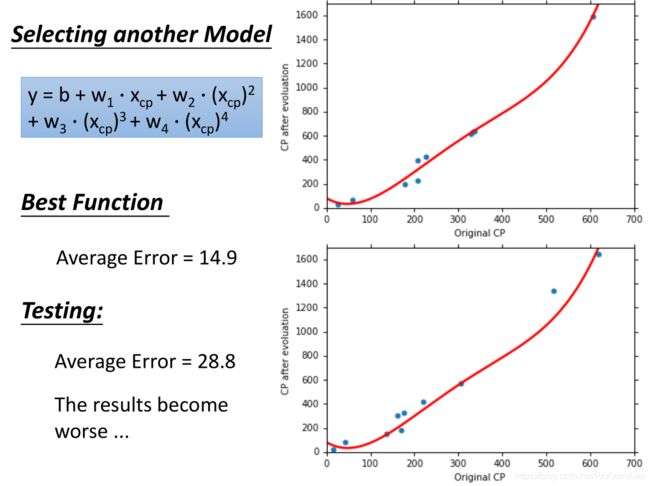
随着使用更加复杂的二次模型，三次模型，无论是在训练集还是测试集上面，效果都有提升。可是当继续增加模型的复杂度，使用四次模型的时候，虽然在训练集上面的loss更小，但是测试集上面的效果却变糟了。使用五次模型的时候，这一趋势更加明显：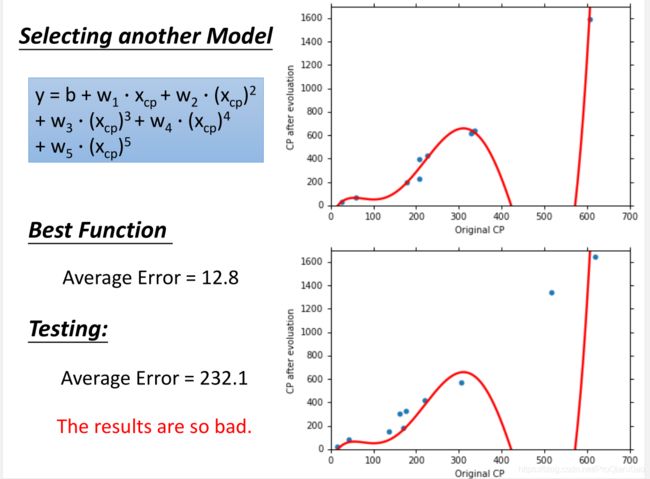
虽然复杂的模型对于训练数据的拟合程度会更好，但是很容易出现过拟合的现象（过于严格的去拟合训练数据，当面对新数据的时候没有办法做出准确的预测，即无法泛化到其他数据）。
在机器学习模型训练过程中，我们要尽量避免过拟合的现象，一方面要选择合适的模型，模型不是越复杂越好，可以通过交叉验证来选择合适的模型；另一方面，可以通过一些技术手段来帮助我们避免过拟合，比如正则化，early stopping等等。
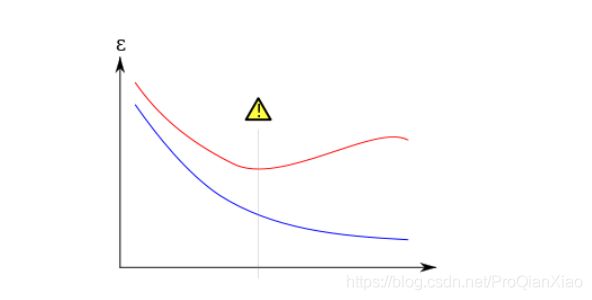
如上图所示，蓝色线代表训练集上的损失函数，红色线代表验证集的损失函数，当训练进行到中间垂直的线段时，模型应该是最优的；如果继续训练，就会造成过拟合现象。
正则化
简单来说，正则化是一种为了减小测试误差的行为(有时候会增加训练误差)。我们在构造机器学习模型时，最终目的是让模型在面对新数据的时候，可以有很好的表现。当使用比较复杂的模型比如神经网络，去拟合数据时，很容易出现过拟合现象(训练集表现很好，测试集表现较差)，这会导致模型的泛化能力下降，这时候，就需要使用正则化，降低模型的复杂度。
具体而言，正则化就是在损失函数后面增加一项惩罚项（对某些参数进行限制），使得我们的模型更加平滑。以上图为例，我们在损失函数后面增加一项关于参数w的正则项，限制参数w不要过大，这样模型会有更好的泛化能力。因为，这样对于测试数据中存在的噪声，会不那么敏感，即噪声对于预测的结果影响会降低。
假设，数据中存在的噪声为
，那么其在最终的预测结果中，产生的影响为，如果
的值较小，那么对于最终预测结果的影响也比较小。
注意，在正则化部分，我们只是添加了关于权重w的惩罚项，没有加入关于偏置b的惩罚项；因为从上面的分析，可以看出数据中的噪声产生的最终影响和偏置无关，如果从函数的角度分析，偏置不会影响函数的平滑程度，只会控制函数的上下移动。
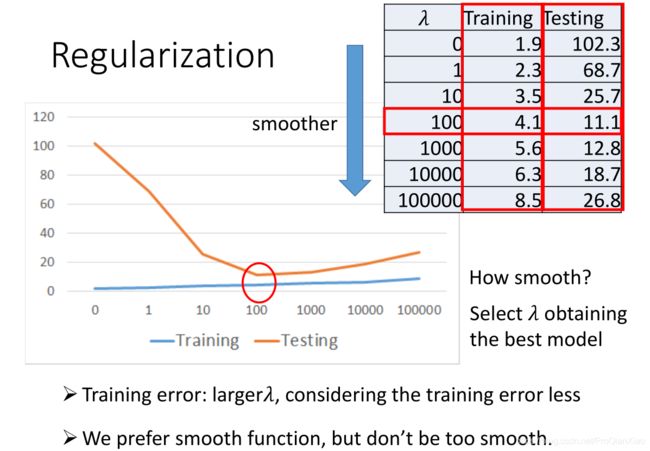
加入正则化技术之后，训练集和测试集上面的误差如下：
和我们的预期分析是一致的，加入正则化之后，参数
越大，表示我们越关注模型的平滑程度（也就是模型的泛化能力），相对于训练误差考虑较少，所以训练集上面的loss增大，测试集上面的loss降低。但是，参数不是越大越好，我们希望得到一个比较平滑的函数，但是不能过于平滑（会丧失其预测能力）。
遗留问题
1、在机器学习中，只要损失函数是可微的，就可以使用梯度下降算法进行参数的求解，那么怎么判断损失函数是否可微？（后面解释）
判断多元函数（损失函数中一般具有两个及以上的参数）是否可微，比较常用的方法是：证明该多元函数的偏导数存在且连续。
一般自己定义损失函数的时候，需要考虑这一点。大部分情况下，我们使用的是常见的损失函数。
2、不过对于上面回归问题中，损失函数为平方差之和，该损失函数为凸函数，没有局部最优点，只有全局最优点。那么如何判断一个函数是否为凸函数？（后面解释）
对于一元函数，我们直接求其二阶导数，如果二阶导数总是大于等于0，那么该一元函数为凸函数；
对于多元函数，我们需要首先求出该多元函数的海森矩阵（Hessian矩阵），如果其海森矩阵是半正定矩阵，那么该多元函数为凸函数。以上面回归问题中的损失函数为例：
判断一个矩阵是不是半正定矩阵，方法之一是判断该矩阵的所有主子式是不是非负；对于上面的海森矩阵，其所有主子式为：
，2, 0，均为非负，所以该海森矩阵为半正定矩阵。所以该损失函数为凸函数，只有全局最优值。