BP学习算法-构建三层神经网络

---

引：

    人工神经网络（Artificial Neural Networks，简写为ANNs）也简称为神经网络（NNs）或称作连接模型（Connection Model），是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。在人工神经网络发展的第二次热潮时期，1986年，鲁姆尔哈特（Rumelhart）和麦克劳（McCellan）等在《ParallelDistributedProcessing》中提出反向传播学习算法（B-P算法）。
    下面首先对神经网络做简单的介绍，然后再结合实例对B-P算法的原理和编程实现的步骤进行剖析，代码实现部分附在最后面。

---

正文：

[ 1 ]神经网络模型

    神经网络是一种模拟人脑的神经网络以期能够实现类人工智能的机器学习技术。人脑中的神经网络是一个非常复杂的组织。成人的大脑中估计有1000亿个神经元之多，它们彼此交织相连，可以完成学习、记忆、概括、推理等复杂工作。而人工神经网络也以神经元作为基本单位，在不断的训练过程中形成记忆，从而完成较为复杂的推理预测工作，其基本模型包括单层神经网络、多层神经网络以及全连接神经网络，如下图所示：

    图中的箭头可视为数据流，表示数据的输入、流向和输出；圆形是神经元，用于模拟人脑神经元的功能，具备一定的职能，对输入到该神经元的数据依据激励函数进行变换，得到输出值。单层神经网络很容易理解。多层神经网络稍微复杂，如上图中的两层神经网络，在进行数据处理时，输入层的的输出值作为隐含层的输入值，隐含层的输入值又会作为输出层的输入，层层递进。二而对于全连接型的网络运算情况就更为复杂，在此不作深入阐述。

---

[ 2 ]人工神经元模型

    下面来讨论一下“神经元”这个基本单元的构成及其工作方式。如下图所示：

    图中，Xi(t)，i=1,2,3,4,5作为该神经元模型的输入，w表示每个输入值对应的权值大小，两者经过乘积运算求和处理后被送入神经元Neuron i中；与阈值b经过某种映射变换f，最终得到输出值Yi(t)。这里的映射变换关系被称为作用在(b + ΣXi(t)*Wi)上的“激励函数”，即：三者之间存在的关系可表达为如下式子：

上式即可用于描述单个人工神经元的工作原理。
而关于激励函数（Transfer Function），也可称为传递函数，常用的激励函数包括：二值型函数、线性函数、S型函数等。在此不再进行详述，后面会有结合实例再次进行阐述。

---

[ 3 ]人工神经网络基本结构及其分类

    如下图所示为多层神经网络的基本结构，上面我们提到“人工神经网络也以神经元作为基本单位，在不断的训练过程中形成记忆，从而完成较为复杂的推理预测工作”,那么，这里的记忆就对应于权值个阈值。BP算法中，权值的修正是通过一个误差反向传播过程完成的，属于反馈型网络，但相应的，也有前向型网络，因此，在这里我们对前向型神经网络和反馈型神经网络进行一个简单区分。
①在前向型神经网络中，各神经元从输入层开始，接收前一级输入，并输出到下一级，直至输出层。整个网络中无反馈，可用一个有向无环图表示。
②而在反馈型神经网络中，每个神经元同时将自身的输出信号作为输入信号反馈给其他神经元，它需要工作一段时间才能达到稳定。其中全连接型神经网络就是后者的典型实例。

---

[ 4 ]监督学习与B-P神经网络

[ 4.1 ]监督学习

    监督学习也被称为“有师学习”，具体而言，就是需要提供训练集：{p1,t1}，{p2,t2}，......{p1,t1}，其中pi是输入，ti是输出。学习算法通过比较对应于每个输入的实际值和期望输出值，利用比较误差来调整整个网络的权值。其流程如下：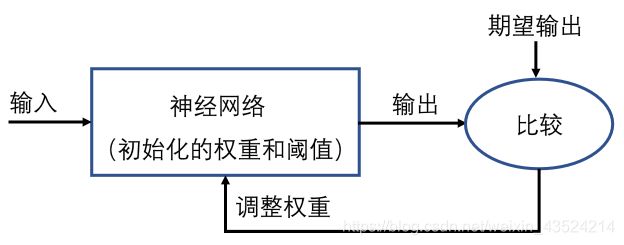

下面讨论的B-P学习算法的实现也属于有师学习范畴。但上述原理只是给出了在有输入值、实际输出值和期望输出值的条件下，进行权值调整的思路，但是对于多层神经网络中间的隐含层来说，它们并没有对应的可供参考的期望输出值，那么如何对隐含层发对应的权值进行调整？这就是下面在B-P算法中要讨论到的问题。

[ 4.2 ]B-P神经网络

    B-P神经网络，是一种按照误差逆向传播算法训练的多层前馈神经网络，它系统地解决了多层神经网络隐含层连接权学习问题，并在数学上给出了完整推导。 它的基本网络结构如下图，

对于基本神经元之间的变换关系，在[ 2 ]人工神经元模型中已经做过叙述，下面，我们来看一下B-P神经网络的工作过程，即：从训练集到最终预测结果这中间经过的两大步骤。这也是之后我们在具体实例中求解问题的主要思路框架。
⚫第一阶段或网络训练阶段：给定N组输入样本：xi=[xi1,xi2,…,xip1]T
                                                                输出样本：di=[di1,di2,…,din]，Ti=1,2,…,N
    通过针对输入集和输出集的训练，对网络的连接权进行学习和调整，以使该网络实现给定样本的输入输出映射关系。
⚫第二阶段或称工作阶段：把实验数据或实际数据输入到网络，网络在误差范围内预测计算出结果。

---

[ 4.3 ]B-P学习算法基本原理

    利用BP学习算法进行问题求解时，主要经历一下几个步骤：

➢正向传播：输入样本——输入层——各隐含层——输出层，主要是为了通过输入值和权值以及激励函数获取每一层对应的实际输出值；
➢判断是否转入误差反向传播阶段：若输出层的实际输出与期望输出不符，则反向传播误差;
➢误差反传：误差以某种形式在各层表示——根据误差结果进行各层的权值调整；
➢终止条件：网络输出的误差达到可以接受的程度或则达到预先设定的学习次数

---

[ 4.4 ]B-P学习算法权值调整方式

    权值调整也是BP算法关注的核心问题，下图中：Xji表示当前第n层的实际输入值，也就是第(n-1)层的实际输出值。
    ΔWji表示的是权值调整量，计算出权值调整量之后，在原先的权值基础上加上该调整量ΔWji即可得到修正后的权值。这在后面的代码中都有体现。

---

---

[ 5 ]问题描述与代码求解

[ 5.1 ]问题描述

※下表为某药品的销售情况，构造一个如下的三层神经网络对药品销售进行预测。

月份	1	2	3	4	5	6
销量	2056	2395	2600	2298	1634	1600
月份	7	8	9	10	11	12
销量	1873	1478	1900	1500	2046	1556

要求：设计如下图所示的三层人工神经网络，采用滚动预测方式，即用前三个月的销售量来预测第四个月的销售量：如用1、2、3月的销售量为输入预测第4个月的销售量，用2、3、4月的销售量为输入预测第5个月的销售量，如此反复直至满足预测精度要求为止。

---

[ 5.2 ]思路分析

【1】原始数据归一化处理。为方便后续计算，将原始数据用一维数组存放后进行归一化处理；
【2】数据分组。通过数据分组确定训练集和输出值；
【3】初始化权重值。这一步可通过随机数生成函数来实现，为方便运算，最好生成0-1之间的浮点型随机数作为权值；
【4】构建神经网络。主要是确定每一层在激励函数控制下的运算规则，以确定输出值；
【5】确定训练次数和误差阈值；
【6】开始训练，直到达到预定训练次数或者小于指定误差阈值就终止；
【7】利用训练数据检验训练结果，并进行下一年的1月份销售额的预测。

---

[ 5.3 ]代码实现

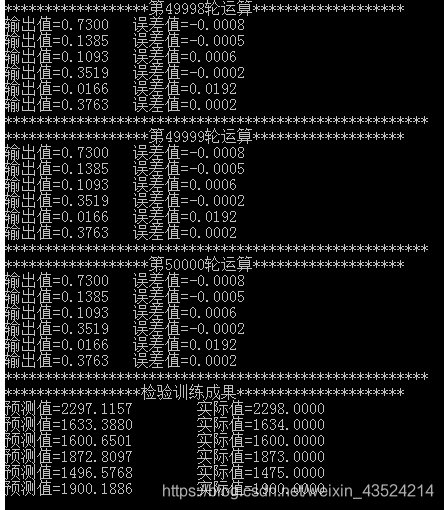
先上一张经过50000次训练后得到的误差值和检验训练结果的截图（所设置的学习常数的不同，对应的学习效率也会有所差别）

下面是具体的实现代码，针对于每步所作的操作附有注释。

#include
#include 
#include 
#include

/*
	神经网络输入层有三个结点，隐含层有5个节点，隐含层的激活函数为tansig；输出层有1个结点，激活函数为logsig。
	利用此网络对药品的下一年1月份销售量进行预测。
	原始数值归一化处理结果：
	【1】输入值：
	0.5152  0.8173  1.0000
	0.8173  1.0000  0.7308
	1.0000  0.7308  0.1390
	0.7308  0.1390  0.1087
	0.1390  0.1087  0.3200
	0.1087  0.3520  0.0000
	【2】期望输出值
	0.7308  0.1390  0.1087  0.3520  -0.0027 0.3761
*/

#define η 0.1	//学习常数
#define N 12	//数组元素个数
#define P_ROW 6	//行数（总的训练数据组数）
#define P_COL 3	//列数（每一组训练数据中的数据个数）
#define OUT_NUM 6//输出值个数
#define ih_ROW 5	//第1层权值矩阵行数
#define ih_COL 3	//第1层权值矩阵列数
#define ho_Col 5	//第2层权值矩阵列数
#define hiddenNum 5	//隐含层的值个数

double findMaxVal(double X[N], int size);//获取最大值
double findMinVal(double X[N], int size);//获取最小值
void normalizationData(double pData[P_ROW][P_COL], int row, int col);//归一化处理
void initWeightMatrix(double WeightVal_ih[ih_ROW][ih_COL], double WeightVal_ho[ho_Col]);//初始化权值矩阵:生成0-1之间得权值
void forwardProcessing(double inputVal[3], double hiddenVal[hiddenNum], double* outputVal);//正向处理数据
void adjustWeightMatrix(double ExpVal, double* outputVal, double WeightVal_ho[ho_Col], double hiddenVal[hiddenNum], double WeightVal_ih[ih_ROW][ih_COL], double inputVal[3]);//4、误差逆向传播-调整权值矩阵
double tansig(double Val);//隐含层激励函数
double logsig(double Val);//输出层激励函数
double reverseTrans(double normalVal);//从归一化指数逆变换为原数值


//初始数据数组：12个月份的对应值
double X[N] = {
      2056, 2395, 2600, 2298, 1634, 1600,
				1873, 1478, 1900, 1500, 2046, 1556 };
//训练数据:6组
double pData[P_ROW][P_COL] = {
      {
      2056, 2395, 2600 },
								{
      2395, 2600, 2298 },
								{
      2600, 2298, 1634 },
								{
      2298, 1634, 1600 },
								{
      1634, 1600, 1837 },
								{
      1600, 1873, 1478 } };
//输出的期望值:6个
double OutData[OUT_NUM] = {
      2298, 1634, 1600, 1873, 1475, 1900 };
//第1层权值数组：5*3
double WeightVal_ih[ih_ROW][ih_COL];
//第2层权值数组：1*5
double WeightVal_ho[ho_Col];
//隐含层的值:1*5
double hiddenVal[hiddenNum];
//输出层的值
double outputVal=0;


int main(int args, char* argv[])
{
     
	printf("人工神经网络预测模型\n");
	//【1】数据预处理
	srand((unsigned int)time(NULL));
	normalizationData(pData, P_ROW, P_COL);//1、归一化处理数据
	initWeightMatrix(WeightVal_ih, WeightVal_ho);//2、初始化权值矩阵

	//【2】、开始训练数据
	double *inputVal =NULL;//数据游标，控制训练数据组下标不断后移
	double ExpVal = 0;//记录期望输出值
	int count = 1;//计数器
	while (count<=50000)//这里只是设定了对训练次数的要求，对于误差限定，可使用一个数组记录每一轮得到的误差值进行限定
	{
     
		printf("******************第%d轮运算*******************\n",count);
		for (int i = 0; i < P_ROW; i++)
		{
     
			inputVal = pData[i];//用一级指针代替一维数组作为参数传递
			ExpVal = OutData[i];//记录当前次处理结果的期望输出值
			forwardProcessing(inputVal, hiddenVal, &outputVal);//3、正向处理数据
			adjustWeightMatrix(ExpVal, &outputVal, WeightVal_ho, hiddenVal, WeightVal_ih, inputVal);//4、逆向传播误差，修改权值
			printf("输出值=%.4f\t误差值=%.4f\n", outputVal, (outputVal - ExpVal));
		}
		count++;
		printf("*****************************************************\n");
	}

	//【3】检验训练成果
	printf("*****************检验训练成果*********************\n");
	double Data[P_ROW][P_COL] = {
      {
      2056, 2395, 2600 },
								{
      2395, 2600, 2298 },
								{
      2600, 2298, 1634 },
								{
      2298, 1634, 1600 },
								{
      1634, 1600, 1837 },
								{
      1600, 1873, 1478 } };
	double realData[OUT_NUM] = {
      2298, 1634, 1600, 1873, 1475, 1900 };
	normalizationData(Data, P_ROW, P_COL);
	for (int i = 0; i < P_ROW; i++)
	{
     
		inputVal = Data[i];//用一级指针代替一维数组作为参数传递
		forwardProcessing(inputVal, hiddenVal, &outputVal);//3、正向处理数据
		printf("预测值=%.4f\t实际值=%.4f\n", reverseTrans(outputVal), realData[i]);
	}
	//【4】利用训练结果预测数据
	printf("\n*****************利用训练结果预测数据*********************\n");
	//1500, 2046, 1556,归一化处理后对应数值为：[最大值-2600，最小值1478]
	double predictData[1][3] = {
      {
      1500, 2046, 1556 } };
	//归一化处理
	normalizationData(predictData, 1, 3);//归一化处理
	//得到隐含层的值
	forwardProcessing(predictData, hiddenVal, &outputVal);
	printf("最终预测得到归一化值为:%.4f\n对应下一年1月份销售额为:%.4f,", outputVal, reverseTrans((outputVal)));
	system("pause");
	return 0;
}

//从归一化指数逆变换为原数值
double reverseTrans(double normalVal)
{
     
	double maxVal = findMaxVal(X,N);
	double minVal = findMinVal(X,N);
	return normalVal*(maxVal - minVal) + minVal;
}

//1、归一化处理
void normalizationData(double pData[P_ROW][P_COL], int row, int col)
{
     
	//printf("归一化处理结果\n");
	int i, j;
	double maxVal = findMaxVal(X, N);//寻找最大值
	double minVal = findMinVal(X, N);//寻找最小值
	//printf("maxVal=%.2f\nminVal=%.2f\n", maxVal,minVal);
	//【1】归一化处理输入数据
	for (i = 0; i < row; i++)
	{
     
		for (j = 0; j < col; j++)
		{
     
			pData[i][j] = (pData[i][j] - minVal) / (maxVal - minVal);
			//printf("%.4f\t", pData[i][j]);
		}//end for-内
		//printf("\n");
	}//end for-外
	//printf("\n");
	//【2】归一化处理输出数据：OutData[OUT_NUM]
	for (i = 0; i < OUT_NUM; i++)
	{
     
		OutData[i] = (OutData[i] - minVal) / (maxVal - minVal);
		//printf("%.4f\t", OutData[i]);
	}
}

//2、初始化权值矩阵:生成0-1之间得权值
void initWeightMatrix(double WeightVal_ih[ih_ROW][ih_COL], double WeightVal_ho[ho_Col])
{
     
	//printf("初始化权重矩阵\n");
	int i, j;
	//初始化第一层权值矩阵：5*3
	for (i = 0; i < ih_ROW; i++)
	{
     
		for (j = 0; j < ih_COL; j++)
		{
     
			WeightVal_ih[i][j] = rand() / (RAND_MAX + 1.0);
			//printf("%.4f\t", WeightVal_ih[i][j]);
		}
	//	printf("\n");
	}
	//初始化第二层权值矩阵：1*5
	for (i = 0; i < ho_Col; i++)
	{
     
		WeightVal_ho[i] = rand() / (RAND_MAX + 1.0);
		//printf("w[%d]=%.4f\t",i,WeightVal_ho[i]);
	}
}

//3、正向处理数据:输入值->隐含层
void forwardProcessing(double inputVal[3], double hiddenVal[hiddenNum], double* outputVal)
{
     
	//printf("正向处理\n");
	int i, j,k;
	//【1】计算得到5个隐含层的值
	double sum_ih = 0.0;
	for (i = 0; i < hiddenNum;i++)//控制得到隐含层值必要的计算层数：5
	{
     
		for (j = 0; j < 3;j++)//求和：权重*输入值
		{
     
			sum_ih += inputVal[j] * WeightVal_ih[i][j];
		}
		hiddenVal[i] = tansig(sum_ih);//第i个输出的隐含层
		//printf("%.4f\t",hiddenVal[i]);
		sum_ih = 0;//将刻度值重置为0
	}
	//printf("\n");
	//【2】计算得到1个输出层的值-单个外层循环，可省略
	double sum_ho = 0.0;
	for (j = 0; j < hiddenNum;j++)
	{
     
		sum_ho += hiddenVal[j] * WeightVal_ho[j];
	}
	*outputVal = logsig(sum_ho);//输出层的值
	//printf("%.4f\n",*outputVal);
}

//4、误差逆向传播-调整权值矩阵
void adjustWeightMatrix(double ExpVal, double* outputVal, double WeightVal_ho[ho_Col], double hiddenVal[hiddenNum], double WeightVal_ih[ih_ROW][ih_COL], double inputVal[3])
{
     
	//printf("逆向处理\n");
	int i, j;
	double dt_oh;//权值的改正参数
	double dW_oh;//权值的改正值
	//【1】调整第2层权值
	double RealVal = *outputVal;
	dt_oh = RealVal*(1 - RealVal)*(ExpVal - RealVal);//权值改正值的参数
	for (i = 0; i < hiddenNum;i++)
	{
     
		dW_oh = η*dt_oh*hiddenVal[i];//权值改正值
		//printf("%.8f\t",dW_oh);
		WeightVal_ho[i] += dW_oh;//改正后权值

	}
	//printf("\n");
	//【2】调整第1层权值：5*3*个
	double dt_hi;
	double dw_hi;
	double realVal;
	for (i = 0; i < hiddenNum;i++)//5个改正值参数
	{
     
		realVal = hiddenVal[i];
		dt_hi = realVal*(1 - realVal)*dt_oh*WeightVal_ho[i];
		for (j = 0; j < 3;j++)
		{
     
			dw_hi = η*dt_hi*inputVal[j];//权值改正值
			WeightVal_ih[i][j] += dw_hi;//改正后权值
		}
	}
}

//获取最大值
double findMaxVal(double X[N], int size)
{
     
	int i, maxVal = X[0];
	for (i = 1; i < size; i++)
	{
     
		if (X[i]>maxVal)
		{
     
			maxVal = X[i];
		}
	}
	return maxVal;
}

//获取最小值
double findMinVal(double X[N], int size)
{
     
	int i, minVal = X[0];
	for (i = 1; i < size; i++)
	{
     
		if (X[i] < minVal)
		{
     
			minVal = X[i];
		}
	}
	return minVal;
}

//隐含层激励函数
double tansig(double Val)
{
     
	/*
	double exp(double x)
	返回 e 的 x 次幂的值*/
	return  ((2 / (1 + exp(-2 * Val))) - 1);
}

//输出层激励函数
double logsig(double Val)
{
     
	return 1 / (1 + (exp(-1 * Val)));
}

---

结束：

    好了，分享到这里就结束了，以上内容来是所学建模课程实验内容的延申。谈一谈这中间的感悟就是：在使用BP算法求解实际问题时，我觉得最重要的还是得先理清思路，弄清楚每一步要干什么，比如：这一步需要什么样的输入，经过带入激励函数完成变换后，会产生什么样的输出，这个输出值对问题求解有什么意义。然后就是使用代码去实现这些想法了。但如果对问题确实没有什么明确的思路，也可以尝试着一边理解一边编写代码去实现，只不过最终实现之后将代码重新整理一遍就是了。
    在此也作出说明：上述内容仅为个人对B-P学习算法的一些愚见，所附代码是针对上面实例所写，并不具备通用性，仅供参考。对于其他问题的求解，部分代码仍需结合实际情况自行修改。请大家多多指教！