09-LinearRegression线性回归和逻辑斯蒂回归

一.导数

• 几种常见函数的导数

① C'=0(C为常数)；
② (x^n)'=nx(n-1) (n∈Q)；
③ (sinx)'=cosx；
④ (cosx)'=-sinx；
⑤ (e^x)'=ex；
⑥ (a^x)'=axIna （ln为自然对数）
⑦ loga(x)'=(1/x)loga(e)

• 导数的四则运算

①(u±v)'=u'±v'
②(uv)'=u'v+uv'
③(u/v)'=(u'v-uv')/ v^2
④[u(v)]'=[u'(v)]*v' （u(v)为复合函数f[g(x)]）

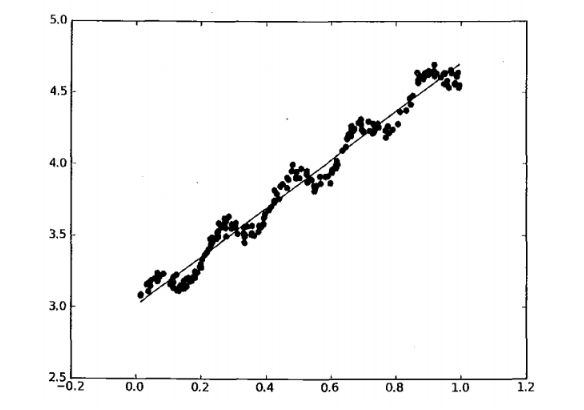
二.线性回归

• 最小二乘法

  
  
  

  二乘法1.png
  
  
  

  二乘法2.png

二乘法2.1.png

二乘法2.2.png

• 线性

得名于f(x)=ax+b的图像的形象 很直观 就是一条直线的形象

• 原理图

  
  
  

  线性原理图.png

实例糖尿病线性回归

1.导入相应包

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.linear_model import LinearRegression

2.读取文件数据

diabetes = datasets.load_diabetes() #糖尿病的信息

3.处理数据

#获取索引是2的数据
diabetes_X = diabetes.data[:,np.newaxis,2]

diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]

diabetes_Y = diabetes.target

diabetes_Y_train = diabetes_Y[:-20]
diabetes_Y_test = diabetes_Y[-20:]

4.训练线性回归算法

regr = LinearRegression()

# 第1步：训练
regr.fit(diabetes_X_train,diabetes_Y_train)

5.预测数据并绘制

plt.scatter(diabetes_X_test,diabetes_Y_test,color = 'black')

plt.plot(diabetes_X_test,regr.predict(diabetes_X_test),color = 'blue',lw = 3)

plt.show()

糖尿病.png

三.矩阵

• 满秩矩阵

满秩矩阵（non-singular matrix）: 设A是n阶矩阵, 若r（A） = n, 则称A为满秩矩阵。但满秩不局限于n阶矩阵。若矩阵秩等于行数，称为行满秩；若矩阵秩等于列数，称为列满秩。既是行满秩又是列满秩则为n阶矩阵即n阶方阵。行满秩矩阵就是行向量线性无关，列满秩矩阵就是列向量线性无关；所以如果是方阵,行满秩矩阵与列满秩矩阵是等价的。
满秩有行满秩和列满秩，既是行满秩又是列满秩的话就一定是是方阵

• 奇异矩阵

奇异矩阵是线性代数的概念，就是该矩阵的秩不是满秩。首先，看这个矩阵是不是方阵（即行数和列数相等的矩阵。若行数和列数不相等，那就谈不上奇异矩阵和非奇异矩阵）

a = np.array([[3,3.5,2],[3.2,3.6,3],[6,7,4]])
np.linalg.matrix_rank(a)

• 矩阵求逆

AA-¹=A-¹A=E（单位矩阵）
http://jingyan.baidu.com/album/1709ad8095e1924634c4f03a.html

• 逆矩阵作用

逆矩阵是经常遇到的一个概念。教科书中讲解了逆矩阵的求法，但是没有说清楚为何需要逆矩阵，逆矩阵的意义是什么。逆矩阵可以类比成数字的倒数，比如数字5的倒数是1/5，矩阵A的“倒数”是A的逆矩阵。5(1/5)=1, A（A的逆矩阵） = I，I是单位矩阵。引入逆矩阵的原因之一是用来实现矩阵的除法。比如有矩阵X，A，B，其中XA = B，我们要求X矩阵的值。本能来说，我们只需要将B/A就可以得到X矩阵了。但是对于矩阵来说，不存在直接相除的概念。我们需要借助逆矩阵，间接实现矩阵的除法。具体的做法是等式两边在相同位置同时乘以矩阵A的逆矩阵，如下所示，XA（A的逆矩阵）= B（A的逆矩阵）。由于A（A的逆矩阵） = I，即单位矩阵，任何矩阵乘以单位矩阵的结果都是其本身。所以，我们可以得到X = B（A的逆矩阵）。

• numpy矩阵求逆

a_ = np.linalg.inv(a)

四.岭回归

• 原理

  
  
  

  岭回归原理.png

• 缩减系数来“理解”数据

  
  
  

  图1.png
• 优点

缩减方法可以去掉不重要的参数，因此能更好地理解数据。此外，与简单的线性回归相比，缩减法能取得更好的预测效果;
岭回归是加了二阶正则项的最小二乘，主要适用于过拟合严重或各变量之间存在多重共线性的时候，岭回归是有bias的，这里的bias是为了让variance更小。

• 过拟合

过拟合即是过分拟合了训练数据，使得模型的复杂度提高，泛化能力较差（对未知数据的预测能力）
下面左图即为欠拟合，中图为合适的拟合，右图为过拟合。

过拟合.png

• 总结

1.岭回归可以解决特征数量比样本量多的问题
2.岭回归作为一种缩减算法可以判断哪些特征重要或者不重要，有点类似于降维的效果
3.缩减算法可以看作是对一个模型增加偏差的同时减少方差

• 应用场景

1.数据点少于变量个数
2.变量间存在共线性（最小二乘回归得到的系数不稳定，方差很大）
3.应用场景就是处理高度相关的数据

实例

1.导入

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression #普通线性回归
from sklearn.linear_model import Ridge #岭回归

2.假数据

x = [[1,1,1],[1,2,3]]
y = [3,1]

3.普通线性回归

from sklearn.linear_model import LinearRegression

# 第0步
reg1 = LinearRegression()

# 第1步
reg1.fit(X,y)

reg1.predict(np.array([[2,2,2]]))

4.岭回归

from sklearn.linear_model import Ridge

# 第0步
reg2 = Ridge()
# 第1步
reg2.fit(X,y)
reg2.predict([[2,2,2]])

• 拓展

import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model

# X is the 10x10 Hilbert matrix
X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
y = np.ones(10)

###############################################################################
# Compute paths

n_alphas = 200
alphas = np.logspace(-10, -2, n_alphas)
clf = linear_model.Ridge(fit_intercept=False)

coefs = []
for a in alphas:
    clf.set_params(alpha=a)
    clf.fit(X, y)
    coefs.append(clf.coef_)

###############################################################################
# Display results
plt.figure(figsize=(12,9))
ax = plt.gca()


ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim()[::-1])  # reverse axis
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization')
plt.axis('tight')
plt.show()

拓展图.png

五.Lasso回归

least absolute shrinkage and selection operator，最小绝对值收缩和选择算子
与岭回归类似，它也是通过增加惩罚函数来判断、消除特征间的共线性。

岭回归1.png

当λ足够小时，一些影响较弱的系数会因此被迫缩减到0

• 优点

跟岭回归类似，不同的算法

实例 : 波士顿房价信息

1.导入

from sklearn.linear_model import Lasso
from sklearn.datasets import load_boston
boston=load_boston()

2.数据处理

X=boston.data[:-20]
Y=boston["target"][:-20]
X_test = boston.data[-20:]
Y_test = boston['target'][-20:]
names=boston["feature_names"]

3.使用lasso

lasso=Lasso(alpha=0.7)
lasso.fit(X,Y)
display(lasso.predict(X_test),Y_test)

六.普通线性回归、岭回归、Lasso回归比较

通过案例来进行比较

1.导入模块

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# 根据实际值与预测值，给模型打分
from sklearn.metrics import r2_score 

2.准备数据

np.random.seed(42) #给numpy随机数指定种子，这样生成随机数，就会固定

n_samples,n_features = 50,200

#生成样本
x = np.random.randn(n_samples,n_features)

#系数，也就是W
coef = 3*np.random.randn(n_features)

#系数归零化索引
inds = np.arange(n_features)

#打乱顺序
np.random.shuffle(inds)

#对系数进行归零化处理
coef[inds[10:]] = 0

#目标值
y = np.dot(x,coef)

#增加噪声
y += 0.01*np.random.normal(n_samples)

3.训练数据/测试数据

# 训练数据
x_train,y_train = x[:n_samples//2],y[:n_samples//2]
#测试数据
x_test,y_test = x[n_samples//2:],y[n_samples//2:]

4.普通线性回归

#使用普通线性回归
from sklearn.linear_model import LinearRegression
lreg = LinearRegression()

#训练数据
lreg.fit(x_train,y_train)

#预测数据
y_pred = lreg.predict(x_test)
r2_score(y_test,y_pred)

5.岭回归

#使用岭回归
from sklearn.linear_model import Ridge
ridge = Ridge()

#训练数据
ridge.fit(x_train,y_train)

#预测数据
y_pred = ridge.predict(x_test)

#获取回归模型的分数
r2_score(y_test,y_pred)

6.Lasso

from sklearn.linear_model import Lasso

lasso = Lasso()

lasso.fit(x_train,y_train)

y_pred_lasso = lasso.predict(x_test)

r2_score(y_test,y_pred_lasso)

7.绘制图标展示数据

# 画出参数
plt.figure(figsize=(12,8))

plt.subplot(221)
plt.plot(reg.coef_,color = 'lightgreen',lw = 2,label = 'lr coefficients')
plt.legend()

plt.subplot(222)
plt.plot(reg2.coef_,color = 'red',lw = 2,label = 'ridge coefficients')
plt.legend()

plt.subplot(223)
plt.plot(reg3.coef_,color = 'gold',lw = 2,label = 'lasso coefficients')
plt.legend()

plt.subplot(224)
plt.plot(coef,color = 'navy',lw = 2,label = 'original coefficients')
plt.legend()

回归比较.png

七.logistics

• 什么是逻辑斯蒂函数

  
  
  

  逻辑斯蒂图1.png
  
  
  

  逻辑斯蒂图2.png
  
  

  根据现有数据对分类边界线建立回归公式，依此进行分类

• 逻辑斯蒂回归---->分类

利用Logistics回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式，以此进行分类。这里的“回归” 一词源于最佳拟合，表示要找到最佳拟合参数集

Logistic Regression和Linear Regression的原理是相似的，可以简单的描述为这样的过程

（1）找一个合适的预测函数，一般表示为h函数，该函数就是我们需要找的分类函数，它用来预测输入数据的判断结果。这个过程是非常关键的，需要对数据有一定的了解或分析，知道或者猜测预测函数的“大概”形式，比如是线性函数还是非线性函数
（2）构造一个Cost函数（损失函数），该函数表示预测的输出（h）与训练数据类别（y）之间的偏差，可以是二者之间的差（h-y）或者是其他的形式。综合考虑所有训练数据的“损失”，将Cost求和或者求平均，记为J(θ)函数，表示所有训练数据预测值与实际类别的偏差
（3）显然，J(θ)函数的值越小表示预测函数越准确（即h函数越准确），所以这一步需要做的是找到J(θ)函数的最小值。找函数的最小值有不同的方法，Logistic Regression实现时有梯度下降法（Gradient Descent）

• 站在巨人的肩膀上

  
  
  

  图1.png
  
  
  

  图2.png
  
  
  

  图3.png
  
  
  

  图4.png
  
  

  举个例子

假如有一个罐子，里面有黑白两种颜色的球，数目多少不知，两种颜色的比例也不知。我 们想知道罐中白球和黑球的比例，但我们不能把罐中的球全部拿出来数。现在我们可以每次任意从已经摇匀的罐中拿一个球出来，记录球的颜色，然后把拿出来的球 再放回罐中。这个过程可以重复，我们可以用记录的球的颜色来估计罐中黑白球的比例。假如在前面的一百次重复记录中，有七十次是白球，请问罐中白球所占的比例最有可能是多少？很多人马上就有答案了：70%。而其后的理论支撑是什么呢？

    我们假设罐中白球的比例是p，那么黑球的比例就是1-p。因为每抽一个球出来，在记录颜色之后，我们把抽出的球放回了罐中并摇匀，所以每次抽出来的球的颜 色服从同一独立分布。这里我们把一次抽出来球的颜色称为一次抽样。题目中在一百次抽样中，七十次是白球的概率是P(Data | M)，这里Data是所有的数据，M是所给出的模型，表示每次抽出来的球是白色的概率为p。如果第一抽样的结果记为x1，第二抽样的结果记为x2... 那么Data = (x1,x2,…,x100)。这样，

　　　　P(Data | M)

　　　　　= P(x1,x2,…,x100|M)

　　　　　= P(x1|M)P(x2|M)…P(x100|M)

　　　　　= p^70(1-p)^30.

那么p在取什么值的时候，P(Data |M)的值最大呢？将p^70(1-p)^30对p求导，并其等于零。

　　　　70p^69(1-p)^30-p^70*30(1-p)^29=0。

　　　　解方程可以得到p=0.7。

在边界点p=0,1，P(Data|M)=0。所以当p=0.7时，P(Data|M)的值最大。这和我们常识中按抽样中的比例来计算的结果是一样的。

• 优缺点

实现简单，易于理解和实现；计算代价不高，速度很快，存储资源低
容易欠拟合，分类精度可能不高

实战

• 手写数字数据集的分类
  1.导入

from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression

2.处理数据

digits = datasets.load_digits()
x_digits = digits.data
y_digits = digits.target

x_train = x_digits[:round(.9*len(x_digits))]
x_test = x_digits[round(.9*len(x_digits)):]

y_train = y_digits[:round(.9*len(y_digits))]
y_test = y_digits[round(.9*len(y_digits)):]

3.训练和预测

knn = KNeighborsClassifier()
logistic = LogisticRegression()

display('KNN score: %f'%knn.fit(x_train,y_train).score(x_test,y_test),
       'Logistic Score: %f'%logistic.fit(x_train,y_train).score(x_test,y_test))

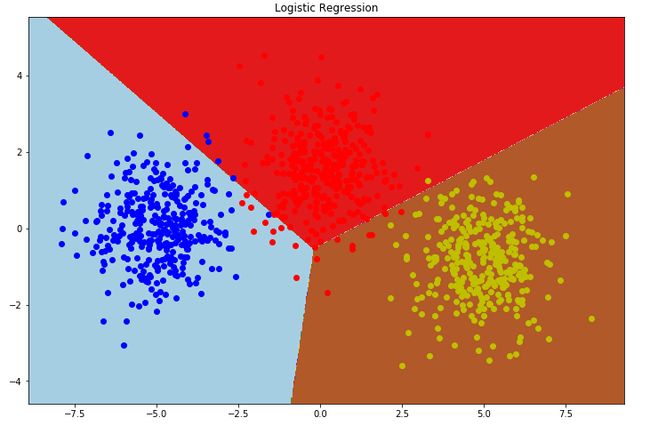
• 使用make_blobs产生数据集进行分类
  1.导入

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

from sklearn.datasets import make_blobs #生成用于聚类的各向同性高斯斑点
from sklearn.linear_model import LogisticRegression

2.处理数据

# 设置三个中心点，建立一个三分类问题
centers = [[-5,0],[0,1.5],[5,-1]]
X,y = make_blobs(n_samples=1000, centers=centers, random_state=40)

3.训练数据

# 第1步：训练
clf = LogisticRegression()
clf.fit(X,y)

4.图片背景图片点

# 背景（网格）
h = 0.02
x_min,x_max = X[:,0].min()-1,X[:,0].max()+1
y_min,y_max = X[:,1].min()-1,X[:,1].max()+1

# 从坐标向量返回坐标矩阵
# 图片的背景显示坐标
xx,yy = np.meshgrid(np.arange(x_min,x_max,h),
                   np.arange(y_min,y_max,h))

5.预测数据

# 得到网格上每个点的分类情况
Z = clf.predict(np.c_[xx.ravel(),yy.ravel()])
z = Z.reshape(xx.shape)
#预测背景图片的点，从而知道划分区域

6.画图

# 画图
plt.figure()
#绘制轮廓线，填充轮廓
#plt.contourf(xx,yy,z,cmap = plt.cm.Paired)
plt.pcolormesh(xx,yy,z,cmap = plt.cm.Paired)
plt.title("Logistic Regression")
plt.axis('tight')

colors = 'bry'
for i,color in zip(clf.classes_,colors):
    idx = np.where(y==i)
    plt.scatter(X[idx,0],X[idx,1],c=color,cmap = plt.cm.Paired)

分类图.png

八.人脸自动补全

1.导包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.neighbors import KNeighborsRegressor
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_olivetti_faces

2.提取数据

#加载人脸数据
faces = fetch_olivetti_faces()
#生成训练数据和预测数据
data = faces.data
target = faces.target
# 上半部分脸是训练数据,下半部分脸是预测数据.
face_up = data[:,:2048] # 训练数据
face_down = data[:,2048:] # 标记
# 拆分数据,留一些做预测数据
X_train,X_test, y_train,y_test = train_test_split(face_up, face_down, test_size=0.1)

3.训练模型

#创建机器学习模型，以字典的形式包含四种模型
estimators = {
    'knn': KNeighborsRegressor(),
    'linear': LinearRegression(),
    'ridge': Ridge(),
    'extratree': ExtraTreesRegressor()
}

4.训练数据并预测数据

y_pred = {}
for key,estimator in estimators.items():
    # 训练
    estimator.fit(X_train,y_train)
    # 预测
    y_ = estimator.predict(X_test)
    y_pred[key] = y_
    

5.绘制人脸预测图像

#绘制预测的人脸
# 展示结果.
# 8行6列
plt.figure(figsize=(8* 3,6* 3.5))
for i in range(8):
    axes = plt.subplot(8,6, i * 6 + 1)
    # 拼出完整的脸
    face_up = X_test[i*5].reshape(32,64)
    face_down = y_test[i*5].reshape(32,64)
    face = np.vstack((face_up,face_down))
    axes.imshow(face, cmap='gray')
    # 去掉轴
    axes.axis('off')
    # 加个标题
    if i == 0:
        axes.set_title('True', fontdict=dict(fontsize=20))
        
    # 第二列显示真实的上半部分脸
    axes = plt.subplot(8,6, i*6 + 2)
    axes.imshow(face_up, cmap='gray')
    axes.axis('off')
    if i == 0:
        axes.set_title('half face', fontdict=dict(fontsize=20))
        
    # 循环的画出后面四列
    for j,key in enumerate(y_pred):
        axes = plt.subplot(8,6, i*6 + 3 + j)
        # 拼出真实上半部分脸和下半部分脸的结合
        face_down_pred = y_pred[key][i*5].reshape(32,64)
        face_pred = np.vstack((face_up, face_down_pred))
        axes.imshow(face_pred, cmap='gray')
        if i == 0 :
            axes.set_title(key, fontdict=dict(fontsize=20))
        axes.axis('off')

效果图

人脸识别.png