递归实现迷宫、八皇后、汉罗塔 等问题
断了两天、所以还是开心学算法的第七天
程序调用自身的编程技巧称为递归( recursion)。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说,递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时,递归前进;当边界条件满足时,递归返回。
递归简言之就是自己调用自己,每一次传入的参数都不同,并且需要设置一个边界条件使其回溯,递归在调用的时候会开辟一个递归栈,当没有边界条件的时候就会发生栈溢出。
使用递归需要知道:
- 执行一个方法时就会创建一个新的受保护的独立空间也就是栈空间。
- 方法的局部变量是独立的,不会相互影响。
- 递归必须向退出条件逼近,否则就会无限的递归最终发生栈溢出。
- 当一个方法执行完毕,或者遇到return时,就会返回,遵守谁调用,就将结果返回给谁,同时方法
执行完毕或者返回时,该方法也就执行完毕。
求1~n的阶乘
实现思路:
这里可以边界条件就是n == 1时开始回溯,当传入n时首先判断n是否等于1如果等于1直接的返回不等于执行第二个return语句,传入的参数向n = 1开始逼近,当return factorial(n) OR return factorial(n+1)这样就会发生无限的递归。当 n = 5时第一次factorial(4)*5;调用当前函数,会出现factorial(3)*4,直至等于1时回溯,1 * 2依次类推就可以求解。
代码如下:
//递归求n的阶乘
public static int factorial(int n){
if (n == 1){
return 1;
}
return factorial(n-1)*n;
}
迷宫问题
问题描述:用一个二维数组模拟一个迷宫的地图,当为0的时候表示路径可走,当为1的时候表示此路不同,在这种情况下找到一个正确的路径。
列如:
最终打印出的结果:
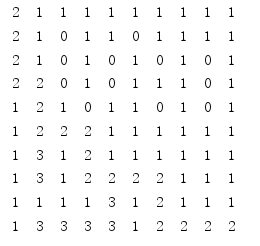
这里需要解释一下:2表示的是正确的路径,当然路径不知这一条,3表示的当走到这一点发现不能继续向四周找,所以需要设置当前的路不能走,防止死循环出现。这里可以简单的理解一条路走到黑,走不了就回溯。
代码如下:
//打印迷宫
public static void printfMap(int[][] map){
for (int i = 0; i < map.length; i++) {
for (int j = 0; j < map[0].length; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}
}
//map表示的是地图,ij表示的是从那个位置开始
//思路描述:0表示可走,1表示不可走,2表示正确的迷宫途径,3表示走过的但是走不通
//寻找路径
public static boolean findPath(int[][] map,int i,int j){
if (map[map.length-1][map[0].length-1] == 2){
//表示走到最后哪一个点
return true;
}else{
//防止下标越界
if (i < map.length && j < map[0].length && i >= 0 && j >= 0){
//方向寻找的方向 下,右,上,左
if (map[i][j] == 0){
//表示当前的点没有走过
map[i][j] = 2;
if (findPath(map,i+1,j)){
//向下
return true;
}else if (findPath(map,i,j+1)){
//向右
return true;
}else if (findPath(map,i-1,j)){
//向上
return true;
}else if (findPath(map,i,j-1)){
//向左
return true;
}else{
//表示当前点走不通
map[i][j] = 3;
return false;
}
}else{
return false;
}
}else {
return false;
}
}
}
}
汉罗塔
汉诺塔(Tower of Hanoi),又称河内塔,是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
问题描述:
存在三个柱子,初始的情况下A上面有N个盘子,需要将A上的N个盘子借助B移动到C上,需要注意的是,三根柱子上面的所有盘子大的在最下面,这规律在三个柱子上是不能改变的。
举一个n=3的列子:
第1移动:1: A----->C
第2移动:2: A----->B
第3移动:1: C----->B
第4移动:3: A----->C
第5移动:1: B----->A
第6移动:2: B----->C
第7移动:1: A----->C
以上是移动那个盘子及详细的移动过程。
//记录移动的次数
private static int count = 1;
//打印移动轨迹的函数
private static void move(int disks,char N,char M){
System.out.println("第"+count+++"移动:"+disks+": "+N+"----->"+M);
}
//递归实现汉罗塔的函数
private static void hanoi(int n,char A,char B,char C){
//边界条件
if (n == 1){
move(1,A,C);
return;
}
hanoi(n-1,A,C,B);//把n-1的圆盘记住C移动到B上
move(n,A,C);//将第n个盘子移动到了C上
hanoi(n-1,B,A,C);//借助A盘将B中1~n-1个盘子移动到C
}
八皇后问题
问题描述:八皇后每个皇后不能出现在同一行,同一列,同一对角线,因为这样的话会出现互相攻击。
思路阐述:array[i] == array[n] || Math.abs(n-i) == Math.abs(array[n] - array[i]这个条件的话就是用来判断是否在同一列和同一对角线上。这里不需要判断是否同一行的原因是传入的n就是表示的行数。使用一维数组来缓存皇后所处的位置数组的下标+1表示的是行数,val+1表示的是列数。这里说一下位置是如何查找的,初始从第一行开始找,依次第一列,递归调用,然后使用for循环来看皇后所可以处的位置,每当存放一个就会判断依次,如果成功直接递归调用,否则直到for循环结束回溯,或者到n == max时回溯。直到当 n = 0,i = 8时表示执行结束。
//定义存在多少个皇后
private int max = 8;
//定义一个数组保存皇后放置的位置结果,arr = {0,4,7,5,2,6,1,3}
private int[] array = new int[max];
//统计一共有多少中解法
private static int count = 0;
//将皇后的位置输出
private void print(){
count++;
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]+" ");
}
System.out.println();
}
//查看当我们放置第n个皇后,就去检测该皇后是否和前面已经摆放的皇后冲突
private boolean judge(int n){
for (int i = 0; i < n; i++) {
//第一个条件判断的是表示当前是否在同一列,第二个条件判断是否在同一斜线
if (array[i] == array[n] || Math.abs(n-i) == Math.abs(array[n] - array[i])){
return false;
}
}
return true;
}
//编写方法,放置第n个皇后
private void check(int n){
if (n == max){
//表示的皇后的位置已经占满
print();
return;
}
//依次放入皇后,并判断是否冲突
for(int i = 0;i < max;i++){
//先把当前这个皇后n放到该行的第1列
array[n] = i;
//判断放置当前位置时是否冲突
if (judge(n)){
//表示不冲突接着放n+1皇后
check(n + 1);
}
}
}

