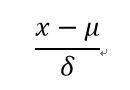数据的标准化(normalization)和归一化
数据的标准化(normalization)
- 将数据按比例缩放,使之落入一个小的特定区间
- 去除数据的单位限制,将其转化为无量纲的纯数值
数据标准化方法
- 直线型方法(如极值法、标准差法)
- 折线型方法(如三折线法)
- 曲线型方法(如半正态性分布)
其中最典型的是归一化,即将数据映射到 (0,1)区间
也就是说,归一化是特殊的标准化
归一化的目标
1 把数变为(0,1)之间的小数
主要是为了数据处理方便提出来的,把数据映射到0~1范围之内处理,更加便捷快速,应该归到数字信号处理范畴之内。
2 把有量纲表达式变为无量纲表达式
归一化是一种简化计算的方式,即将有量纲的表达式,经过变换,化为无量纲的表达式,成为纯量。 比如,复数阻抗可以归一化书写:Z = R + jωL = R(1 + jωL/R) ,复数部分变成了纯数量了,没有量纲。
另外,微波之中也就是电路分析、信号系统、电磁波传输等,有很多运算都可以如此处理,既保证了运算的便捷,又能凸现出物理量的本质含义。
归一化后有两个好处
1. 提升模型的收敛速度
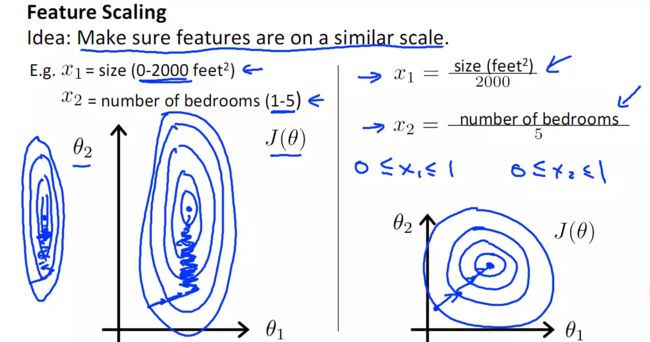
如下图,x1的取值为0-2000,而x2的取值为1-5,假如只有这两个特征,对其进行优化时,会得到一个窄长的椭圆形,导致在梯度下降时,梯度的方向为垂直等高线的方向而走之字形路线,这样会使迭代很慢,相比之下,右图的迭代就会很快(理解:也就是步长走多走少方向总是对的,不会走偏)
2.提升模型的精度
归一化的另一好处是提高精度,这在涉及到一些距离计算的算法时效果显著,比如算法要计算欧氏距离,上图中x2的取值范围比较小,涉及到距离计算时其对结果的影响远比x1带来的小,所以这就会造成精度的损失。所以归一化很有必要,他可以让各个特征对结果做出的贡献相同。
在多指标评价体系中,由于各评价指标的性质不同,通常具有不同的量纲和数量级。当各指标间的水平相差很大时,如果直接用原始指标值进行分析,就会突出数值较高的指标在综合分析中的作用,相对削弱数值水平较低指标的作用。因此,为了保证结果的可靠性,需要对原始指标数据进行标准化处理。
在数据分析之前,我们通常需要先将数据标准化(normalization),利用标准化后的数据进行数据分析。数据标准化也就是统计数据的指数化。数据标准化处理主要包括数据同趋化处理和无量纲化处理两个方面。数据同趋化处理主要解决不同性质数据问题,对不同性质指标直接加总不能正确反映不同作用力的综合结果,须先考虑改变逆指标数据性质,使所有指标对测评方案的作用力同趋化,再加总才能得出正确结果。数据无量纲化处理主要解决数据的可比性。经过上述标准化处理,原始数据均转换为无量纲化指标测评值,即各指标值都处于同一个数量级别上,可以进行综合测评分析。
从经验上说,归一化是让不同维度之间的特征在数值上有一定比较性,可以大大提高分类器的准确性。
- 深度学习中数据归一化可以防止模型梯度爆炸。(这个好像不是很懂)
数据需要归一化的机器学习算法
需要归一化的模型:
有些模型在各个维度进行不均匀伸缩后,最优解与原来不等价,例如SVM(距离分界面远的也拉近了,支持向量变多?)。对于这样的模型,除非本来各维数据的分布范围就比较接近,否则必须进行标准化,以免模型参数被分布范围较大或较小的数据dominate。(Seurat分析等单细胞数据分析常用的SVM)
有些模型在各个维度进行不均匀伸缩后,最优解与原来等价,例如logistic regression(因为θ的大小本来就自学习出不同的feature的重要性吧?)。对于这样的模型,是否标准化理论上不会改变最优解。但是,由于实际求解往往使用迭代算法,如果目标函数的形状太“扁”,迭代算法可能收敛得很慢甚至不收敛(模型结果不精确)。所以对于具有伸缩不变性的模型,最好也进行数据标准化。
有些模型/优化方法的效果会强烈地依赖于特征是否归一化,如LogisticReg,SVM,NeuralNetwork,SGD等。
不需要归一化的模型:
(0/1取值的特征通常不需要归一化,归一化会破坏它的稀疏性。)
有些模型则不受归一化影响,如DecisionTree。
ICA好像不需要归一化(因为独立成分如果归一化了就不独立了?)。
基于平方损失的最小二乘法OLS不需要归一化。
提一个问题
什么时候用归一化?什么时候用标准化?
(1)如果对输出结果范围有要求,用归一化。
(2)如果数据较为稳定,不存在极端的最大最小值,用归一化。
(3)如果数据存在异常值和较多噪音,用标准化,可以间接通过中心化避免异常值和极端值的影响。
需要进行归一化/标准化的模型
(1)SVM
不同的模型对特征的分布假设是不一样的。比如SVM 用高斯核的时候,所有维度共用一个方差,这不就假设特征分布是圆的么,输入椭圆的就坑了人家,所以简单的归一化都还不够好,来杯白化才有劲。比如用树的时候就是各个维度各算各的切分点,没所谓。
(2)KNN
需要度量距离的模型,一般在特征值差距较大时,都会进行归一化/标准化。不然会出现“大数吃小数”。
(3)神经网络
1)数值问题
归一化/标准化可以避免一些不必要的数值问题。输入变量的数量级未致于会引起数值问题吧,但其实要引起也并不是那么困难。因为tansig(tanh)的非线性区间大约在[-1.7,1.7]。意味着要使神经元有效,tansig( w1x1 + w2x2 +b) 里的 w1x1 +w2x2 +b 数量级应该在 1 (1.7所在的数量级)左右。这时输入较大,就意味着权值必须较小,一个较大,一个较小,两者相乘,就引起数值问题了。
假如你的输入是421,你也许认为,这并不是一个太大的数,但因为有效权值大概会在1/421左右,例如0.00243,那么,在matlab里输入 421·0.00243 == 0.421·2.43,会发现不相等,这就是一个数值问题
PCA算法
常见的数据归一化方法
最常用的是 min-max标准化 和 z-score 标准化。
min-max标准化(Min-max normalization)/0-1标准化(0-1 normalization)/线性函数归一化/离差标准化
是对原始数据的线性变换,使结果落到[0,1]区间,转换函数如下:
其中max为样本数据的最大值,min为样本数据的最小值。
def Normalization(x):
return [(float(i)-min(x))/float(max(x)-min(x)) for i in x]
如果想要将数据映射到[-1,1],则将公式换成:
x* = x* * 2 -1
或者进行一个近似
x* = (x - x_mean)/(x_max - x_min), x_mean表示数据的均值。
def Normalization2(x):
return [(float(i)-np.mean(x))/(max(x)-min(x)) for i in x]
这种方法有一个缺陷就是当有新数据加入时,可能导致max和min的变化,需要重新定义。
将数据归一化到[a,b]区间范围的方法:
(1)首先找到原本样本数据X的最小值Min及最大值Max
(2)计算系数:k=(b-a)/(Max-Min)
(3)得到归一化到[a,b]区间的数据:Y=a+k(X-Min) 或者 Y=b+k(X-Max)
即一个线性变换,在坐标上就是求直线方程,先求出系数,代入一个点对应的值(x的最大/最小就对应y的最大/最小)就ok了。
z-score 标准化(zero-mean normalization)
最常见的标准化方法就是Z标准化,也是SPSS中最为常用的标准化方法,spss默认的标准化方法就是z-score标准化。
也叫标准差标准化,这种方法给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。
经过处理的数据符合标准正态分布,即均值为0,标准差为1,注意,一般来说z-score不是归一化,而是标准化,归一化只是标准化的一种。
其转化函数为:
x* = (x - μ ) / σ
其中μ为所有样本数据的均值,σ为所有样本数据的标准差。
z-score标准化方法适用于属性A的最大值和最小值未知的情况,或有超出取值范围的离群数据的情况。该种标准化方式要求原始数据的分布可以近似为高斯分布,否则效果会变得很糟糕。
标准化的公式很简单,步骤如下
1.求出各变量(指标)的算术平均值(数学期望)xi和标准差si ;
2.进行标准化处理:
zij=(xij-xi)/si
其中:zij为标准化后的变量值;xij为实际变量值。
3.将逆指标前的正负号对调。
标准化后的变量值围绕0上下波动,大于0说明高于平均水平,小于0说明低于平均水平。
def z_score(x, axis):
x = np.array(x).astype(float)
xr = np.rollaxis(x, axis=axis)
xr -= np.mean(x, axis=axis)
xr /= np.std(x, axis=axis)
# print(x)
return x
为什么z-score 标准化后的数据标准差为1?
x-μ只改变均值,标准差不变,所以均值变为0
(x-μ)/σ只会使标准差除以σ倍,所以标准差变为1
这两种最常用方法使用场景:
1、在分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候,第二种方法(Z-score standardization)表现更好。
2、在不涉及距离度量、协方差计算、数据不符合正态分布的时候,可以使用第一种方法或其他归一化方法。比如图像处理中,将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。
原因是使用第一种方法(线性变换后),其协方差产生了倍数值的缩放,因此这种方式无法消除量纲对方差、协方差的影响,对PCA分析影响巨大;同时,由于量纲的存在,使用不同的量纲、距离的计算结果会不同。而在第二种归一化方式中,新的数据由于对方差进行了归一化,这时候每个维度的量纲其实已经等价了,每个维度都服从均值为0、方差1的正态分布,在计算距离的时候,每个维度都是去量纲化的,避免了不同量纲的选取对距离计算产生的巨大影响。
log函数转换
通过以10为底的log函数转换的方法同样可以实现归一下,具体方法如下:
看了下网上很多介绍都是x*=log10(x),其实是有问题的,这个结果并非一定落到[0,1]区间上,应该还要除以log10(max),max为样本数据最大值,并且所有的数据都要大于等于1。
atan函数转换
用反正切函数也可以实现数据的归一化。
使用这个方法需要注意的是如果想映射的区间为[0,1],则数据都应该大于等于0,小于0的数据将被映射到[-1,0]区间上,而并非所有数据标准化的结果都映射到[0,1]区间上。
Decimal scaling小数定标标准化
这种方法通过移动数据的小数点位置来进行标准化。小数点移动多少位取决于属性A的取值中的最大绝对值。
将属性A的原始值x使用decimal scaling标准化到x'的计算方法是:
x'=x/(10^j)
其中,j是满足条件的最小整数。
例如 假定A的值由-986到917,A的最大绝对值为986,为使用小数定标标准化,我们用每个值除以1000(即,j=3),这样,-986被规范化为-0.986。
注意,标准化会对原始数据做出改变,因此需要保存所使用的标准化方法的参数,以便对后续的数据进行统一的标准化。
Logistic/Softmax变换
模糊量化模式
新数据=1/2+1/2sin[派3.1415/(极大值-极小值)*(X-(极大值-极小值)/2) ] X为原数据
其中我们最生物信息学的最关心的还是z-score的标准化的方法(单细胞数据主要还是需要PCA降维)
这里我们详细说一下这个算法
Z-Score标准化是数据处理的一种常用方法。通过它能够将不同量级的数据转化为统一量度的Z-Score分值进行比较。
一句话解释版本:
Z-Score通过(x-μ)/σ将两组或多组数据转化为无单位的Z-Score分值,使得数据标准统一化,提高了数据可比性,削弱了数据解释性。
数据分析与挖掘体系位置
Z-Score标准化是数据处理的方法之一。在数据标准化中,常见的方法有如下三种:
Z-Score 标准化
最大最小标准化
小数定标法
本篇主要介绍第一种数据标准化的方法,Z-Score标准化。
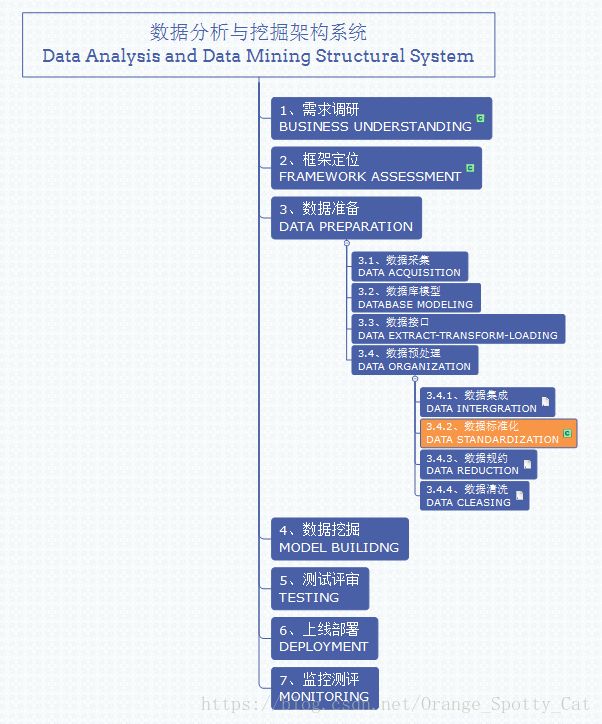
此方法在整个数据分析与挖掘体系中的位置如下图所示。
Z-Score的定义
Z-Score处理方法处于整个框架中的数据准备阶段。也就是说,在源数据通过网络爬虫、接口或其他方式进入数据库中后,下一步就要进行的数据预处理阶段中的重要步骤。
数据分析与挖掘中,很多方法需要样本符合一定的标准,如果需要分析的诸多自变量不是同一个量级,就会给分析工作造成困难,甚至影响后期建模的精准度。
举例来说,假设我们要比较A与B的考试成绩,A的考卷满分是100分(及格60分),B的考卷满分是700分(及格420分)。很显然,A考出的70分与B考出的70分代表着完全不同的意义。但是从数值来讲,A与B在数据表中都是用数字70代表各自的成绩。
那么如何能够用一个同等的标准来比较A与B的成绩呢?Z-Score就可以解决这一问题。
下图描述了Z-Score的定义以及各种特征。
Z-Score的目的
如上图所示,Z-Score的主要目的就是将不同量级的数据统一转化为同一个量级,统一用计算出的Z-Score值衡量,以保证数据之间的可比性。
Z-Score的理解与计算
在对数据进行Z-Score标准化之前,我们需要得到如下信息:
1)总体数据的均值(μ)
在上面的例子中,总体可以是整个班级的平均分,也可以是全市、全国的平均分。
2)总体数据的标准差(σ)
这个总体要与1)中的总体在同一个量级。
3)个体的观测值(x)
在上面的例子中,即A与B各自的成绩。
通过将以上三个值代入Z-Score的公式,即:
我们就能够将不同的数据转换到相同的量级上,实现标准化。
重新回到前面的例子,假设:A班级的平均分是80,标准差是10,A考了90分;B班的平均分是400,标准差是100,B考了600分。
通过上面的公式,我们可以计算得出,A的Z-Score是1((90-80)/10),B的Z-Socre是2((600-400)/100)。因此B的成绩更为优异。
反之,若A考了60分,B考了300分,A的Z-Score是-2,B的Z-Score是-1。因此A的成绩更差。
因此,可以看出来,通过Z-Score可以有效的把数据转换为统一的标准,但是需要注意,并进行比较。Z-Score本身没有实际意义,它的现实意义需要在比较中得以实现,这也是Z-Score的缺点之一。
Z-Score的优缺点
Z-Score最大的优点就是简单,容易计算,在R中,不需要加载包,仅仅凭借最简单的数学公式就能够计算出Z-Score并进行比较。此外,Z-Score能够应用于数值型的数据,并且不受数据量级的影响,因为它本身的作用就是消除量级给分析带来的不便。
但是Z-Score应用也有风险。首先,估算Z-Score需要总体的平均值与方差,但是这一值在真实的分析与挖掘中很难得到,大多数情况下是用样本的均值与标准差替代。其次,Z-Score对于数据的分布有一定的要求,正态分布是最有利于Z-Score计算的。最后,Z-Score消除了数据具有的实际意义,A的Z-Score与B的Z-Score与他们各自的分数不再有关系,因此Z-Score的结果只能用于比较数据间的结果,数据的真实意义还需要还原原值。