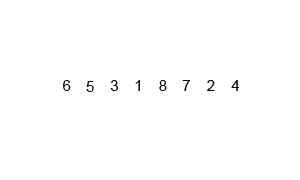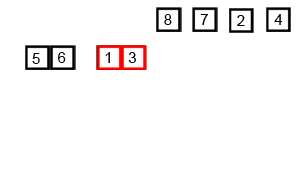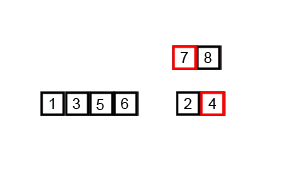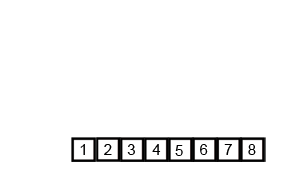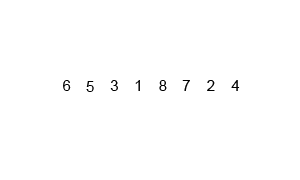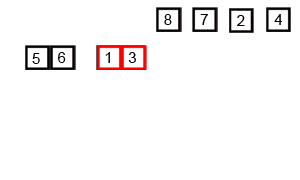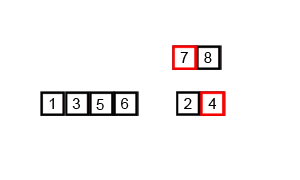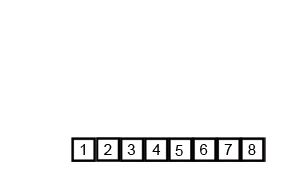算法-排序算法:归并排序(Merge Sort)【O(nlogn)】【自顶向下:递归方式;自底向上:非递归方式】
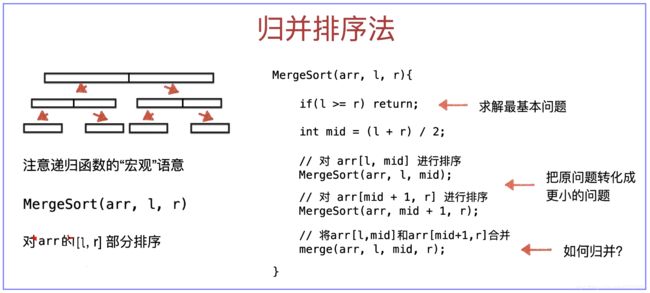
归并排序(Merge Sort):建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
一、归并排序-算法描述:
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列;
- 归并的过程无法原地完成;
二、归并排序-过程分析
每2组合并为1组时,都是将这2组中的所有数按照从小到大进行排序
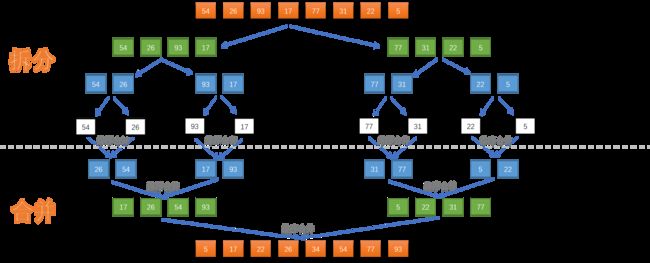
三、归并排序-动图演示
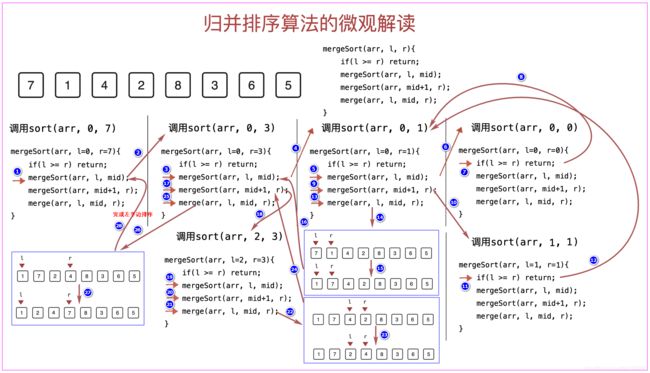
四、归并排序的微观解读
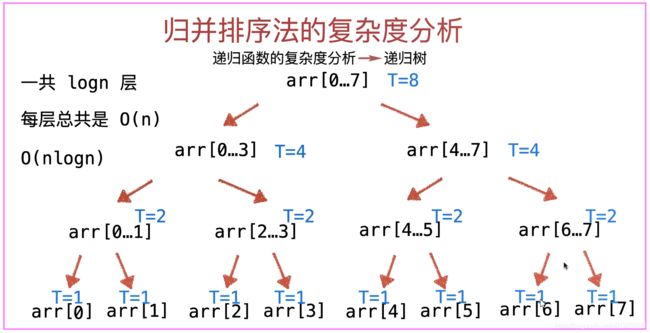
五、归并排序的复杂度分析
六、归并排序(自顶向下)-代码实现
1、归并排序-原始版
import java.util.Arrays;
public class MergeSort {
// 自顶向下的归并排序
private static void sort(int[] arr, int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
System.out.println("left = " + left + "; right = " + right + "; mid = " + mid + "; arr = " + Arrays.toString(arr));
sort(arr, left, mid);//左边归并排序,使得左子序列有序
sort(arr, mid + 1, right);//右边归并排序,使得右子序列有序
merge(arr, left, mid, right);//将两个有序子数组合并操作
System.out.println("arr = " + Arrays.toString(arr) + "\n");
}
}
private static void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[arr.length]; //建一个长度等于原数组长度的临时数组
int i = left;//左序列指针
int j = mid + 1;//右序列指针
int t = 0;//临时数组指针
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[t++] = arr[i++];
} else {
temp[t++] = arr[j++];
}
}
while (i <= mid) {
//将左边剩余元素填充进temp中
temp[t++] = arr[i++];
}
while (j <= right) {
//将右序列剩余元素填充进temp中
temp[t++] = arr[j++];
}
t = 0;
//将temp中的元素全部拷贝到原数组中
while (left <= right) {
arr[left++] = temp[t++];
}
}
public static void main(String[] args) {
int[] arr = {
7, 1, 4, 2, 8, 3, 6, 5};
MergeSort.sort(arr, 0, arr.length - 1);
System.out.println("Arrays.toString(arr) = " + Arrays.toString(arr));
}
}
输出结果:
left = 0; right = 7; mid = 3; arr = [7, 1, 4, 2, 8, 3, 6, 5]
left = 0; right = 3; mid = 1; arr = [7, 1, 4, 2, 8, 3, 6, 5]
left = 0; right = 1; mid = 0; arr = [7, 1, 4, 2, 8, 3, 6, 5]
arr = [1, 7, 4, 2, 8, 3, 6, 5]
left = 2; right = 3; mid = 2; arr = [1, 7, 4, 2, 8, 3, 6, 5]
arr = [1, 7, 2, 4, 8, 3, 6, 5]
arr = [1, 2, 4, 7, 8, 3, 6, 5]
left = 4; right = 7; mid = 5; arr = [1, 2, 4, 7, 8, 3, 6, 5]
left = 4; right = 5; mid = 4; arr = [1, 2, 4, 7, 8, 3, 6, 5]
arr = [1, 2, 4, 7, 3, 8, 6, 5]
left = 6; right = 7; mid = 6; arr = [1, 2, 4, 7, 3, 8, 6, 5]
arr = [1, 2, 4, 7, 3, 8, 5, 6]
arr = [1, 2, 4, 7, 3, 5, 6, 8]
arr = [1, 2, 3, 4, 5, 6, 7, 8]
Arrays.toString(arr) = [1, 2, 3, 4, 5, 6, 7, 8]
Process finished with exit code 0
2、归并排序-优化01(判断是否需要merge):
import java.util.Arrays;
public class MergeSort02 {
// 自顶向下的归并排序
private static void sort(int[] arr, int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
System.out.println("left = " + left + "; right = " + right + "; mid = " + mid + "; arr = " + Arrays.toString(arr));
sort(arr, left, mid);//左边归并排序,使得左子序列有序
sort(arr, mid + 1, right);//右边归并排序,使得右子序列有序
// 优化:如果左边序列的最大值小于右边序列的最小值,则不需要再merge操作,否则进行merge操作
if (arr[mid] > arr[mid + 1]) {
merge(arr, left, mid, right);//将两个有序子数组合并操作
}
System.out.println("arr = " + Arrays.toString(arr) + "\n");
}
}
// 合并两个有序的区间 arr[left, mid] 和 arr[mid + 1, right], 形成一个大的有序数组
private static void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[arr.length]; //建一个长度等于原数组长度的临时数组
int i = left;//左序列指针
int j = mid + 1;//右序列指针
int t = 0;//临时数组指针
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[t++] = arr[i++];
} else {
temp[t++] = arr[j++];
}
}
while (i <= mid) {
//将左边剩余元素填充进temp中
temp[t++] = arr[i++];
}
while (j <= right) {
//将右序列剩余元素填充进temp中
temp[t++] = arr[j++];
}
t = 0;
//将temp中的元素全部拷贝到原数组中
while (left <= right) {
arr[left++] = temp[t++];
}
}
public static void main(String[] args) {
int[] arr = {
7, 1, 4, 2, 8, 3, 6, 5};
MergeSort02.sort(arr, 0, arr.length - 1);
System.out.println("Arrays.toString(arr) = " + Arrays.toString(arr));
}
}
输出结果:
left = 0; right = 7; mid = 3; arr = [7, 1, 4, 2, 8, 3, 6, 5]
left = 0; right = 3; mid = 1; arr = [7, 1, 4, 2, 8, 3, 6, 5]
left = 0; right = 1; mid = 0; arr = [7, 1, 4, 2, 8, 3, 6, 5]
arr = [1, 7, 4, 2, 8, 3, 6, 5]
left = 2; right = 3; mid = 2; arr = [1, 7, 4, 2, 8, 3, 6, 5]
arr = [1, 7, 2, 4, 8, 3, 6, 5]
arr = [1, 2, 4, 7, 8, 3, 6, 5]
left = 4; right = 7; mid = 5; arr = [1, 2, 4, 7, 8, 3, 6, 5]
left = 4; right = 5; mid = 4; arr = [1, 2, 4, 7, 8, 3, 6, 5]
arr = [1, 2, 4, 7, 3, 8, 6, 5]
left = 6; right = 7; mid = 6; arr = [1, 2, 4, 7, 3, 8, 6, 5]
arr = [1, 2, 4, 7, 3, 8, 5, 6]
arr = [1, 2, 4, 7, 3, 5, 6, 8]
arr = [1, 2, 3, 4, 5, 6, 7, 8]
Arrays.toString(arr) = [1, 2, 3, 4, 5, 6, 7, 8]
Process finished with exit code 0
3、归并排序-优化02(对小规模数据使用插入排序):
当子序列的数据量小于设定数量后,使用插入排序方法代替归并排序,该优化方案不稳定,在一些脚本语言中(python、php、js)中可能性能更差。
import java.util.Arrays;
public class MergeSort03 {
// 自顶向下的归并排序
private static void sort(int[] arr, int left, int right) {
if (right - left > 2) {
int mid = left + (right - left) / 2;
System.out.println("left = " + left + "; right = " + right + "; mid = " + mid + "; arr = " + Arrays.toString(arr));
sort(arr, left, mid);//左边归并排序,使得左子序列有序
sort(arr, mid + 1, right);//右边归并排序,使得右子序列有序
// 优化:如果左边序列的最大值小于右边序列的最小值,则不需要再merge操作,否则进行merge操作
if (arr[mid] > arr[mid + 1]) {
merge(arr, left, mid, right);//将两个有序子数组合并操作
}
System.out.println("arr = " + Arrays.toString(arr) + "\n");
}else{
// 当数据量小于2时,使用插入排序【插入排序虽然时间复杂度为O(n^2),但是在小规模数据集上速度比归并排序快】
for (int i = left; i <= right; i++) {
//将arr[i]插入到已经排好序的arr[0,...,i)的合适的位置
int j;
int temp = arr[i];
for (j = i; j - 1 >= left && arr[j - 1] > temp; j--) {
// 循环继续条件:j - 1 >= 0 && arr[j - 1] > temp
arr[j] = arr[j - 1]; //将j-1位置的元素向后移动一位
}
arr[j] = temp;
}
}
}
// 合并两个有序的区间 arr[left, mid] 和 arr[mid + 1, right], 形成一个大的有序数组
private static void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[arr.length]; //建一个长度等于原数组长度的临时数组
int i = left;//左序列指针
int j = mid + 1;//右序列指针
int t = 0;//临时数组指针
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[t++] = arr[i++];
} else {
temp[t++] = arr[j++];
}
}
while (i <= mid) {
//将左边剩余元素填充进temp中
temp[t++] = arr[i++];
}
while (j <= right) {
//将右序列剩余元素填充进temp中
temp[t++] = arr[j++];
}
t = 0;
//将temp中的元素全部拷贝到原数组中
while (left <= right) {
arr[left++] = temp[t++];
}
}
public static void main(String[] args) {
int[] arr = {
7, 1, 4, 2, 8, 3, 6, 5};
MergeSort03.sort(arr, 0, arr.length - 1);
System.out.println("Arrays.toString(arr) = " + Arrays.toString(arr));
}
}
输出结果:
left = 0; right = 7; mid = 3; arr = [7, 1, 4, 2, 8, 3, 6, 5]
left = 0; right = 3; mid = 1; arr = [7, 1, 4, 2, 8, 3, 6, 5]
arr = [1, 2, 4, 7, 8, 3, 6, 5]
left = 4; right = 7; mid = 5; arr = [1, 2, 4, 7, 8, 3, 6, 5]
arr = [1, 2, 4, 7, 3, 5, 6, 8]
arr = [1, 2, 3, 4, 5, 6, 7, 8]
Arrays.toString(arr) = [1, 2, 3, 4, 5, 6, 7, 8]
Process finished with exit code 0
4、归并排序-优化03(只创建一个临时空间):
在排序前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间。也说明归并算法不是原地排序算法,需要临时空间。
import java.util.Arrays;
public class MergeSort04 {
// 自顶向下的归并排序
private static void sort(int[] arr, int left, int right, int[] temp) {
if (left < right) {
int mid = left + (right - left) / 2;
System.out.println("left = " + left + "; right = " + right + "; mid = " + mid + "; arr = " + Arrays.toString(arr));
sort(arr, left, mid, temp);//左边归并排序,使得左子序列有序
sort(arr, mid + 1, right, temp);//右边归并排序,使得右子序列有序
merge(arr, left, mid, right, temp);//将两个有序子数组合并操作
System.out.println("arr = " + Arrays.toString(arr) + "\n");
}
}
// 合并两个有序的区间 arr[left, mid] 和 arr[mid + 1, right], 形成一个大的有序数组
private static void merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left;//左序列指针
int j = mid + 1;//右序列指针
int t = 0;//临时数组指针
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[t++] = arr[i++];
} else {
temp[t++] = arr[j++];
}
}
while (i <= mid) {
//将左边剩余元素填充进temp中
temp[t++] = arr[i++];
}
while (j <= right) {
//将右序列剩余元素填充进temp中
temp[t++] = arr[j++];
}
t = 0;
//将temp中的元素全部拷贝到原数组中
while (left <= right) {
arr[left++] = temp[t++];
}
}
public static void main(String[] args) {
int[] arr = {
7, 1, 4, 2, 8, 3, 6, 5};
int [] temp = new int[arr.length];//在排序前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间
MergeSort04.sort(arr, 0, arr.length - 1, temp);
System.out.println("Arrays.toString(arr) = " + Arrays.toString(arr));
}
}
输出结果:
left = 0; right = 7; mid = 3; arr = [7, 1, 4, 2, 8, 3, 6, 5]
left = 0; right = 3; mid = 1; arr = [7, 1, 4, 2, 8, 3, 6, 5]
left = 0; right = 1; mid = 0; arr = [7, 1, 4, 2, 8, 3, 6, 5]
arr = [1, 7, 4, 2, 8, 3, 6, 5]
left = 2; right = 3; mid = 2; arr = [1, 7, 4, 2, 8, 3, 6, 5]
arr = [1, 7, 2, 4, 8, 3, 6, 5]
arr = [1, 2, 4, 7, 8, 3, 6, 5]
left = 4; right = 7; mid = 5; arr = [1, 2, 4, 7, 8, 3, 6, 5]
left = 4; right = 5; mid = 4; arr = [1, 2, 4, 7, 8, 3, 6, 5]
arr = [1, 2, 4, 7, 3, 8, 6, 5]
left = 6; right = 7; mid = 6; arr = [1, 2, 4, 7, 3, 8, 6, 5]
arr = [1, 2, 4, 7, 3, 8, 5, 6]
arr = [1, 2, 4, 7, 3, 5, 6, 8]
arr = [1, 2, 3, 4, 5, 6, 7, 8]
Arrays.toString(arr) = [1, 2, 3, 4, 5, 6, 7, 8]
Process finished with exit code 0
5、python代码
def merge_sort(input_list):
"""归并排序"""
n = len(input_list)
if n <= 1: # 递归结束:如果输入的列表就只有一个元素,则直接返回该元素列表,不再进行下一层的拆分与合并操作
return input_list
else: # 递归继续:如果输入的列表元素个数大于1,则继续递归进行下一层的拆分与合并操作
mid = n // 2
left_list = input_list[:mid]
right_list = input_list[mid:]
# 无序列表left_list利用归并排序方法merge_sort后形成的有序的新的列表
left_sorted_list = merge_sort(left_list)
# 无序列表right_list利用归并排序方法merge_sort后形成的有序的新的列表
right_sorted_list = merge_sort(right_list)
######## 以上代码区通过递归最终将input_list中的每个元素拆分为一个list ########
######## 接下来的步骤会将两个有序的子序列合并为一个新的有序list(从最深层到最顶层,每一次递归都合并一次) ########
# merge(left_sorted_list, right_sorted_list)
left_pointer, right_pointer = 0, 0
result_list = [] # left_sorted_list, right_sorted_list合并后的列表
while left_pointer < len(left_sorted_list) and right_pointer < len(right_sorted_list):
# 如果left_sorted_list的指针left_pointer所对应的值A比right_sorted_list的指针right_pointer所对应的值B小,则将A添加到合并后的列表result_list中,并且将left_pointer指向本列表的下一个值
if left_sorted_list[left_pointer] <= right_sorted_list[right_pointer]:
result_list.append(left_sorted_list[left_pointer])
left_pointer += 1
else:
result_list.append(right_sorted_list[right_pointer])
right_pointer += 1
# 将left_sorted_list或right_sorted_list剩下的没有加入到result_list的元素(最多一个)添加到result_list
result_list += left_sorted_list[left_pointer:]
result_list += right_sorted_list[right_pointer:]
return result_list
if __name__ == "__main__":
input_list = [54, 26, 93, 17, 77, 31, 44, 55, 20]
print('input_list=', input_list)
sorted_list = merge_sort(input_list)
print('input_list=', input_list,'原来的input_list并没有改变,排序后生成一个新列表')
print('sorted_list=', sorted_list)
七、归并排序(自底向上)-代码实现
java代码
import java.util.Arrays;
public class MergeSort04 {
// 自顶向下的归并排序
private static void sort(int[] arr, int left, int right, int[] temp) {
int n = arr.length;
// 遍历合并的区间长度
for (int size = 1; size < n; size += size) {
//遍历合并的两个区间的起始位置 i【合并[i, i + size -1] 与 [i + size, i + size * 2 -1]】
for (int i = 0; i + size < n; i += size * 2) {
merge(arr, i, i + size -1, Math.min(i + size * 2 -1, n - 1), temp);
}
}
}
// 合并两个有序的区间 arr[left, mid] 和 arr[mid + 1, right], 形成一个大的有序数组
private static void merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left;//左序列指针
int j = mid + 1;//右序列指针
int t = 0;//临时数组指针
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[t++] = arr[i++];
} else {
temp[t++] = arr[j++];
}
}
while (i <= mid) {
//将左边剩余元素填充进temp中
temp[t++] = arr[i++];
}
while (j <= right) {
//将右序列剩余元素填充进temp中
temp[t++] = arr[j++];
}
t = 0;
//将temp中的元素全部拷贝到原数组中
while (left <= right) {
arr[left++] = temp[t++];
}
}
public static void main(String[] args) {
int[] arr = {
7, 1, 4, 2, 8, 3, 6, 5};
int[] temp = new int[arr.length];//在排序前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间
MergeSort04.sort(arr, 0, arr.length - 1, temp);
System.out.println("Arrays.toString(arr) = " + Arrays.toString(arr));
}
}
输出结果:
Arrays.toString(arr) = [1, 2, 3, 4, 5, 6, 7, 8]
Process finished with exit code 0