哈密尔顿，不变的爱

前面我们提到两大变（ “变分の美”和 “Legendre变变变”），那么一直在变的话，什么时候不再变呢？这就是我们今天想概述的。所谓物极必反，又所谓螺旋式上升，再所谓三十年河东，三十年河西。一句话,变多了就想怎么不变？或者说变到不能再变！把今天所描述的"不变"想的明白的是在“变分の美” 最后提到的哈密尔顿 Hamilton.

Hamilton 是何方神圣？

William Rowan Hamilton 是来自爱尔兰（Ireland, Irish）的物理学家（1805年），数学家。老爹是个推销员，家住都柏林。 3岁那年，被狠心的老爹交由他叔叔代养，他叔叔大学毕业，算是个语言学家，拼命的给他灌输各种语言，没想到最后灌成了数学家。但这个家伙的确是个神通，5岁能读拉丁文、希腊文和希伯来文，14岁竟然掌握了12种语言。还记得《红与黑》里面的于连么？人家只会一点拉丁文就鸡窝里面飞出金凤凰了。哈密尔顿，这还得了。但是在他9岁那年，他遇上了美国速算神童Zerah Colburn，那时候美国还比较穷，来爱尔兰大都市赚钱，哈密尔顿和人家杠上了，当然是输了，人家炼过的。但是这一输，激发了少年天才拼了命的学数学。犹如滔滔江水，一发而不可收拾，在他18岁那年，进入了大学，遇上了爱尔兰天文学主席， John Brinkley博士，他这么评价18岁的哈密尔：这个年轻人，不要说将来，现在就是他这个年代NO.1的数学家（ 'This young man, I do not say will be, but is, the first mathematician of his age.'）。所以要学好数学，儿童时期，不要学数学，炼文学和记忆力吧。

你看，年轻青青，才华冠绝当世，却一辈子过得很不顺心。所谓成也萧何，败也萧何，就是这么说的。在他19岁那年（大一？），他的叔叔领着他拜访了他的一个朋友Disney。年轻的Hamilton却一见钟情，无可救药的迷恋上了人家的女儿Catherine Disney。他说Catherine是他见过唯一在思想上让他折服的女性（不知道第一见面，Catherine跟他谈了什么高大上，让Hamlitonadmired her mind）。但是那时候Hamilton家境不好，没办法搞定婚礼， 3年后，女方妈妈告诉Hamilton，女儿凯瑟琳嫁给了一位年长15岁的牧师，得到消息后的哈密尔顿极其痛苦，可能自杀过，成绩也从“极优” 滑落到了“优”（无语了），从此哈密尔顿生活痛苦，迷恋写诗发泄。或许失恋触发了哈密尔顿的无情奋斗，他成果斐然，在感情生活绝望了9年后，他找到了一个校长的女儿Helen Maria Bayly结婚了。海伦比哈密尔顿大一岁，但是一辈子并没有博得哈密尔顿的欣赏，哈密尔顿评价说“她可谓毫无智慧”。海伦身体不是很好，但是两人有二男一女。凯瑟琳晚年也过得不是很幸福，和牧师没有太多共同语言，晚年分居了，在哈密尔顿的叔叔去世那年他们开始了邮件来往。但是6年后，凯瑟琳就去世了，哈密尔顿却保持了继续和凯瑟琳家族通信，并且帮助过凯瑟琳的儿子。在凯瑟琳死前二周，哈密尔顿带着自己的四元法讲义“Lectures on Quaternions”去看了她。或许跟女神汇报自己的最佳成果。在哈密尔顿死后（活了60岁），海伦再活了4年，据说哈密尔顿死后，海伦第一次从他的朋友那里收到了无数的信件。

哈密尔顿给女神凯瑟琳最后献礼的四元数是什么？

四元数相当于复数从2维空间扩展到4维空间，并且符号化的建立了空间旋转的关系。虽然目前高维空间投影和旋转都可以基于矩阵进行建模了，但是对于4维以内的空间，四元数还是有着定制化的优势：高效，直观，容易理解。

另外，基于四元数对Cayley Graph克雷图的理解，在算法应用上也有极大帮助。例如如何非递归求解全排列？其中一种方式就是利用Cayley 图。

如何走近哈密尔顿？

哈密尔顿最斐然的成果是哈密尔顿系统的建立，是自牛顿系统之后又一个伟大的突破。据说，你站在泰勒Taylor的肩膀上，跨过拉格朗日Larange（参考“一步一步走向锥规划 - QP”），再携手勒让德Legendre（参考“Legendre变变变”），你就找到了哈密尔顿Hamilton。

突破变，就是对爱的不变

哈密尔顿做到了，最早源于他对傅里叶分析（Fourier analysis）的喜爱。我们知道还有一位大神，最早学文学的（历史系），然后上了一堂傅里叶变换的课程，从而喜欢上了数学，他就是Andrey Kolmogorov。Fourier变换也是一种典型的从变中找不变的神器。

如何为任意函数建模？

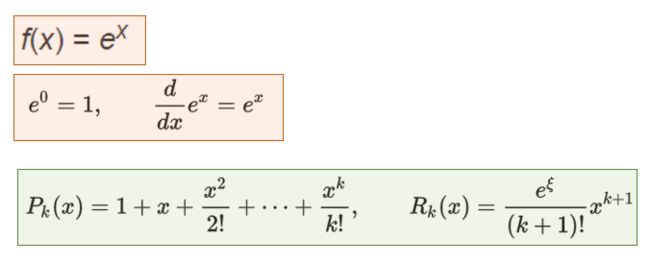
我们知道，泰勒展开提供了对任意连续光滑函数（smooth function）的多项式（polynomials ）叠加的拟合，这种拟合可以到任意精度要求，并且可以根据需求对余项（remainder）多种表达形式。

举个指数函数的列子：

再举一个三角函数（sine）的例子（sin（x））：

所以，我们要表达一个任意函数，我们只要提供各阶导数，然后我们就可以利用多项式进行按精度要求的拟合。

那么根据泛函的思想，参考“变分の美”，如果利用一阶泰勒展开，要变换函数，只要变换x,f(x),f'(x)，就可以了。

如何引入泛函目标表达式？

我们有了函数的任意表示，那么把函数看成输入参数，然后建立目标公式，我们就得到了拉格朗日量（Lagrangian）：

那么根据EL公式Euler-Larange Equation的思想，参考“变分の美”，可以得到向量化（vectorization）后的公式。

至此，我们离哈密尔顿的不变就差不太远了。

哈密尔顿原理的引入

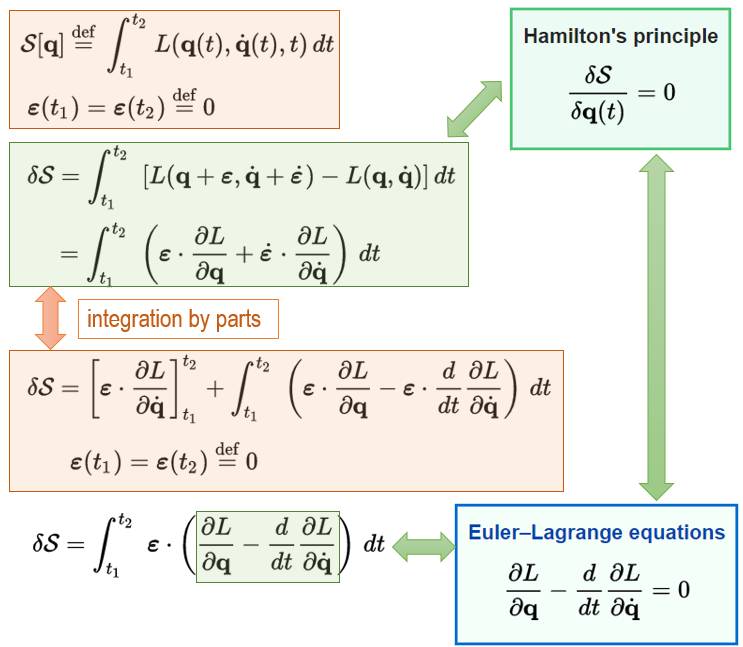
根据向量化的欧拉公式，可以引入哈密尔顿原理（Hamilton Principle）了。

就是积分系统的对于泛函的变换为零。

在这个推演过程中，要用到一个变分法的基础引理（fundamental lemma of caculus of variations）：

哈密尔顿原理带来了什么变化？

这样我们从牛顿系统，到了拉格朗日系统，再到了哈密尔顿系统，那整个这个过程到底做了什么？

从牛顿系统到拉格朗日系统，坐标系更为通用，并且引入了泛函。而从拉格朗日系统到哈密尔顿系统，引入了作用量 action integral，并且不再受到坐标系的限制。

作用量积分是什么？

作用量积分（action integral）是对拉格朗日量（lagrangian）在两个不动点（stationary points）上的积分。而哈密尔顿原理告诉我们，这样的积分的变化为零，也就是说是个不动的静态的作用量（stationary action）。

作用量积分有什么用呢？

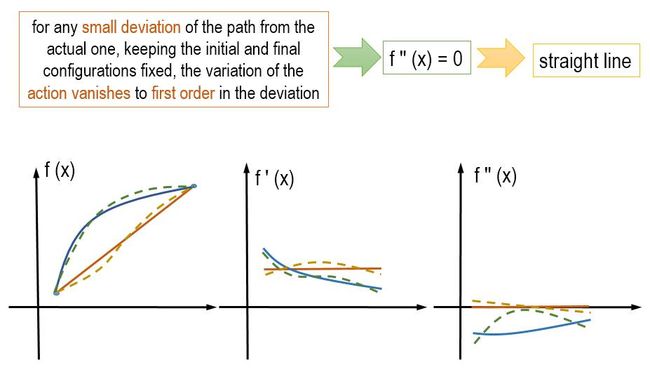
在把作用量（action）定义成积分的形式后，很明显，不同的路径q(t)会带来作用量的不一致。正是作用量对积分路径的依赖，使得哈密尔顿的方法变得有意义。为什么呢？哈密尔顿原理说，存在一条路径使得作用量是静止stationary。就是说这条路径发生一个极小的偏差，在拉格朗日量一阶导的情况下，带来的作用量的变化可以忽略不计。这又是什么含义呢？

在“变分の美”里面有最短的是直线的证明，那么我们用这个例子，按哈密尔顿原理，直接进行解释。哈密尔顿原理要求的那条路径，发生一个极小的偏差，但是带来的作用量变化可以忽略不计。因为作用量是对拉格朗日量的积分，如果拉格朗日量的三个参量（x, f(x),f'(x)）的变化都可以忽略不计，那么可以是看成作用量变化可以忽略。因为本来是很小的偏差，那么f(x)的变化可以看成不变。但是f'(x)的变换是f''(x)。因此我们看到哈密尔顿原理对路径的要求，蕴含着f''(x)为零。在这种情况下很容易知道，两点之间的直线路径满足这个要求。

什么是广义的坐标系（generalized coordinates）？

首先我们知道坐标系有直角正交坐标系和极坐标系。而广义坐标系就是进一步放宽限制。例如非欧几何里面就在曲面上建坐标系。

更直观的，如果固定对线的限制，对角的描述就会很不一样。

我们知道，牛顿系统定理的描述必须要求独立正交的坐标系。但是在拉格朗日系统定理的描述，就能扩展到这些广义的坐标系。这样有两个好处：可以随意的换适合对问题描述的坐标系。可以解决一些受牛顿系统描述限制而无法解决的问题。其实，这其中已经蕴含了对变化的系统去追求不变的道理的思想。

不要坐标系（nocoordinates）又指什么呢？

我们现在很清楚拉格朗日系统是如何突破了牛顿系统的，那么哈密尔顿系统又是如何突破拉格朗日系统的呢？

因为哈密尔顿系统直接利用了导数和积分来对变化直接建模，使得好多不需要坐标系，但是又存在导数和积分的系统都可以使用哈密尔顿系统建模，譬如能量，熵，势，角动量等等。所以哈密尔顿力学Hamiltonian mechanics和哈密尔顿场论Hamiltonian field theory都有突破。哈密尔顿场论除了广义坐标系，还对共轭动量conjugate momenta, 和时间time都有扩展。而哈密尔顿力学主要突破就是对Symplectic manifold 辛流形（一个辛流形上的任何实值可微函数H可以用作一个能量函数或者叫哈密顿量。和任何一个哈密顿量相关有一个哈密顿向量场；该哈密顿向量场的积分曲线是哈密顿-雅可比方程的解。哈密顿向量场定义了辛流形上的一个流场，称为哈密顿流场或者叫辛同胚。）引入。

但是要注意，量子力学Quantum mechanics和量子场Quantum field theory的发展突破了经典的哈密尔顿力学和哈密尔顿场论，最主要的是经典的还是属于确定性determinism的范畴，而量子理论基本是概率范畴（著名的薛定谔猫）。譬如，在最优路径上，不是一条明确的路径，而是按概率的无数条路径。一句话，最大的差别是哈密尔顿主要还属于经典范畴。