余弦定理和新闻的分类

世界上有些事情常常超乎人们的想象。余弦定理和新闻的分类似乎是两件八杆子打不着的事，但是它们确有紧密的联系。具体地说，新闻的分类很大程度上依靠的是余弦定理。

早在2002年夏天，Google就推出了自己的"新闻"服务。和传统媒体的做法不同，这些新闻不是记者写的，也不是人工编辑的，而是由计算机整理、分类和聚合各个新闻网站的内容，一切都是自动生成的。这里面的关键技术就是新闻的自动分类。

1. 新闻的特征向量：

所谓新闻的分类，或者更广义地讲任何文本的分类，无非是要把相似的新闻放到同一类中。如果让编辑来对新闻分类，他—定是先把新闻读懂，然后找到它的主题，最后根据主题的不同对新闻进行分类。但是计算机根本读不懂新闻，虽然一些商业人士和爱炫耀自己才学的计算机专家宣称计算机能读懂新闻。计算机本质上只能做快速计算。为了让计算机能够"算"新闻（而不是读新闻），就要求我们首先要把文字的新闻变成可以计算的一组数字，然后再设计一个算法来算出任意两篇新闻的相似性。

首先让我们来看看怎样找一组数字（或者说一个向量）来描述一篇新闻。新闻是传递信息的，而词是信息的载体，新闻的信息和词的语义是联系在一起的。套用俄罗斯文豪托尔斯泰在《安娜·卡列尼娜》开篇的那句话工来讲，"同一类新闻用词都是相似的，不同类的新闻用词各不相同"。当然，一篇新闻有很多词，有些词表达的语义重要，有些相对次要。那么如何确定哪些重要，哪些次要呢? 首先，直觉告诉我们含义丰富的实词一定比"的、地、得"这些助词，或者"之乎者也"这样的虚词重要这点是肯定的。接下来，需要进一步对每个实词的重要性进行度量。在一篇文章中，重要的词TF- IDF值就高。不难想象，和新闻主题有关的那些实词频率高，TF-IDF值很大。

现在我们找到了一组来描述新闻主题的数字∶ 对于一篇新闻中的所有实词，计算出它们的 TF-IDF 值。把这些值按照对应的实词在词汇表的位置依次排列，就得到一个向量。比如，词汇表中有 64 000个词，其编号和词如下图所示：

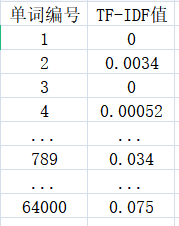
在某一篇特定的新闻中，这 64000 个词的 TF-IDF 值分别如下图 所示：

如果单词表中的某个词在新闻中没有出现，对应的值为零，那么这 64000 个数，组成一个64000 维的向量。我们就用这个向量来代表这篇新闻，并成为新闻的特征向量（Feature Vector）。每一篇新闻都可以对应这样一个特征向量，向量中每一个维度的大小代表每个词对这篇新闻主题的贡献。当新闻从文字变成了数字后，计算机就有可能"算一算"新闻之间是否相似了。

一篇篇文章变成了一串串数字：

 

2. 向量距离的度量：

世界各国无论是哪门语言的"语文课"（Language Art），老师教授写作时都会强调特定的主题用特定的描述词。几千年来，人类已经形成了这样的写作习惯。因此，同一类新闻一定是某些主题词用得较多，另外一些词则用得少。比如金融类的新闻，这些词出现的频率就很高;股票，利息，债券，基金，银行，物价，上涨。而这些词出现的就少∶ 二氧化碳，宇宙，诗歌，木匠，诺贝尔，包子。反映在每一篇新闻的特征上，如果两篇新闻属于同一类，它们的特征向量在某几个维度的值都比较大，而在其他维度的值都比较小。反过来看，如果两篇新闻不属于同一类，由于用词的不同，它们的特征向量中，值较大的维度应该没有什么交集。这样就定性地认识到两篇新闻的主题是否接近，取决于它们的特征向量"长得像不像"。当然，我们还需要定量地衡量两个特征向量之间的相似性。

不同的新闻，因为文本长度的不同，它们的特征向量各个维度的数值也不同。一篇 10000 字的文本，各个维度的数值都比一篇 500 字的文本来得大，因此单纯比较各个维度的大小并没有太大意义。但是，向量的方向却有很大的意义。如果两个向量的方向一致，说明相应的新闻用词的比例基本一致。因此，可以通过计算两个向量的夹角来判断对应的新闻主题的接近程度。而要计算两个向量的夹角，就要用到余弦定理了。比如上图中，左边两个向量的夹角小，距离就较"近"，相反，右边两个向量的夹角大，距离就"远"。

3. 余弦定理：

我们对余弦定理都不陌生，它描述了三角形中任何一个夹角和三个边的关系，换句话说，给定三角形的三条边，可以用余弦定理求出三角形各个角的角度。假定三角形的三条边为a，b和c，对应的三个角为A，B和C。

那么的余弦是： 。

如果将三角形的两边b和c看成是两个以A为起点的向量，那么上述公式等价于  。

其中，分母表示两个向量b和c的长度，分子表示两个向量的内积。举一个具体的例子，假如新闻X和新闻Y对应的向量分别是： 和 。

那么它们夹角的余弦等于：

由于向量中的每一个变量都是正数，因此余弦的取值在 0和1 之间，也就是说夹角在 0 度到 90 度之间。当两条新闻向量夹角的余弦等于1时，这两个向量的夹角为零，两条新闻完全相同;当夹角的余弦接近于1时，两条新闻相似，从而可以归成一类;夹角的余弦越小，夹角越大，两条新闻越不相关。当两个向量正交时（90 度），夹角的余弦为零，说明两篇新闻根本没有相同的主题词，它们毫不相关。

现在把一篇篇文字的新闻变成了按词典顺序组织起来的数字（ 特征向量），又有了计算相似性的公式，就可以在此基础上讨论新闻分类的算法了。余弦定理就这样通过新闻的特征向量和新闻分类联系在一起。我们在中学学习余弦定理时，恐怕很难想象它可以用来对新闻进行分类。

补充：什么是TF-IDF:

TF-IDF(Term Frequency - Inverse Document Frequency, 单文本词频-逆文本频率指数)，一种用于信息检索和信息探勘的常用加权技术，被公认为信息检索中最重要的发明。

TF-IDF是一种统计方法，用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比下降。TF-IDF加权的各种形式常被搜寻引擎应用，作为文件与用户查询之间相关程度的度量或评级。

词频(Term Frequency)：某一给定词语在该文本中出现次数。该数字通常会被归一化（分子一般小于分母），以防止它偏向长的文件，因为不管该词语重要与否，它在长文件中出现的次数很可能比在段文件中出现的次数更大。需要注意的是有一些通用词对文章主题没有太大作用，如“的”、“是”等，而有一些频率出现少的词如一些专业词更能表现文章主题，所以为词语设置权重，权重的设计满足：一个词预测主题的能力越强，权重越大，反之，权重越小。也就是说，一些词只在很少几篇文章中出现，那么这样的词对文章主题的判断能力很大，这些词的权重应该设计的较大。IDF完成这样的工作。

逆向文件频率IDF（Inverse Document Frequency）：一个词语普遍重要性的度量。主要思想是：如果包含一个词条的文档越少, IDF越大，则说明词条具有很好的类别区分能力。

可以简单的理解成：一个词语在一篇文章中出现的次数越多，同时在其他的所有文档中出现的次数越少，越能够代表该文章。

读者可以自行去查阅资料，了解TF-IDF的具体计算方法和基于信息论的基本原理。

结语：

本文旨在简单的介绍余弦定理与新闻分类的联系，也就是数学和计算机科学的交叉。在我们看来复杂的计算机处理工程中，其中蕴含的原理可能就是一个简单的数学公式，数学有着简单美的特性，计算机科学也有，文章主要参考了吴军博士的《数学之美》，吴军博士遵循着简单的哲学，倡导要努力去寻找简单有效的方法，不是靠直觉，更不是撞大运，而是要靠自己的经验，不怕失败，大胆尝试，总会有所收获的。

 

Everything is difficult until you know how to do it.