DS:树-二叉树-二叉堆（详解+实例）

树

• 节点的度:一个节点上含有子树的个数；
• 叶/终端节点:度为0的节点；
• 双亲/父节点:对于其子节点来说的；
• 子节点:对于其所属分支的上属节点来说；
• 兄弟节点:具有相同父节点；
• 数的度:最大的节点的度；
• 节点层次:从根节点开始为第一层，其子节点为第二层…
• 堂兄节点:父节点同层；
• 节点祖先：该分支上所有之前的节点；

定义(孩子兄弟表示法)

typedef int DataType;
typedef struct Node{
     
  struct Node* firstChild;//长子节点；
  struct Node* pNextBrother;//横向表示兄弟；
  DataType data;
}

• 应用于文件存储；

二叉树

• 是一颗有序树:左子树不等于右子树时，左右子树互换后该树不相等；

存储结构

链式表示法

typedef struct TreeNode{
     
    int val;
    struct TreeNode *left;//左子树的根节点
    struct TreeNode*right;//右子树的根节点；
}TreeNode;
typedef  struct TreeNode{
     
    int val;
    struct TreeNode *left;//左子树的根节点
    struct TreeNode*right;//右子树的根节点；
    struct TreeNode*parent;//指向其双亲节点；
}TreeNofe;

• 满二叉树:一个二叉树，如果每一层节点都达到最大值，则这个二叉树就是满二叉树-》k层，节点数是(2^k)-1，特殊的完全二叉树；上面所有层节点之和=本层节点之和；
• 完全二叉树:效率高；出最后一层之外节点都是满的，最后一层的节点都集中在左侧；不得的出现左为空右有子；

遍历方式

深度优先遍历

前序遍历(进来)

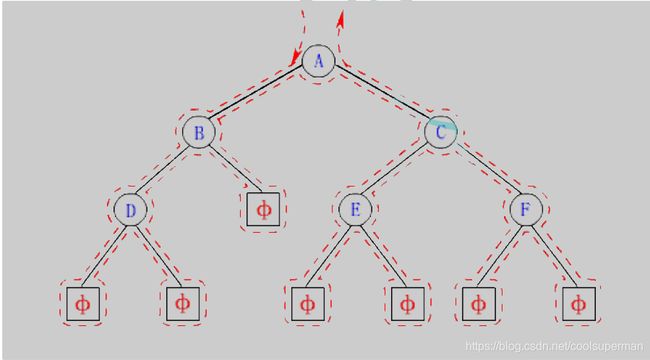
• A-B-D-C-E-F
  递归思想(根->左->右)
• A根->B左–>C右
• B->D左->NULL右
• D->NULL左->NULL右
• C->E左->F右
• E->NULL->NULL
• F->NULL->NULL

void preorder(TreeNode*root){
     
     if(root==NULL){
     
         return ;
     }
      printf("%d",root->val);
      preorder(root->left);
      preorder(root->right);
}

中序遍历(中间)

• D-B-A-E-C-F
  递归思想(左->根->右)
• D->B->NULL
• B->A->NULL
• A->=->C
• E->C->F
• C->=->F
• F->=->NULL

后序遍历(出去)

• D-B-E-F-C-A
  递归思想(左->右->根)
• D->NULL->B
• B->C->A
• E->F->C
• NULL->F->C
• =->C->A
• A
  前序与后序:无法分辨左右子树，方便找根；中序：方便区分左右子树；没法找根

广度优先遍历

层序遍历（使用链表）

• A-B-C-E-F
• 处理节点时，将其子节点放入队列中去:

void LevellorderTraversal(TreeNode*root){
     
     //队列里面存节点地址；
     if(root==NULL){
     
        return ;
     }
     QueuePush(queue,root);
     while(QueueEmpty(queue)){
     
           TreeNode*front = QueueFront(queue);
           QueuePop(queue);
           printf("%c",front->val);
           if(front->left!=NULL){
     
              QueuePush(front->left);
           }
           if(front->right!= NULL){
     
              QueuePush(front->right);
           }
     }
}

求二叉树中所有节点的个数

void TreeSize(TreeNode*root,int*size){
     
     if(root==NULL){
     
          return ;
     }
     TreeSize(root->left);
     (*size)++;
     TreeSize(root->right);
}//中序遍历思想
int TreeSize(TreeNode*root,){
     
    if(root==NULL){
     
       return 0;
    }
    return 1+TreeSize(root->left)+TreeSize(root->right);
}//递推思想

求二叉树叶子节点个数

void LeafSize(TreeNode*root,int*size){
     
     if(root==NULL){
     
         return;
     }
     if(root->left==NULL&&root->rignt==NULL){
     
         (*size)++:
     }
     LeafSize(root->left);
     LeafSize(root->right);
}//添加判断条件遍历即可；
int LeafSize2(TreeNode*root){
     
     if(root==NULL){
     
        return 0;
     }
     if(root->left==NULL&&root->right==NULL){
     
        return 1;
     }
     return LeafSize2(root->left)+LeafSize2(root->right);
}

求第k层节点个数

int LevelSize(TreeNode*root,int k){
     
     if(root==NULL){
     
        return 0;
     }
     if(k==1){
     
           return 1;
     }
     return LevelSize(root->left,k-1)+LevelSize(root->right,k-1);
}

在二叉树中查找一个值(递推思路)

TreeNode*Find(TreeNode*root,char x){
     
   if(root==NULL){
     
      return NULL;
   }
   if(root->val==x){
     
      return root;
   }
   TreeNode*get_left = Find(root->left,x);
   if(get_left!=NULL){
     
      return get_left;
   }
   return  Find(root->right,x);
}

判断二叉树是否是完全二叉树（层序遍历）

• 特点，从左至右从上至下，如果有一节点为空，其余后节点都为空，只有最后一层可能出现非满；

1. 将根节点地址放入队列；
2. 从对手取出节点地址；
3. 判断节点是否为空，空break；
4. 将左孩子放入队列中无论是否为空，将右孩子放到队列中无论是否为空
5. 如果跳出队列，检查剩余数据是否为空，如果为空:完全二叉树，如果不为空，非完全二叉树

bool IsCompleteBinaryTree(TreeNode*root){
     
    if(root==NULL){
     
        return true;
    }
     QueuePush(queue,root);
     while(QueueEmpty(queue)){
     
           TreeNode*front = QueueFront(queue);
           QueuePop(queue);
            if()front==NULL){
     
                break;
            }
              QueuePush(front->left);
              QueuePush(front->right);
     }
     while(QueueEmpty(queue)){
     
        TreeNode *front=QueueFront(queue);;
         QueuePop(queue);
         if(front!=NULL){
     
             return false;
         }
     }
}

二叉树前序|中序|后序非递归写法(自行用栈实现)

void PreorderTraversalNor(TreeNode*root){
     //前序
    TreeNode *cur = root;
    TreeNode*top；
    TreeNode*last = NULL
    std::stack<TreeNode*> st;
    while(!st.empty()||cur!=NULL){
     
      while (cur!=NULL){
     
      //第一次访问节点:cur;
      printf("%c",cur->val)//前序
      st.push(cur);
      cur = cur->left;
     }
      top = st.top();//从栈顶取元素
      if(top->right!=NULL&&top->right!=last){
     
          cur = top->right;//第二次访问节点：top；如果其右子节点被pop则说明到了第三次；
           printf("%c",cur->val)//中序,注意在右边无子树二三一起进行，所以单独打印一次
      }
       if(top->right==NULL){
     
           printf("%c",cur->val)//中序
       }
      else{
     
         printf("%c",cur->val)//后序
         st.pop();//第三次访问节点:top;
         last= top;
      }
    }
}

tips：

• 递推的思路（所有问题）:根+左子树+右子树
  终止条件：

1. 二叉树的五种形态；
   2.可能的其他情况；

• 遍历的思路:
• 前序|中序|后序|层序，遍历的同时找到第一次，第二次，第三次访问点然后操作；

顺序实现法(二叉堆)

• 逻辑上是一颗完全二叉树；(但这种完全二叉树上任意一个节点root，root的val>=两个孩子的val(大堆)，或<=两个孩子的val(小堆))
• 物理上顺序存储(数组)
• 功能:找数据中的最值

	已知[parent]		已知[child]
左子树	2*[parent]+1	双亲节点	([child]-1)/2
右子树	2*[parent]+2

调整二叉堆

小堆调整

• 要调整[root]所在的节点
  • 前提：[root]的左右子树已经满足堆的性质；
    • 如果root已经是叶子节点，调整结束；
• 找到左右孩子中最小的一个[min]
• if arry[root]<=arry[min];
  • else:swap(&arry[root],&arry[min])
  • [min] = [root];循环；

void AdjustDown(int array[],int Size,int root){
     
     //因为为完全二叉树，所以没有左孩子一定没有有孩子；
    while(1){
     
        int left = 2*root+1;
     if(left>=Size){
     
        return;
     }
    //一定有左孩子，但不一定有有右孩子；
    int right = 2*root+2；
    int min = left
    if(rightt<Size&&array[right]<array[left]){
     
         min = right;
    }
    if(array[min]>array[root]){
     
        return;
    }
    int t =array[min];
    array[min] = array[root];
    array[root] = t;
    root = min;//继续向下调整；
    }
}

定义&初始化

typedef struct Heap{
     
     int arrar[100];
     int size;
}Heap;
//最后一个非叶子节点=最后一个节点的双亲节点；
void CreatHeap(int arry[],int size){
     
     for(int i = ((size-1)-1)/2;i>=0;i--){
     
          AdjustDown(array,size,i);
     }
}//从最后一个非叶子节点开始向下调整；
void HeapInit(Heap*heap,int array[],int size){
     
      memcpy(heap->array,array,size*sizeof(int));
      heap->size = size;
      CreatHeap(heap->arry,size);
}

插入(尾插)

向上调整

void AdjustUp(int arry[],int size,int child){
     
   int i = child;
   while (i){
     
       int parent = (i-1)/2;
       if(array[parent]<=array[i]){
     
              return;
       }
       int temp = array[i];
       array[i] = array[parent];
       array[parent] = temp;
       i = parent;
   }
}
void HeapPush(Heap*heap,int val){
     
    heap->array[heap->size++] = val;
    AdjustUp(heap->array,heap->size,heap->size-1);
}

删除(尾删)

• 如果直接删除元素，会直接破坏堆的结构。所以将最后一个叶子节点覆盖到你要替换的元素位置，在进行向下调整；

void HeapPop(Heap*heap){
     
      heap->[0] = heap->array[heap->Size-1];
      AdjustDown(heap->array,heap->Size-1,0);
      heap->Size--
}

返回队顶元素

int HeapTop(Heap*heap){
     
     return heap->array[0];
}

堆排序

• 排升序建大堆，派降序建小堆；
  • 因为这样调整回堆的成本更小；

void HeapSort(int arr[],int size){
     
    CreatHeap(arr,size);
    for(int i =0;i<size-1;i++){
     //得进行size-1次寻找；
        int t = arr[0];
        arr[0] = arr[size-i-1];
        arr[size-i-1] = t;//交换堆顶和堆尾
        AdjustDown(arr,size-i-1,0);//向下调整，数据规模-1；
    }
}//O(n*logn)