《李航 统计学习方法》学习笔记——第九章EM算法及其推广
EM算法及其推广
- 9.1 EM算法
-
- 9.1.1 EM算法介绍
- 9.1.2 EM算法推导
- 9.2 EM算法的收敛性
- 9.3 EM算法在高斯混合模型学习下的应用
-
- 9.3.1 高斯混合模型GMM
- 9.3.2 高斯混合模型参数估计的EM算法
- 9.4 EM算法的推广
-
- 9.4.1 F F F函数的极大-极大算法
- 9.4.2 GEM算法
- 习题9.1python实现
- 习题9.2
- 习题9.3 python实现
- 习题9.4 混合贝叶斯模型
- 参考
9.1 EM算法
适用于无监督学习。训练数据只有输入没有对应的输出,可以认为无监督学习的训练数据是联合概率分布产生的数据。
应用场景:引自博主
如果我们要求解的是一个混合模型,只知道混合模型中各个类的分布模型(譬如都是高斯分布)和对应的采样数据,而不知道这些采样数据分别来源于哪一类(隐变量),那这时候就可以借鉴EM算法。EM算法可以用于解决数据缺失的参数估计问题(隐变量的存在实际上就是数据缺失问题,缺失了各个样本来源于哪一类的记录)
9.1.1 EM算法介绍
EM算法:含有隐变量的概率模型参数的极大似然估计法或极大后验概率估计法。每次迭代分为E步(极大期望)和M步(求极大)。
三硬币模型

在这个实例中,抛硬币A的结果(这里记为Z )是无法观测的,所以该结果称之为隐变量。
在该例子中,也可以称(Y,Z)为完全数据,Y为不完全数据
设随意变量Y为观测到的抛硬币的结果(即观测变量), θ = ( π , p , q ) \theta=(\pi,p,q) θ=(π,p,q)是模型参数,则可以得到模型的似然函数(因为这里是离散变量,所以是求和,连续变量则为求积分):
P ( Y ∣ θ ) = ∑ Z P ( Z ∣ θ ) P ( Y ∣ Z , θ ) = ∏ j = 1 n [ π p y j ( 1 − p ) 1 − y j + ( 1 − π ) q y j ( 1 − q ) 1 − y j ] P(Y|\theta)=\sum\limits_ZP(Z|\theta)P(Y|Z,\theta)\\ =\prod\limits_{j=1}^n\left [ \pi p^{y_j}(1-p)^{1-y_j}+(1-\pi)q^{y_j}(1-q)^{1-y_j} \right ] P(Y∣θ)=Z∑P(Z∣θ)P(Y∣Z,θ)=j=1∏n[πpyj(1−p)1−yj+(1−π)qyj(1−q)1−yj]
按照正常的求解过程,对参数 θ \theta θ进行极大似然估计,即:
θ = arg max θ log P ( Y ∣ θ ) \theta = \arg\max\limits_{\theta}\log P(Y|\theta) θ=argθmaxlogP(Y∣θ)
这个问题没有解析解,因为模型中既有未知变量Z也有模型变量 θ \theta θ。只能通过迭代计算参数的估计值。EM算法就是用于求解这种问题的迭代算法。
算法9.1 EM算法
输入:观测数据变量Y,隐变量数据Z,联合分布P(Y,Z| θ \theta θ),条件分布P(Z|Y, θ \theta θ)
输出:模型参数 θ \theta θ
(1)选择参数的初值 θ ( 0 ) \theta^{(0)} θ(0),开始迭代;
(2)E步:记 θ ( i ) \theta^{(i)} θ(i)为第i此迭代参数 θ \theta θ的估计值,在第i+1此迭代的E步,计算
Q ( θ , θ ( i ) ) = E Z [ log ( P ( Y , Z ∣ θ ) ∣ Y , θ ( i ) ] = ∑ Z log ( P ( Y , Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) Q(\theta,\theta^{(i)})=E_Z\left [ \log(P(Y,Z|\theta)|Y,\theta^{(i)} \right]\\ = \sum_Z\log(P(Y,Z|\theta)P(Z|Y,\theta^{(i)}) Q(θ,θ(i))=EZ[log(P(Y,Z∣θ)∣Y,θ(i)]=Z∑log(P(Y,Z∣θ)P(Z∣Y,θ(i))
上式子的思想主要为:由于Zi是隐变量,为了能够计算 θ \theta θ是排除其他可变量,所以通过利用固定值Z的期望代替变量Zi求近似极大化,即 Z i → E ( Z ) Z_i \rightarrow E(Z) Zi→E(Z) Q函数的意义为在给定观测数据Y和当前参数 θ ( i ) \theta^{(i)} θ(i)下对为观测数据Z的条件概率分布 P ( Z ∣ Y , θ ( i ) ) P(Z|Y,\theta^{(i)}) P(Z∣Y,θ(i))的期望。Q中的第一个变元表示要极大化的参数,第二个变元表示当前该参数的估计值。每次迭代的最终目的为求Q函数的极大。
(3)M步:求使得 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i))极大化的 θ \theta θ,确定第i+1次的迭代的参数估计值 θ ( i + 1 ) \theta^{(i+1)} θ(i+1):
θ ( i + 1 ) = arg max θ Q ( θ , θ ( i ) ) \theta^{(i+1)} =\arg\max_\theta Q(\theta,\theta^{(i)}) θ(i+1)=argθmaxQ(θ,θ(i))
每一次迭代产生 θ ( i + 1 ) \theta^{(i+1)} θ(i+1),会使得似然函数增大或达到局部极值。
(4)重复(2)(3)直到收敛。(较小的正数 ε 1 , ε 2 \varepsilon_1,\varepsilon_2 ε1,ε2,若满足:
∣ ∣ θ ( i + 1 ) − θ ( i ) ∣ ∣ < ε 1 o r ∣ ∣ Q ( θ ( i + 1 ) , θ ( i ) ) − Q ( θ ( i ) , θ ( i ) ) ∣ ∣ < ε 2 ||\theta^{(i+1)}-\theta^{(i)}||<\varepsilon_1\\ or\\ ||Q(\theta^{(i+1)},\theta^{(i)})-Q(\theta^{(i)},\theta^{(i)})|| < \varepsilon_2 ∣∣θ(i+1)−θ(i)∣∣<ε1or∣∣Q(θ(i+1),θ(i))−Q(θ(i),θ(i))∣∣<ε2
则停止迭代。)
9.1.2 EM算法推导
模型目标:极大化观测数据Y关于参数 θ \theta θ的对数似然函数,即极大化:
L ( θ ) = log P ( Y ∣ θ ) = log ∑ Z P ( Y , Z ∣ θ ) = log ( ∑ Z P ( Y ∣ Z , θ ) P ( Z ∣ θ ) ) L(\theta)=\log P(Y|\theta)=\log\sum_Z P(Y,Z|\theta)\\ =\log(\sum_ZP(Y|Z,\theta)P(Z|\theta)) L(θ)=logP(Y∣θ)=logZ∑P(Y,Z∣θ)=log(Z∑P(Y∣Z,θ)P(Z∣θ))
在极大化的过程中,因为涉及到隐变量Z未知,所以极大化求解困难。
所以EM的主要思想是迭代逐步近似极大化 L ( θ ) L(\theta) L(θ)。
假设新估计值 θ \theta θ,上一次的估计值 θ ( i ) \theta^{(i)} θ(i),为了每次迭代能够使得极大值尽可能增加,所以这里考虑每次迭代对数似然函数的增加量:
L ( θ ) − L ( θ ( i ) ) = log ( ∑ Z P ( Y ∣ Z , θ ) P ( Z ∣ θ ) ) − log P ( Y ∣ θ ( i ) ) = log ( ∑ Z P ( Z ∣ Y , θ ( i ) ) P ( Y ∣ Z , θ ) P ( Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) ) − log P ( Y ∣ θ ( i ) ) L(\theta)-L(\theta^{(i)})=\log(\sum_ZP(Y|Z,\theta)P(Z|\theta))-\log P(Y|\theta^{(i)})\\ =\log(\sum_ZP(Z|Y,\theta^{(i)})\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})})-\log P(Y|\theta^{(i)}) L(θ)−L(θ(i))=log(Z∑P(Y∣Z,θ)P(Z∣θ))−logP(Y∣θ(i))=log(Z∑P(Z∣Y,θ(i))P(Z∣Y,θ(i))P(Y∣Z,θ)P(Z∣θ))−logP(Y∣θ(i))
Jensen不等式:
log ∑ j λ j y j ⩾ ∑ j λ j log y i λ j ⩾ 0 a n d ∑ j λ j = 1 \log\sum_j\lambda_jy_j\geqslant\sum_j\lambda_j\log y_i \\ \lambda_j \geqslant 0 \ \ and \ \ \sum_j\lambda_j=1 logj∑λjyj⩾j∑λjlogyiλj⩾0 and j∑λj=1
利用以上不等式可以变形为
L ( θ ) − L ( θ ( i ) ) ⩾ ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y ∣ Z , θ ) P ( Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) − log P ( Y ∣ θ ( i ) ) = ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y ∣ Z , θ ) P ( Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) P ( Y ∣ θ ( i ) ) L(\theta)-L(\theta^{(i)}) \geqslant \sum_ZP(Z|Y,\theta^{(i)})\log\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})}-\log P(Y|\theta^{(i)})\\ =\sum_ZP(Z|Y,\theta^{(i)})\log\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})P(Y|\theta^{(i)})} L(θ)−L(θ(i))⩾Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ(i))P(Y∣Z,θ)P(Z∣θ)−logP(Y∣θ(i))=Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ(i))P(Y∣θ(i))P(Y∣Z,θ)P(Z∣θ)
把 L ( θ ( i ) ) L(\theta^{(i)}) L(θ(i))移向到等号右侧,令:
B ( θ , θ ( i ) ) = L ( θ ( i ) ) + ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y ∣ Z , θ ) P ( Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) P ( Y ∣ θ ( i ) ) B(\theta,\theta^{(i)}) = L(\theta^{(i)})\ + \ \sum_ZP(Z|Y,\theta^{(i)})\log\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})P(Y|\theta^{(i)})} B(θ,θ(i))=L(θ(i)) + Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ(i))P(Y∣θ(i))P(Y∣Z,θ)P(Z∣θ)
得到下界 L ( θ ) L(\theta) L(θ)的一个下界 B ( θ , θ ( i ) ) B(\theta,\theta^{(i)}) B(θ,θ(i)):
L ( θ ) ⩾ B ( θ , θ ( i ) ) L(\theta)\geqslant B(\theta,\theta^{(i)}) L(θ)⩾B(θ,θ(i))
因此,任意一个使得下界增大的 θ \theta θ,也可以使似然函数增大,所以为了似然函数尽可能大的增长,应选择 θ ( i + 1 ) \theta^{(i+1)} θ(i+1)使得下界达到极大:
θ ( i + 1 ) = arg max θ B ( θ , θ ( i ) ) \theta^{(i+1)} =\arg\max_\theta B(\theta,\theta^{(i)}) θ(i+1)=argθmaxB(θ,θ(i))
在求解该式子中,省去一些不包含 θ \theta θ变量得常数项,得:
θ ( i + 1 ) = arg max θ ( L ( θ ( i ) ) + ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y ∣ Z , θ ) P ( Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) P ( Y ∣ θ ( i ) ) ) = arg max θ ( ∑ Z P ( Z ∣ Y , θ ( i ) ) log P ( Y ∣ Z , θ ) P ( Z ∣ θ ) ) 保 留 了 P ( Z ∣ Y , θ ( i ) ) 该 常 数 项 = arg max θ ( ∑ Z P ( Z ∣ Y , θ ( i ) ) log ( P ( Y , Z ∣ θ ) ) = arg max θ Q ( θ , θ ( i ) ) \theta^{(i+1)} = \arg\max_\theta(L(\theta^{(i)})\ + \ \sum_ZP(Z|Y,\theta^{(i)})\log\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})P(Y|\theta^{(i)})})\\ =\arg\max_\theta(\sum_ZP(Z|Y,\theta^{(i)})\log{P(Y|Z,\theta)P(Z|\theta)}) 保留了P(Z|Y,\theta^{(i)})该常数项\\ =\arg\max_\theta(\sum_ZP(Z|Y,\theta^{(i)})\log(P(Y,Z|\theta))\\ =\arg\max_\theta Q(\theta,\theta^{(i)}) θ(i+1)=argθmax(L(θ(i)) + Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ(i))P(Y∣θ(i))P(Y∣Z,θ)P(Z∣θ))=argθmax(Z∑P(Z∣Y,θ(i))logP(Y∣Z,θ)P(Z∣θ))保留了P(Z∣Y,θ(i))该常数项=argθmax(Z∑P(Z∣Y,θ(i))log(P(Y,Z∣θ))=argθmaxQ(θ,θ(i))
到这里完成了EM算法得一次迭代,即Q函数得极大化。方式:通过不断求解下界得极大化逼近求解对数似然函数极大化得算法。
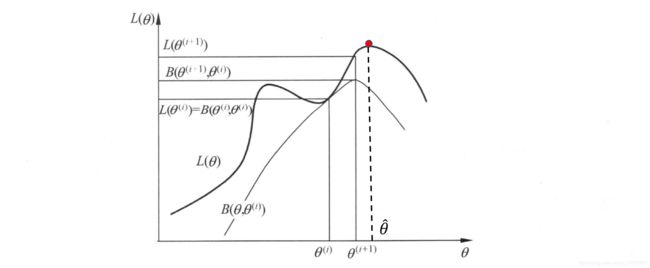
通过上图可知,在每一步迭代中,先固定 θ i \theta_i θi确保似然函数改变参数后依旧增长,调整 θ ( i + 1 ) \theta^{(i+1)} θ(i+1)使得下界取到极值,下一次迭代中,固定 θ ( i + 1 ) \theta^{(i+1)} θ(i+1),寻找下一个参数使得下界取到极值,循环往复,直到收敛到最优值 θ ^ \hat{\theta} θ^。但是也可以看出EM算法不能保证找到全局最优值。
9.2 EM算法的收敛性
定理9.1

这个定理表明,EM算法每次迭代求得最大化完全数据模型似然函数的参数 θ \theta θ会使观测数据的似然函数增大,这是一个很好的性质,因为最终目的就是使得观测数据似然函数最大。
定理9.2(收敛性的说明——局部最优)

表明EM的收敛性包含关于对数似然函数序列的收敛性与关于参数估计序列的收敛性两层意思;且参数估计序列收敛到对数似然函数序列的稳定点,不能保证收敛到极大值点,所以EM算法会收敛到局部的最大值。因此:初值的选择相对重要,可尝试不同初值带入,并加以比较。
- 若 L ( θ , θ ( i ) ) L(\theta,\theta^{(i)}) L(θ,θ(i))是凸函数,则可以收敛到全局最大值,这点和梯度下降算法相似。
9.3 EM算法在高斯混合模型学习下的应用
9.3.1 高斯混合模型GMM
高斯分布就是俗称的正态分布。
高斯混合模型的具体含义(以一维为例):
观测数据Y不来自于同一高斯分布,而是以 α k \alpha_k αk的概率来自于参数 θ k = ( μ k , σ k ) \theta_k=(\mu_k,\sigma _k) θk=(μk,σk)不同的k个高斯分布模型 ϕ ( y ∣ θ k ) \phi (y|\theta_k) ϕ(y∣θk)。在这个过程之中,来自哪个高斯分布是无法观测,因此可以称该变量叫做隐变量,因此适用于EM求解。
定义9.2 高斯混合模型
概率分布模型为:
P ( y ∣ θ ) = ∑ k = 1 K α k ϕ ( y ∣ θ k ) P(y|\theta)=\sum\limits_{k=1}^K\alpha_k\phi (y|\theta_k) P(y∣θ)=k=1∑Kαkϕ(y∣θk)
其中:
α k ⩾ 0 ∑ k = 1 K α k = 1 ϕ ( y ∣ θ k ) = 1 2 π σ k exp ( − ( y − μ k ) 2 2 σ k 2 ) \alpha_k \geqslant 0\\ \sum_{k=1}^K\alpha_k = 1\\ \phi (y|\theta_k) = \frac{1}{\sqrt{2\pi}\sigma_k}\exp(-\frac{(y-\mu_k)^2}{2\sigma_k^2}) αk⩾0k=1∑Kαk=1ϕ(y∣θk)=2πσk1exp(−2σk2(y−μk)2)
类比三硬币模型的形式: P ( Y ∣ θ ) = ∑ Z P ( Z ∣ θ ) P ( Y ∣ Z , θ ) P(Y|\theta)=\sum\limits_ZP(Z|\theta)P(Y|Z,\theta) P(Y∣θ)=Z∑P(Z∣θ)P(Y∣Z,θ)
其中 P ( Z ∣ θ ) P(Z|\theta) P(Z∣θ)看作是 α \alpha α,当参数确定时,为 Z = Z i Z=Z_i Z=Zi的概率; P ( Y ∣ Z , θ ) P(Y|Z,\theta) P(Y∣Z,θ)看作是不同的高斯概率分布,当参数和 Z = Z i Z=Z_i Z=Zi确定时,该分布也确定了。
9.3.2 高斯混合模型参数估计的EM算法
- 确定隐变量,写出完全数据的对数似然函数。
假定观测数据产生如下:
α k , ϕ ( y ∣ θ k ) ⇒ y j \alpha_k,\phi (y|\theta_k)\Rightarrow y_j αk,ϕ(y∣θk)⇒yj
但是 y i y_i yi来自于第k个分模型中的哪一个无法观测,定义隐变量
γ j k = { 1 , 第j个观测来自于第k个分模型 0 , 否 则 j = 1 , 2 , . . . , N ; k = 1 , 2 , . . . , K \gamma_{jk}=\left\{\begin{matrix} 1,\ \ \text{第j个观测来自于第k个分模型}& \\ 0,否则& \end{matrix}\right.\\ j=1,2,...,N;\ \ \ k=1,2,...,K γjk={ 1, 第j个观测来自于第k个分模型0,否则j=1,2,...,N; k=1,2,...,K
例如 y 1 y_1 y1来自于第2个分模型,则隐变量为 γ 1 , 2 = ( 0 , 1 , 0 , . . . , 0 ) \gamma_{1,2}=(0,1,0,...,0) γ1,2=(0,1,0,...,0)
由此得到的完全数据为:
( y i , γ j 1 , γ j 2 . . . , γ j K ) , j = 1 , 2 , . . . , N (y_i,\gamma_{j1},\gamma_{j2}...,\gamma_{jK}) , \ \ j=1,2,...,N (yi,γj1,γj2...,γjK), j=1,2,...,N
由此得到完全函数的对数似然函数:
P ( y , γ ∣ θ ) = ∏ j = 1 N P ( y i , γ j 1 , γ j 2 . . . , γ j K ∣ θ ) = ∏ k = 1 K ∏ j = 1 N [ α k , ϕ ( y ∣ θ k ) ] γ j k 令 n k = ∑ j = 1 N γ j k 表 示 来 自 k 分 模 型 中 样 本 的 个 数 , ∑ k = 1 K n k = N = ∏ k = 1 K α k n k ∏ j = 1 N [ ϕ ( y ∣ θ k ) ] γ j k = ∏ k = 1 K α k n k ∏ j = 1 N [ 1 2 π σ k exp ( − ( y − μ k ) 2 2 σ k 2 ) ] r j k P(y,\gamma|\theta) = \prod_{j=1}^NP(y_i,\gamma_{j1},\gamma_{j2}...,\gamma_{jK}|\theta)\\ =\prod_{k=1}^{K}\prod_{j=1}^N\left [ \alpha_k,\phi (y|\theta_k)\right ]^{\gamma_{jk}}\\ 令n_k=\sum\limits_{j=1}^N\gamma_{jk}表示来自k分模型中样本的个数,\ \sum_{k=1}^Kn_k=N\\ = \prod_{k=1}^K \alpha_k^{n_k}\prod\limits_{j=1}^N\left [\phi (y|\theta_k)\right ]^{\gamma_{jk}}\\ =\prod_{k=1}^K \alpha_k^{n_k}\prod\limits_{j=1}^N\left[ \frac{1}{\sqrt{2\pi}\sigma_k}\exp(-\frac{(y-\mu_k)^2}{2\sigma_k^2})\right]^{r_{jk}} P(y,γ∣θ)=j=1∏NP(yi,γj1,γj2...,γjK∣θ)=k=1∏Kj=1∏N[αk,ϕ(y∣θk)]γjk令nk=j=1∑Nγjk表示来自k分模型中样本的个数, k=1∑Knk=N=k=1∏Kαknkj=1∏N[ϕ(y∣θk)]γjk=k=1∏Kαknkj=1∏N[2πσk1exp(−2σk2(y−μk)2)]rjk
取对数,得对数似然函数:
log P ( y , γ ∣ θ ) = { ∑ k = 1 K n k log α k + ∑ j = 1 N r j k [ log ( 1 2 π ) − log σ k − 1 2 σ k 2 ( y j − μ k ) 2 ] } \log P(y,\gamma|\theta) = \begin{Bmatrix} \sum_{k=1}^Kn_k\log\alpha_k+\sum_{j=1}^Nr_{jk}[ \log(\frac{1}{\sqrt{2\pi}})-\log\sigma_k-\frac{1}{2\sigma_k^2}(y_j-\mu_k)^2] \end{Bmatrix} logP(y,γ∣θ)={ ∑k=1Knklogαk+∑j=1Nrjk[log(2π1)−logσk−2σk21(yj−μk)2]}
2.E步:确定Q函数
Q ( θ , θ ( i ) ) = E r j k [ log P ( y , γ ∣ θ ) ∣ y , θ ( i ) ] = E r j k { ∑ k = 1 K n k log α k + ∑ j = 1 N r j k [ log ( 1 2 π ) − log σ k − 1 2 σ k 2 ( y j − μ k ) 2 ] } 用 E ( r j k ) 取 代 r j k = ∑ k = 1 K { ∑ j = 1 N ( E ( r j k ) ) log α k + ∑ j = 1 N E ( r j k ) [ log ( 1 2 π ) − log σ k − 1 2 σ k 2 ( y j − μ k ) 2 ] } Q(\theta,\theta^{(i)})=E_{r_{jk}}[\log P(y,\gamma|\theta)|y,\theta^{(i)}]\\ =E_{r_{jk}}\begin{Bmatrix} \sum_{k=1}^Kn_k\log\alpha_k+\sum_{j=1}^Nr_{jk}[ \log(\frac{1}{\sqrt{2\pi}})-\log\sigma_k-\frac{1}{2\sigma_k^2}(y_j-\mu_k)^2] \end{Bmatrix}\\ \text{} \\ \text用E(r_{jk})取代r_{jk}\\ \\ = \sum_{k=1}^K\begin{Bmatrix} \sum_{j=1}^N(E(r_{jk}))\log\alpha_k+\sum_{j=1}^NE(r_{jk})[ \log(\frac{1}{\sqrt{2\pi}})-\log\sigma_k-\frac{1}{2\sigma_k^2}(y_j-\mu_k)^2]\end{Bmatrix} Q(θ,θ(i))=Erjk[logP(y,γ∣θ)∣y,θ(i)]=Erjk{ ∑k=1Knklogαk+∑j=1Nrjk[log(2π1)−logσk−2σk21(yj−μk)2]}用E(rjk)取代rjk=k=1∑K{ ∑j=1N(E(rjk))logαk+∑j=1NE(rjk)[log(2π1)−logσk−2σk21(yj−μk)2]}
这里涉及到 E ( r j k ∣ y , θ ) E(r_{jk}|y,\theta) E(rjk∣y,θ)得求解:
γ j k ^ = E ( r j k ∣ y , θ ) = P ( γ j k = 1 ∣ y , θ ) = P ( γ j k = 1 , y j ∣ θ ) ∑ k = 1 K P ( γ j k = 1 , y j ∣ θ ) = P ( y j ∣ γ j k = 1 , θ ) P ( γ j k = 1 ∣ θ ) ∑ k = 1 K P ( y j ∣ γ j k = 1 , θ ) P ( γ j k = 1 ∣ θ ) = α k ϕ ( y ∣ θ k ) ∑ k = 1 K α k ϕ ( y ∣ θ k ) \hat{\gamma_{jk}}=E({r_{jk}}|y,\theta)=P(\gamma_{jk}=1|y,\theta)\\ = \frac{P(\gamma_{jk}=1,y_j|\theta)}{\sum_{k=1}^KP(\gamma_{jk}=1,y_j|\theta)}\\ =\frac {P(y_j|\gamma_{jk}=1,\theta)\color{Red}P(\gamma_{jk}=1|\theta)}{\sum_{k=1}^KP(y_j|\gamma_{jk}=1,\theta){\color{Red}P(\gamma_{jk}=1|\theta)}}\\ =\frac{ \alpha_k\phi (y|\theta_k)}{\sum_{k=1}^K\alpha_k\phi (y|\theta_k)} γjk^=E(rjk∣y,θ)=P(γjk=1∣y,θ)=∑k=1KP(γjk=1,yj∣θ)P(γjk=1,yj∣θ)=∑k=1KP(yj∣γjk=1,θ)P(γjk=1∣θ)P(yj∣γjk=1,θ)P(γjk=1∣θ)=∑k=1Kαkϕ(y∣θk)αkϕ(y∣θk)
这里称 γ j k ^ \hat{\gamma_{jk}} γjk^是当前模型参数下第j个观测数据来自第k个分模型的概率,称为分模型对观测数据 y j y_j yj得响应度。
将得到的 E γ j k E_{\gamma_{jk}} Eγjk带入Q函数中(带入过程中 n k n_k nk也相应的变成 ∑ j = 1 N E ( r j k ) \sum_{j=1}^NE(r_{jk}) ∑j=1NE(rjk)),得到:
Q ( θ , θ ( i ) ) = ∑ k = 1 K { n k log α k + ∑ j = 1 N γ j k ^ [ log ( 1 2 π ) − log σ k − 1 2 σ k 2 ( y j − μ k ) 2 ] } Q(\theta,\theta^{(i)})=\sum_{k=1}^K\begin{Bmatrix} {\color{Red}n_k}\log\alpha_k+\sum_{j=1}^N{\color{Red}\hat{\gamma_{jk}}}[ \log(\frac{1}{\sqrt{2\pi}})-\log\sigma_k-\frac{1}{2\sigma_k^2}(y_j-\mu_k)^2]\end{Bmatrix} Q(θ,θ(i))=k=1∑K{ nklogαk+∑j=1Nγjk^[log(2π1)−logσk−2σk21(yj−μk)2]}
- M步:极大化Q函数
求函数Q对 θ \theta θ的最大值作为新一轮迭代模型的参数:
θ ( i + 1 ) = arg max Q ( θ , θ ( i ) ) \theta^{(i+1)}=\arg\max Q(\theta,\theta^{(i)}) θ(i+1)=argmaxQ(θ,θ(i))
模型参数 θ ( i + 1 ) \theta^{(i+1)} θ(i+1)包括 ( α k , μ k , σ k 2 ) (\alpha_k,\mu_k,\sigma_k^2) (αk,μk,σk2),通过极大似然估计分别对 α k , μ k , σ k 2 \alpha_k,\mu_k,\sigma_k^2 αk,μk,σk2求偏导数令其为0,其中 α k ^ \hat{\alpha_k} αk^是在 ∑ k = 1 K α k = 1 \sum_{k=1}^K\alpha_k=1 ∑k=1Kαk=1限制条件下求解的。通过该过程求得的解如下:
μ k ^ = ∑ j = 1 N γ j k ^ y j ∑ j = 1 N γ j k ^ σ k 2 = ∑ j = 1 N γ j k ^ ( y j − μ k ) 2 ∑ j = 1 N γ j k ^ α k = n k N = ∑ j = 1 N γ j k ^ N \hat{\mu_k}=\frac{\sum_{j=1}^N\hat{\gamma_{jk}}y_j}{\sum_{j=1}^N\hat{\gamma_{jk}}} \ \ \sigma_k^2=\frac{\sum_{j=1}^N\hat{\gamma_{jk}}(y_j-\mu_k)^2}{\sum_{j=1}^N\hat{\gamma_{jk}}} \ \ \alpha_k=\frac{n_k}{N}=\frac{\sum_{j=1}^N\hat{\gamma_{jk}}}{N} μk^=∑j=1Nγjk^∑j=1Nγjk^yj σk2=∑j=1Nγjk^∑j=1Nγjk^(yj−μk)2 αk=Nnk=N∑j=1Nγjk^
到此一次EM迭代结束,重复以上步骤,直到实现停止条件(对数似然函数不明显变化或参数不明显变化。
算法9.2 高斯混合模型参数估计的EM算法
输入:观测数据Y,高斯混合模型;
输出:高斯混合模型参数。
(1)去参数的初始值开始迭代(由于EM算法对初始值敏感,可以通过赋值不同的初始值比较模型)
(2)E步,根据当前的模型参数,计算分模型k对观测数据的响应度。
γ j k ^ = α k ϕ ( y ∣ θ k ) ∑ k = 1 K α k ϕ ( y ∣ θ k ) j = 1 , 2 , . . . , N ; k = 1 , 2 , . . . K \hat{\gamma_{jk}} = \frac{ \alpha_k\phi (y|\theta_k)}{\sum_{k=1}^K\alpha_k\phi (y|\theta_k)}\ \ j=1,2,...,N;\ \ k=1,2,...K γjk^=∑k=1Kαkϕ(y∣θk)αkϕ(y∣θk) j=1,2,...,N; k=1,2,...K
(3)计算新一轮的迭代模型参数 θ \theta θ:
μ k ^ = ∑ j = 1 N γ j k ^ y j ∑ j = 1 N γ j k ^ σ k 2 = ∑ j = 1 N γ j k ^ ( y j − μ k ) 2 ∑ j = 1 N γ j k ^ α k = n k N = ∑ j = 1 N γ j k ^ N \hat{\mu_k}=\frac{\sum_{j=1}^N\hat{\gamma_{jk}}y_j}{\sum_{j=1}^N\hat{\gamma_{jk}}} \ \ \sigma_k^2=\frac{\sum_{j=1}^N\hat{\gamma_{jk}}(y_j-\mu_k)^2}{\sum_{j=1}^N\hat{\gamma_{jk}}} \ \ \alpha_k=\frac{n_k}{N}=\frac{\sum_{j=1}^N\hat{\gamma_{jk}}}{N} μk^=∑j=1Nγjk^∑j=1Nγjk^yj σk2=∑j=1Nγjk^∑j=1Nγjk^(yj−μk)2 αk=Nnk=N∑j=1Nγjk^
(4)重复(2)(3)直到收敛。
9.4 EM算法的推广
EM算法的另外一种解释(F函数)与应用(GEM)。
首先通过图形的方式理解EM的算法原理。
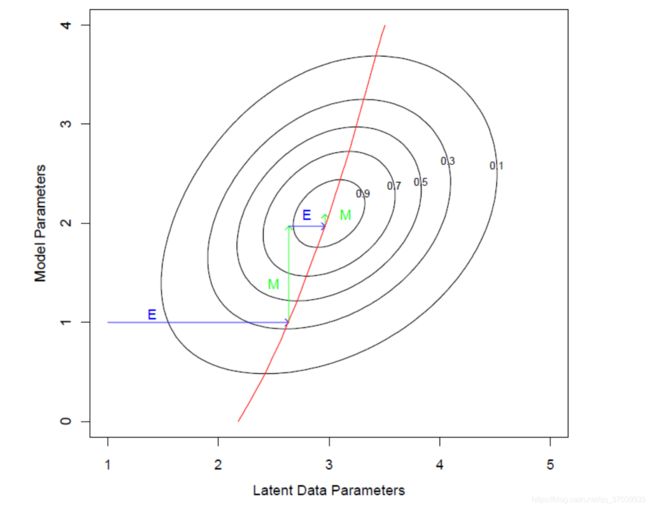
图引自《The Elements of Statistical Learning》
红色曲线为 P ( Z ∣ Y , θ ) P(Z|Y,\theta) P(Z∣Y,θ),横坐标为隐变量,纵坐标为模型参数,等高线可以理解为Q函数或F函数,如图所示,EM算法可以理解,E步为了寻找最优的隐变量分布(即红色线上的点),M步为了寻找在当前隐变量分布下,使得Q函数或F函数极大的模型参数,并不断迭代,最终至收敛。
9.4.1 F F F函数的极大-极大算法
F函数:假设隐变量数据Z的概率分布为 P ~ ( Z ) {\tilde{P}(Z)} P~(Z),定义分布 P ~ \tilde{P} P~与参数 θ \theta θ的函数 F ( P ~ , θ ) F(\tilde{P},\theta) F(P~,θ):
F ( P ~ , θ ) = E P ~ [ log P ( Y , Z ∣ θ ) ] + H ( P ~ ) F(\tilde{P},\theta) =E_{\tilde{P}}[\log P(Y,Z|\theta)]\ +\ H(\tilde{P}) F(P~,θ)=EP~[logP(Y,Z∣θ)] + H(P~)
其中 H ( P ~ ) = − E P ~ log P ~ ( Z ) H(\tilde{P})=-E_{\tilde{P}}\log\tilde{P}(Z) H(P~)=−EP~logP~(Z),是分布 P ~ ( Z ) {\tilde{P}(Z)} P~(Z)的熵。
EM函数中分别通过E和M步骤求解隐函数分布和参数,而F函数将这两个步骤融合在一个函数中,通过固定其一,调整另一个的策略完成求解。
- 第一个极大:固定 θ \theta θ,关于Z的分布求F极大值:

证明:
拉格朗日方法求解关于 P ~ ( Z ) {\tilde{P}(Z)} P~(Z)的极大值问题:
L = E P ~ [ log P ( Y , Z ∣ θ ) ] − E P ~ log P ~ ( Z ) + λ [ 1 − ∑ Z P ~ ( Z ) ] L=E_{\tilde{P}}[\log P(Y,Z|\theta)]\ -E_{\tilde{P}}\log\tilde{P}(Z) +\lambda[1-\sum_Z\tilde{P}(Z)] L=EP~[logP(Y,Z∣θ)] −EP~logP~(Z)+λ[1−Z∑P~(Z)]
其中 ∑ z P ~ ( Z ) = 1 \sum_z\tilde{P}(Z)=1 ∑zP~(Z)=1为约束条件。
将其对 P ~ ( Z ) \tilde{P}(Z) P~(Z)求导并令导数等于0求得:
λ = log P ( Y , Z ∣ θ ) − log P θ ~ ( Z ) + 1 \lambda=\log P(Y,Z|\theta) - \log\tilde{P_\theta}(Z)+1 λ=logP(Y,Z∣θ)−logPθ~(Z)+1
变换该式子得:
P ( Y , Z ∣ θ ) P θ ~ ( Z ) = e λ + 1 \frac{P(Y,Z|\theta)}{\tilde{P_\theta}(Z)}=e^{\lambda+1} Pθ~(Z)P(Y,Z∣θ)=eλ+1
通过该式子可以得知,因为 P ( Y , Z ∣ θ ) P(Y,Z|\theta) P(Y,Z∣θ)是连续的,所以 P θ ~ ( Z ) \tilde{P_\theta}(Z) Pθ~(Z)也随 θ \theta θ连续变化。
又因为 ∑ z P ~ ( Z ) = 1 \sum_z\tilde{P}(Z)=1 ∑zP~(Z)=1,所以可以得出:
P ~ θ ( Z ) = P ( Z ∣ Y , θ ) \tilde{P}_\theta(Z)=P(Z|Y,\theta) P~θ(Z)=P(Z∣Y,θ)
这个性质确保了第一个极大步骤的可行性,固定 θ \theta θ,寻找最佳的隐变量分布时,目的是使得当前的 F θ ( P ~ , θ ) F_\theta(\tilde{P},\theta) Fθ(P~,θ)最大。该性质表明,通过该方式寻找到的最佳隐变量唯一且正好取在 P ( Z ∣ Y , θ ) {P(Z|Y,\theta)} P(Z∣Y,θ)这个点上,结果很理想。 - 第二个极大:固定 P ~ ( Z ) {\tilde{P}(Z)} P~(Z),关于 θ \theta θ求F极大值。
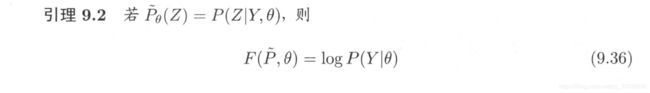
证明:
F ( P ~ , θ ) = E P ~ [ log P ( Y , Z ∣ θ ) ] + H ( P ~ ) = E P ~ [ log P ( Y , Z ∣ θ ) ] − E P ~ log P ~ ( Z ) = P ~ θ ( Z ) ∑ Z log P ( Y , Z ∣ θ ) − P ~ ( Z ) ∑ Z log P ~ ( Z ) 若 P ~ θ ( Z ) = P ( Z ∣ Y , θ ) , 带 入 上 式 = P ( Z ∣ Y , θ ) ∑ Z log P ( Y , Z ∣ θ ) − P ( Z ∣ Y , θ ) ∑ Z log P ( Z ∣ Y , θ ) = [ log P ( Y , Z ∣ θ ) − log P ( Z ∣ Y , θ ) ] ∑ Z P ( Z ∣ Y , θ ) = [ log P ( Y , Z ∣ θ ) P ( Z ∣ Y , θ ) ] ∑ Z P ( Z ∣ Y , θ ) = log P ( Y ∣ θ ) ∑ Z P ( Z ∣ Y , θ ) 因 为 ∑ Z P ( Z ∣ Y , θ ) = 1 = log P ( Y ∣ θ ) F(\tilde{P},\theta)=E_{\tilde{P}}[\log P(Y,Z|\theta)]\ +\ H(\tilde{P}) \\=E_{\tilde{P}}[\log P(Y,Z|\theta)]\ -E_{\tilde{P}}\log\tilde{P}(Z)\\ =\tilde{P}_\theta(Z)\sum_Z\log P(Y,Z|\theta)\ -\tilde{P}(Z)\sum_Z\log\tilde{P}(Z)\\ 若\tilde{P}_\theta(Z)=P(Z|Y,\theta),带入上式\\=P(Z|Y,\theta)\sum_Z\log P(Y,Z|\theta)\ -P(Z|Y,\theta)\sum_Z\log P(Z|Y,\theta)\\=[\log P(Y,Z|\theta)\ - \log P(Z|Y,\theta)]\sum_ZP(Z|Y,\theta)\\=[\log \frac {P(Y,Z|\theta)}{P(Z|Y,\theta)}]\sum_ZP(Z|Y,\theta)\\=\log P(Y|\theta)\sum_ZP(Z|Y,\theta)\\因为\sum_ZP(Z|Y,\theta)=1\\=\log P(Y|\theta) F(P~,θ)=EP~[logP(Y,Z∣θ)] + H(P~)=EP~[logP(Y,Z∣θ)] −EP~logP~(Z)=P~θ(Z)Z∑logP(Y,Z∣θ) −P~(Z)Z∑logP~(Z)若P~θ(Z)=P(Z∣Y,θ),带入上式=P(Z∣Y,θ)Z∑logP(Y,Z∣θ) −P(Z∣Y,θ)Z∑logP(Z∣Y,θ)=[logP(Y,Z∣θ) −logP(Z∣Y,θ)]Z∑P(Z∣Y,θ)=[logP(Z∣Y,θ)P(Y,Z∣θ)]Z∑P(Z∣Y,θ)=logP(Y∣θ)Z∑P(Z∣Y,θ)因为Z∑P(Z∣Y,θ)=1=logP(Y∣θ)
这个性质表明:当我们把 P ~ θ ( Z ) \tilde{P}_\theta(Z) P~θ(Z)设为 P ( Z ∣ Y , θ ) P(Z|Y,\theta) P(Z∣Y,θ)时,恰好目标函数 log P ( Y ∣ θ ) \log P(Y|\theta) logP(Y∣θ)等于F函数,而且去除了隐变量,这为第二个极大提供了保证,关于 θ \theta θ求极大。
这步正是EM算法要解决的问题,该步骤等价于EM中的:
θ = arg max θ log P ( Y ∣ θ ) \theta = \arg\max_\theta\log P(Y|\theta) θ=argθmaxlogP(Y∣θ)
通过以上两个极大步骤的迭代求得得 P ~ ∗ , θ ∗ \tilde{P}^*,\theta^* P~∗,θ∗与EM算法的关系
 这个性质说明了,两个方法求得的最优解相同。
这个性质说明了,两个方法求得的最优解相同。
通过该算法得知,F函数的极大-极大算法求得的参数估计序列与EM算法求得的参数估计序列相同,很好的解释了EM算法。
9.4.2 GEM算法
GEM:广义EM算法。
算法9.3 GEM算法1
输入:观测数据,F函数;
输出:模型参数。
(1)初始化参数 θ ( 0 ) \theta^{(0)} θ(0),开始迭代;
(2)第(i+1)次迭代:
第一步:记 θ ( i ) \theta^{(i)} θ(i)为参数 θ \theta θ的估计值, P ~ ( i ) \tilde{P}^{(i)} P~(i)为函数 P ~ \tilde{P} P~的估计,求 P ~ ( i + 1 ) \tilde{P}^{(i+1)} P~(i+1)使 P ~ \tilde{P} P~极大化 F ( P ~ , θ ( i ) ) F(\tilde{P},\theta^{(i)}) F(P~,θ(i));
第二步:求 θ ( i + 1 ) \theta^{(i+1)} θ(i+1)使得 F ( P ~ ( i + 1 ) , θ ) F(\tilde{P}^{(i+1)},\theta) F(P~(i+1),θ)极大化。
(3)重复(2)的迭代,直到收敛。
GEM算法1中有时 Q ( θ , θ ( i ) ) Q(\theta,\theta^{(i)}) Q(θ,θ(i))(或 F ( P ~ ( i + 1 ) , θ ) F(\tilde{P}^{(i+1)},\theta) F(P~(i+1),θ))过于复杂,直接求它的极大化很困难。GEM算法2和GEM算法3为了解决这个问题,不直接求使得Q函数达到极大的 θ ( i + 1 ) \theta^{(i+1)} θ(i+1),而是找一个 θ ( i + 1 ) \theta^{(i+1)} θ(i+1)使得 Q ( θ ( i + 1 ) , ( θ ( i ) ) > Q ( ( θ ( i ) , ( θ ( i ) ) Q(\theta^{(i+1)},(\theta^{(i)})>Q((\theta^{(i)},(\theta^{(i)}) Q(θ(i+1),(θ(i))>Q((θ(i),(θ(i))
算法9.4 GEM算法2(模型参数维数为1维)
输入:观测数据,Q函数;
输出:模型参数。
(1)初始化参数 θ ( 0 ) \theta^{(0)} θ(0),开始迭代;
(2)第(i+1)次迭代:
第一步:记 θ ( i ) \theta^{(i)} θ(i)为参数 θ \theta θ的估计值,计算:
Q ( θ , θ ( i ) ) = E Z [ log ( P ( Y , Z ∣ θ ) ∣ Y , θ ( i ) ] = ∑ Z log ( P ( Y , Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) Q(\theta,\theta^{(i)})=E_Z\left [ \log(P(Y,Z|\theta)|Y,\theta^{(i)} \right]\\ = \sum_Z\log(P(Y,Z|\theta)P(Z|Y,\theta^{(i)}) Q(θ,θ(i))=EZ[log(P(Y,Z∣θ)∣Y,θ(i)]=Z∑log(P(Y,Z∣θ)P(Z∣Y,θ(i))
第二步:求 θ ( i + 1 ) \theta^{(i+1)} θ(i+1)使得
Q ( θ ( i + 1 ) , ( θ ( i ) ) > Q ( ( θ ( i ) , ( θ ( i ) ) Q(\theta^{(i+1)},(\theta^{(i)})>Q((\theta^{(i)},(\theta^{(i)}) Q(θ(i+1),(θ(i))>Q((θ(i),(θ(i))
(3)重复(2)的迭代,直到收敛。
算法9.5 GEM算法3(模型参数维数为d维,d>=2)
基本思想:将EM算法的M步分解为d次条件极大化,每次只改变参数向量的一个分量,其余分量不变。
输入:观测数据,Q函数;
输出:模型参数。
(1)初始化参数 θ ( 0 ) = ( θ 1 ( 0 ) , θ 2 ( 0 ) , . . . , θ d ( 0 ) ) \theta^{(0)}=(\theta_1^{(0)},\theta_2^{(0)},...,\theta_d^{(0)}) θ(0)=(θ1(0),θ2(0),...,θd(0)),开始迭代;
(2)第(i+1)次迭代:
- 第一步:记 θ ( i ) = ( θ 1 ( i ) , θ 2 ( i ) , . . . , θ d ( i ) ) \theta^{(i)}=(\theta_1^{(i)},\theta_2^{(i)},...,\theta_d^{(i)}) θ(i)=(θ1(i),θ2(i),...,θd(i))为参数 θ \theta θ的估计值,计算:
Q ( θ , θ ( i ) ) = E Z [ log ( P ( Y , Z ∣ θ ) ∣ Y , θ ( i ) ] = ∑ Z log ( P ( Y , Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) Q(\theta,\theta^{(i)})=E_Z\left [ \log(P(Y,Z|\theta)|Y,\theta^{(i)} \right]\\ = \sum_Z\log(P(Y,Z|\theta)P(Z|Y,\theta^{(i)}) Q(θ,θ(i))=EZ[log(P(Y,Z∣θ)∣Y,θ(i)]=Z∑log(P(Y,Z∣θ)P(Z∣Y,θ(i)) - 第二步:进行d次条件极大化
首先,在 θ 2 ( i ) , θ 3 ( i ) , . . . , θ d ( i ) \theta_2^{(i)},\theta_3^{(i)},...,\theta_d^{(i)} θ2(i),θ3(i),...,θd(i)保持不变的条件下求使Q函数达到极大的 θ 1 ( i + 1 ) \theta_1^{(i+1)} θ1(i+1);
然后在 θ 1 = θ 1 ( i + 1 ) , θ j = θ j ( i ) , j = 3 , 4 , . . . d \theta_1=\theta_1^{(i+1)},\theta_j=\theta_j^{(i)},j=3,4,...d θ1=θ1(i+1),θj=θj(i),j=3,4,...d的条件下求使Q函数达到极大的 θ 2 ( i + 1 ) \theta_2^{(i+1)} θ2(i+1);
以此类推,经过d次条件极大化,得到 θ ( i + 1 ) = ( θ 1 ( i + 1 ) , θ 2 ( i + 1 ) , . . . , θ d ( i + 1 ) ) \theta^{(i+1)}=(\theta_1^{(i+1)},\theta_2^{(i+1)},...,\theta_d^{(i+1)}) θ(i+1)=(θ1(i+1),θ2(i+1),...,θd(i+1))
Q ( θ ( i + 1 ) , ( θ ( i ) ) > Q ( ( θ ( i ) , ( θ ( i ) ) Q(\theta^{(i+1)},(\theta^{(i)})>Q((\theta^{(i)},(\theta^{(i)}) Q(θ(i+1),(θ(i))>Q((θ(i),(θ(i))
(3)重复(2)的迭代,直到收敛。
习题9.1python实现
def cal_u(pi, p, q, xi):
"""
u值计算
:param pi: 下一次迭代开始的 pi
:param p: 下一次迭代开始的 p
:param q: 下一次迭代开始的 q
:param xi: 观察数据第i个值,从0开始
:return:
"""
return pi * math.pow(p, xi) * math.pow(1 - p, 1 - xi) / \
float(pi * math.pow(p, xi) * math.pow(1 - p, 1 - xi) +
(1 - pi) * math.pow(q, xi) * math.pow(1 - q, 1 - xi))
def e_step(pi,p,q,x):
"""
e步计算
:param pi: 下一次迭代开始的 pi
:param p: 下一次迭代开始的 p
:param q: 下一次迭代开始的 q
:param x: 观察数据
:return:
"""
return [cal_u(pi,p,q,xi) for xi in x]
def m_step(u,x):
"""
m步计算
:param u: m步计算的u
:param x: 观察数据
:return:
"""
pi1=sum(u)/len(u)
p1=sum([u[i]*x[i] for i in range(len(u))]) / sum(u)
q1=sum([(1-u[i])*x[i] for i in range(len(u))]) / sum([1-u[i] for i in range(len(u))])
return [pi1,p1,q1]
终止条件:
def run(observed_x, start_pi, start_p, start_q, iter_num):
"""
:param observed_x: 观察数据
:param start_pi: 下一次迭代开始的pi $\pi$
:param start_p: 下一次迭代开始的p
:param start_q: 下一次迭代开始的q
:param iter_num: 迭代次数
:return:
"""
for i in range(iter_num):
u = e_step(start_pi, start_p, start_q, observed_x)
print (i,[start_pi,start_p,start_q])
if [start_pi,start_p,start_q]== m_step(u, observed_x):#收敛条件
break
else:
[start_pi,start_p,start_q]= m_step(u, observed_x)
调用:
# 观察数据
x = [1, 1, 0, 1, 0, 0, 1, 0, 1, 1]
# 初始化 pi,p q
[pi, p, q] = [0.45, 0.55, 0.67]
# 迭代计算
run(x,pi,p,q,100)
习题9.2
证明引理9.2
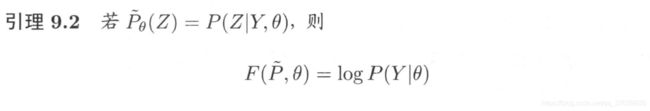
证明:
F ( P ~ , θ ) = E P ~ [ log P ( Y , Z ∣ θ ) ] + H ( P ~ ) = E P ~ [ log P ( Y , Z ∣ θ ) ] − E P ~ log P ~ ( Z ) = P ~ θ ( Z ) ∑ Z log P ( Y , Z ∣ θ ) − P ~ ( Z ) ∑ Z log P ~ ( Z ) 若 P ~ θ ( Z ) = P ( Z ∣ Y , θ ) , 带 入 上 式 = P ( Z ∣ Y , θ ) ∑ Z log P ( Y , Z ∣ θ ) − P ( Z ∣ Y , θ ) ∑ Z log P ( Z ∣ Y , θ ) = [ log P ( Y , Z ∣ θ ) − log P ( Z ∣ Y , θ ) ] ∑ Z P ( Z ∣ Y , θ ) = [ log P ( Y , Z ∣ θ ) P ( Z ∣ Y , θ ) ] ∑ Z P ( Z ∣ Y , θ ) = log P ( Y ∣ θ ) ∑ Z P ( Z ∣ Y , θ ) 因 为 ∑ Z P ( Z ∣ Y , θ ) = 1 = log P ( Y ∣ θ ) F(\tilde{P},\theta)=E_{\tilde{P}}[\log P(Y,Z|\theta)]\ +\ H(\tilde{P}) \\=E_{\tilde{P}}[\log P(Y,Z|\theta)]\ -E_{\tilde{P}}\log\tilde{P}(Z)\\ =\tilde{P}_\theta(Z)\sum_Z\log P(Y,Z|\theta)\ -\tilde{P}(Z)\sum_Z\log\tilde{P}(Z)\\ 若\tilde{P}_\theta(Z)=P(Z|Y,\theta),带入上式\\=P(Z|Y,\theta)\sum_Z\log P(Y,Z|\theta)\ -P(Z|Y,\theta)\sum_Z\log P(Z|Y,\theta)\\=[\log P(Y,Z|\theta)\ - \log P(Z|Y,\theta)]\sum_ZP(Z|Y,\theta)\\=[\log \frac {P(Y,Z|\theta)}{P(Z|Y,\theta)}]\sum_ZP(Z|Y,\theta)\\=\log P(Y|\theta)\sum_ZP(Z|Y,\theta)\\因为\sum_ZP(Z|Y,\theta)=1\\=\log P(Y|\theta) F(P~,θ)=EP~[logP(Y,Z∣θ)] + H(P~)=EP~[logP(Y,Z∣θ)] −EP~logP~(Z)=P~θ(Z)Z∑logP(Y,Z∣θ) −P~(Z)Z∑logP~(Z)若P~θ(Z)=P(Z∣Y,θ),带入上式=P(Z∣Y,θ)Z∑logP(Y,Z∣θ) −P(Z∣Y,θ)Z∑logP(Z∣Y,θ)=[logP(Y,Z∣θ) −logP(Z∣Y,θ)]Z∑P(Z∣Y,θ)=[logP(Z∣Y,θ)P(Y,Z∣θ)]Z∑P(Z∣Y,θ)=logP(Y∣θ)Z∑P(Z∣Y,θ)因为Z∑P(Z∣Y,θ)=1=logP(Y∣θ)
习题9.3 python实现
import numpy as np
from scipy.stats import norm
y = np.array([-67, -48, 6, 8, 14, 16, 23, 24, 28, 29, 41, 49, 56, 60, 75])
K = 2 # 分模型数
N = 15 # 观测值个数
# 参数初始化
mu = np.array([0.5, 0.5])
sg = np.array([1.0, 1.0]) * 10 #sigma
al = np.array([0.5, 0.5])#alpha
for i in range(10):
gm = np.zeros((N, K))#隐变量gamma矩阵
# E 步
for j in range(N):
for k in range(K):
gm[j, k] = al[k] * norm(mu[k], sg[k]).pdf(y[j]) #计算gamma矩阵
gm[j, :] /= sum(gm[j, :])
# M 步
mu2 = y.dot(gm) / sum(gm)
al2 = sum(gm) / N
sg2 = np.zeros((2,))
sg2[0] = sum(gm[:, 0] * (y - mu[0]) ** 2) / sum(gm[:, 0])
sg2[1] = sum(gm[:, 1] * (y - mu[1]) ** 2) / sum(gm[:, 1])
if sum((mu - mu2) ** 2 + (sg - sg2) ** 2 + (al - al2) ** 2) < 0.01:#设置阈值,参数平方误差和小于0.01
break
mu = mu2
sg = sg2
al = al2
print("迭代次数: ", i + 1, "\n", "mu = ", mu, "\n", "sg = ", sg, "\n", "al = ", al, "\n")
习题9.4 混合贝叶斯模型
首先拓展EM的一般形式:
这里提到的Q和 ω ( i ) \omega^{(i)} ω(i)都指隐函数Z的一种概率分布。
具体的证明过程

按照一般形式,对混合贝叶斯模型进行求解。


参考
[1] 《统计学习导论》李航
[2] 《The Elements of Statistical Learning》
[3] https://blog.csdn.net/weixin_37824195/article/details/61623718
[4] https://www.zhihu.com/question/47830123
[5] https://blog.csdn.net/weiwei19890308/article/details/82943969
[6] https://blog.csdn.net/danerer/article/details/80282798#mixture-of-naive-bayes-model
[7]https://blog.csdn.net/Irving_zhang/article/details/64439131?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-19.nonecase&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-19.nonecase
笔者刚刚入门学习机器学习,因为水平有限,李航老师的书对入门不是特别友好,还在生啃阶段,如果有错误还请之处。