leetcode 105. 从前序与中序遍历序列构造二叉树

思路分析:
二叉树相关的很多问题的解决思路都有分治法的思想在里面。我们复习一下分治法的思想：把原问题拆解成若干个与原问题结构相同但规模更小的子问题，待子问题解决以后，原问题就得以解决

• 抓住“前序遍历的第 1 个元素一定是二叉树的根结点”，不难写出代码。关键还是拿 LeetCode 上面的例子画一个图，思路就很清晰了。
• 前序遍历数组的第 1个数（索引为0）的数一定是二叉树的根结点，于是可以在中序遍历中找这个根结点的索引，然后把“前序遍历数组”和“中序遍历数组”分为两个部分，就分别对应二叉树的左子树和右子树，分别递归完成就可以了。
  
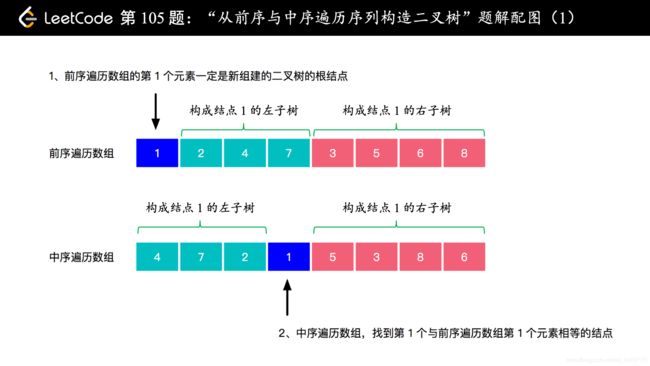
  下面是一个具体的例子，演示了如何计算数组子区间的边界：
  
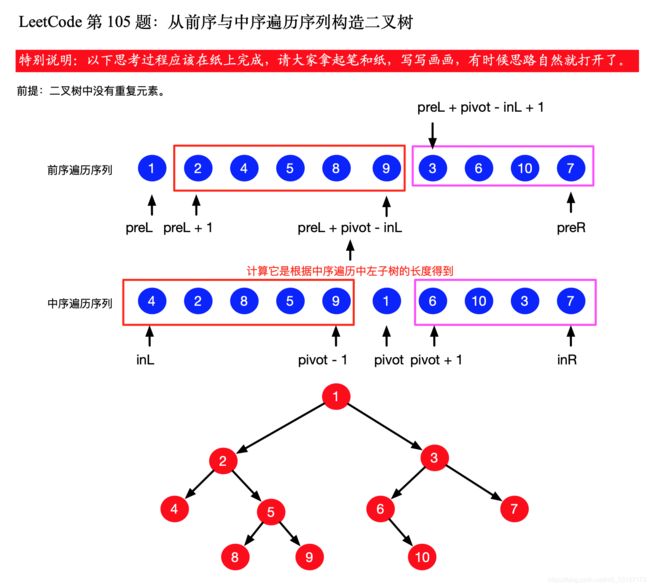
• 建议看完本题可以再看一下中序和后序遍历构造二叉树

leetcode 106. 从中序与后序遍历序列构造二叉树

方法一：在递归方法中，传入数组的拷贝（不推荐、复杂度较高）

class Solution {
     
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
    {
     
        //如果当前数组元素为空，那么为空节点(这里写当前前序数组和当前后序数组都一样)
        if (preorder.size() == 0)
            return NULL;
        //如果当前数组只剩一个元素，说明为叶子节点
        if (preorder.size() == 1)
            return new TreeNode(preorder[0]);
        //构造当前根节点
        TreeNode* root = new TreeNode(preorder[0]);
        //通过pos索引找到中序数组中根的下标位置
        int pos = 0;
        for (int i = 0; i < inorder.size(); i++)
        {
     
            if (inorder[i] == preorder[0])
            {
     
                pos = i;
                break;
            }
        }
        //寻找当前左子树的根----需要将当前前序和中序数组部分的左子树部分打包进两个数组
        //对左子树构成的二叉树，寻找当前二叉树的根
        vector<int> p1(preorder.begin()+1, preorder.begin() + 1+pos);
        vector<int>  i1(inorder.begin(), inorder.begin() + pos);
        root->left = buildTree(p1, i1);

        //与上面同理，只不过变成寻找右子树的根
        vector<int> p2(preorder.begin() + 1+pos, preorder.begin() + preorder.size());
        vector<int>  i2(inorder.begin()+pos+1, inorder.begin() +inorder.size());
        root->right = buildTree(p2, i2);

        //返回当前二叉树的根节点
        return root;
    }
};

方法二：在递归方法中，传入子数组的边界下标

• 边界下标的计算，大家可以参考一开始展示计算边界的图片

class Solution {
     
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
    {
     
        int pSize = preorder.size();
        int iSize = inorder.size();
        return buildTree(preorder, inorder, 0, pSize - 1, 0, iSize - 1);
    }
    //pBegin和pEnd分别是当前前序数组的起点和终点     iBegin和iEnd分别是当前中序数组的起点和终点
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder, int pBegin, int pEnd, int iBegin, int iEnd)
    {
     
        //如果指针错位，说明当前位空节点
        if (pBegin > pEnd || iBegin > iEnd)
            return NULL;
        //构造当前根节点---当前前序数组的起点
        TreeNode* root = new TreeNode(preorder[pBegin]);
        //寻找根节点在当前中序数组的下标位置
        int pos = 0;
        while (preorder[pBegin] != inorder[pos])
            pos++;
        //寻找当前左子树根节点
        root->left = buildTree(preorder, inorder, pBegin + 1, pBegin + pos - iBegin,
            iBegin, pos - 1);
        //寻找当前右子树的根节点
        root->right = buildTree(preorder, inorder, pEnd - iEnd + pos + 1, pEnd,
            pos + 1, iEnd);
        return root;
    }
};

方法三：使用哈希表进行查找优化

• 可以在递归构造前，把中序遍历的值和下标放在哈希表中，就不需要通过遍历得到当前根结点在中序遍历中的位置了。

class Solution {
     
    vector<int> preorder;
    unordered_map<int, int> map;
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
    {
     
        int pSize = preorder.size();
        int iSize = inorder.size();
        this->preorder = preorder;
        for (int i = 0; i < iSize; i++)
            map[inorder[i]] = i;
        return buildTree(0, pSize - 1, 0, iSize - 1);
    }
    //pBegin和pEnd分别是当前前序数组的起点和终点     iBegin和iEnd分别是当前中序数组的起点和终点
    TreeNode* buildTree(int pBegin, int pEnd, int iBegin, int iEnd)
    {
     
        //如果指针错位，说明当前位空节点
        if (pBegin > pEnd || iBegin > iEnd)
            return NULL;
        //构造当前根节点---当前前序数组的起点
        TreeNode* root = new TreeNode(preorder[pBegin]);
        //寻找根节点在当前中序数组的下标位置
        int pos = map[preorder[pBegin]];
        //寻找当前左子树根节点
        root->left = buildTree(pBegin + 1, pBegin + pos - iBegin,
            iBegin, pos - 1);
        //寻找当前右子树的根节点
        root->right = buildTree( pEnd - iEnd + pos + 1, pEnd,
            pos + 1, iEnd);
        return root;
    }
};