SPP
Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition
扩展阅读:SPP(Spatial Pyramid Pooling)详解
SPP
现有的深度卷积神经网络(CNNs)需要一个固定尺寸(如224x224)的输入图像。这种要求是 “人为的”,可能会降低任意大小/尺度的图像或子图像的识别精度。在这项工作中,我们为网络配备了另一种池化策略,即 “空间金字塔池化”,以消除上述要求。新的网络结构,称为SPP-net,可以生成一个固定长度的表示,而不管图像的大小/尺度。金字塔池化对物体变形的影响也很大。有了这些优势,SPP-net在总体上应该可以改善所有基于CNN的图像分类方法。在ImageNet 2012数据集上,我们证明了SPP-net可以提高各种CNN架构的准确性,尽管它们的设计不同。在Pascal VOC 2007和Caltech101数据集上,SPP-net使用单一的全图像表示法,无需微调,就能达到最先进的分类结果。
SPP-net的威力在物体检测中也是很重要的。利用SPP-net,我们只需计算一次整个图像的特征图,然后将任意区域(子图像)的特征集中起来,生成固定长度的表示,用于训练检测器。这种方法避免了重复计算卷积特征。在处理测试图像时,我们的方法比R-CNN方法快24-102倍,同时在Pascal VOC 2007上达到了更好或相当的精度。
在2014年ImageNet大规模视觉识别挑战赛(ILSVRC)中,我们的方法在所有38支队伍中物体检测排名第2,图像分类排名第3。本稿件也介绍了针对本次比赛所做的改进。
1 INTRODUCTION
我们正在见证视觉界快速的、革命性的变化,这主要是由深度卷积神经网络(CNN)[1]和大规模训练数据的可用性引起的[2]。最近,基于深度网络的方法在图像分类[3]、[4]、[5]、[6]、物体检测[7]、[8]、[5]、许多其他识别任务[9]、[10]、[11]、[12],甚至非识别任务中的技术状态上都有了很大的改进。
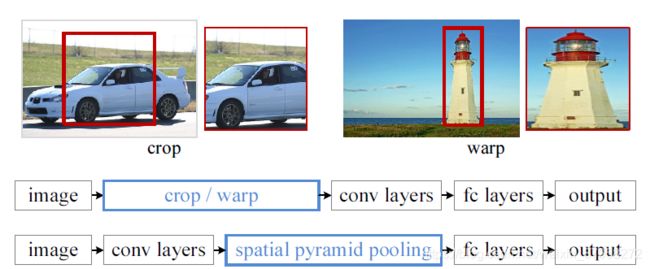
然而,在CNN的训练和测试中存在一个技术问题:目前盛行的CNN需要固定的输入图像尺寸(如224x224),这就限制了输入图像的长宽比和比例。当应用于任意尺寸的图像时,目前的方法大多通过裁剪[3]、[4]或通过扭曲[13]、[7]将输入图像拟合到固定尺寸,如图1(上图)所示。但是裁剪的区域可能不包含整个物体,而扭曲的内容可能会导致不必要的几何变形。识别精度会因为内容丢失或变形而受到影响。此外,当物体的比例变化时,预定义的比例可能不适合。修正输入大小忽略了涉及规模的问题。
那么为什么CNN需要固定的输入大小呢?一个CNN主要由两部分组成:卷积层,以及后面的全连接层。卷积层以滑动窗口的方式运行,并输出表示激活空间排列的特征图(图2)。事实上,卷积层不需要固定的图像尺寸,可以生成任何尺寸的特征图。另一方面,全连接层根据其定义需要有固定尺寸/长度的输入。因此,固定大小的约束只来自于全连接层,它存在于网络的更深阶段。
图1:顶部:裁剪或扭曲以适应固定的尺寸。中间:一个传统的CNN。底部:我们的空间金字塔池化网络结构。
本文引入了一个空间金字塔池化(SPP)[14],[15]层来消除网络的固定大小约束。具体来说,我们在最后一个卷积层的基础上增加一个SPP层。SPP层将特征汇集起来,并产生固定长度的输出,然后将其输入到全连接层(或其他分类器)。换句话说,我们在网络层次结构的更深阶段(卷积层和全连接层之间)进行一些信息 “聚合”,以避免在开始时进行裁剪或扭曲。图1(bottom)显示了引入SPP层后网络结构的变化。我们将新的网络结构称为SPP-net。
空间金字塔池化(Spatial pyramid pooling)[14]、[15](俗称空间金字塔匹配或SPM[15]),作为Bag-of-Words(BoW)模型[16]的扩展,是计算机视觉中最成功的方法之一。它将图像从细到粗的层次划分,并将其中的局部特征聚集起来。在最近CNN盛行之前,SPP早已成为分类(如[17]、[18]、[19])和检测(如[20])的领先和竞赛获奖系统的关键组件。尽管如此,SPP还没有在CNN的背景下被考虑。我们注意到,SPP对于深度CNNs有几个显著的特性。1)SPP能够生成固定长度的输出,而不管输入大小,而之前的深度网络[3]中使用的滑动窗口池化则不能;2)SPP使用multi-level spatial bins,而滑动窗口池化只使用单一窗口大小。 Multi-level pooling已经被证明对物体变形具有鲁棒性[15];3)由于输入尺度的灵活性,SPP可以池化在不同尺度下提取的特征。通过实验我们表明,这些因素都提升了深度网络的识别精度。
SPP-net不仅可以从任意大小的图像/窗口生成表征(representations)进行测试,而且还允许我们在训练过程中输入不同大小或尺度的图像。使用可变尺寸的图像进行训练可以增加尺度不变量,减少过度拟合。我们开发了一种简单的多尺寸训练方法。对于一个单一的网络接受可变的输入尺寸,我们通过多个网络来近似它,这些网络共享所有的参数,而这些网络中的每一个都使用固定的输入尺寸进行训练。在每一个epoch中,我们用一个给定的输入大小来训练网络,并在下一个epoch中切换到另一个输入大小。实验表明,这种多尺寸训练和传统的单尺寸训练一样,可以收敛,并带来更好的测试精度。
SPP的优势与具体的CNN设计是orthogonal的。在ImageNet 2012数据集上进行的一系列控制实验中,我们证明了SPP在现有模型[3]、[4]、[5]中改进了四种不同的CNN架构(或它们的修改),超过了无SPP的对应架构。这些架构有不同的卷积核数量/大小、步长、深度或其他设计。因此,我们有理由推测,SPP应该改善更复杂(更深、更大)的卷积架构。SPP-net还在Caltech101[21]和Pascal VOC 2007[22]上显示了最先进的分类结果,只使用单一的全图像表示,没有进行微调。
SPP-net在物体检测方面也表现出了巨大的优势。在领先的物体检测方法R-CNN[7]中,通过深度卷积网络提取候选窗口的特征。该方法在VOC和ImageNet数据集上都表现出了显著的检测精度。但是RCNN中的特征计算是非常耗时的,因为它要对每幅图像上千个warped regions的原始像素反复应用深度卷积网络。在本文中,我们展示了我们可以在整个图像上只运行一次卷积层(不管窗口的数量),然后在特征图上通过SPP-net提取特征。这种方法比R-CNN的速度提升了一百多倍。需要注意的是,在特征图(而不是图像区域)上训练/运行检测器其实是一个比较流行的想法[23],[24],[20],[5]。但是SPP-net继承了深度CNN特征图的强大功能,同时也继承了SPP在任意窗口大小上的灵活性,从而带来了出色的精度和效率。在我们的实验中,基于SPP-net的系统(建立在R-CNN管道上)计算特征的速度比R-CNN快24-102倍,同时具有更好或相当的精度。通过EdgeBoxes[25]最近的fast proposal method,我们的系统处理一张图像(包括所有步骤)需要0.5秒。这使得我们的方法在实际应用中很实用。
本稿件的初稿已经发表在2014年的ECCV上。基于这项工作,我们参加了ILSVRC 2014[26]的比赛,在所有38支队伍中,物体检测排名第2,图像分类排名第3(均为只提供数据的赛道)。为2014年ILSVRC做了一些修改。我们表明,SPP-网络可以提升各种网络,比无SPP对应的网络更深更大(第3.1.2-3.1.4节)。此外,在我们的检测框架的驱动下,我们发现在具有灵活定位/大小的窗口的特征图上进行多视角测试(Sec.3.1.5)可以提高分类精度。本手稿还提供了这些修改的细节。
2 DEEP NETWORKS WITH SPATIAL PYRAMID POOLING
2.1 Convolutional Layers and Feature Maps
考虑流行的七层架构[3]、[4]。前五层是卷积层,其中一些层之后是池化层。这些池化层也可以被认为是 “卷积”,因为它们使用的是滑动窗口。最后两层是完全连接的,以N-way softmax作为输出,其中N为类别数。
图2:特征图的可视化。(a)Pascal VOC 2007中的两个图像。(b)一些conv5滤波器的特征图。箭头表示最强的responses和它们在图像中的相应位置。©ImageNet图像中相应滤波器的最强响应。绿色的矩形标记了最强响应的感受野。
上面描述的深度网络需要一个固定的图像大小。然而,我们注意到,对固定尺寸的要求只是由于全连接层需要固定长度的向量作为输入。另一方面,卷积层接受任意大小的输入。卷积层使用滑动滤波器,它们的输出与输入具有大致相同的长宽比。这些输出被称为特征图[1]–它们不仅涉及响应的强度,还涉及它们的空间位置。
在图2中,我们将一些特征图可视化。它们是由conv5层的一些卷积核生成的。图2©显示了这些卷积核在ImageNet数据集中最强的激活图像。我们看到一个卷积核可以被一些语义内容激活。例如,55-th卷积核(图2左下角)被一个圆圈形状激活的最多;66-th卷积核(图2右上角)被一个^形状激活的最多;118-th卷积核(图2右下角)被一个v形状激活的最多。输入图像中的这些形状(图2(a))激活了相应位置的特征图(图2中的箭头)
值得注意的是,我们在不固定输入大小的情况下生成图2中的特征图。这些由深度卷积层生成的特征图类似于传统方法[27]、[28]中的特征图。在这些方法中,SIFT向量[29]或图像patcher[28]被densely extracted,然后进行编码,例如,通过向量量化[16]、[15]、[30]、稀疏编码[17]、[18]或Fisher核[19]进行编码。这些编码后的特征由特征图组成,然后由字袋(Bag-of-Words,BoW)[16]或空间金字塔[14],[15]pooled。类似地,深度卷积特征也可以用类似的方式进行池化。
2.2 The Spatial Pyramid Pooling Layer
卷积层接受任意的输入大小,但它们产生的输出是可变大小的。分类器(SVM/softmax)或全连接层需要固定长度的向量。这样的向量可以通过字袋(Bag-of-Words,BoW)方法[16]生成,将特征集中在一起。空间金字塔池化[14],[15]改进了BoW,因为它可以通过在local spatial bins中池化来保持空间信息。这些spatial bins的大小与图像大小成正比,所以无论图像大小如何,bins的数量都是固定的。这与之前深度网络[3]的滑动窗口池化不同,滑动窗口的数量取决于输入大小。
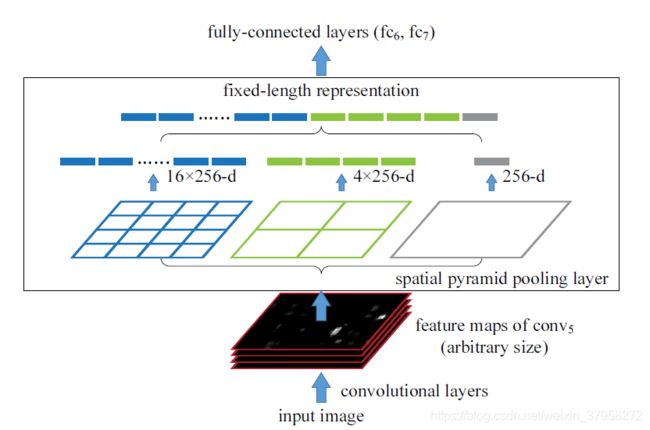
图3:空间金字塔汇集层的网络结构。这里256是 c o n v 5 conv_5 conv5层的滤波器号, c o n v 5 conv_5 conv5是最后一个卷积层。
为了对任意大小的图像采用深度网络,我们用一个空间金字塔池化层代替最后一个池化层(例如,池5,在最后一个卷积层之后)。图3说明了我们的方法。在每个空间仓中,我们对每个滤波器的响应进行池化(在本文中,我们使用最大池化)。空间金字塔池化的输出是kM维向量,宾格数表示为M(k是最后一个卷积层中滤波器的数量)。固定维向量是全连接层的输入。
**通过空间金字塔池,输入图像可以是任何尺寸。这不仅允许任意的长宽比,而且允许任意的大小。我们可以将输入图像调整到任何尺度(例如,min(w,h)=180,224,…),并应用同一个深度网络。当输入图像处于不同的尺度时,网络(在相同的滤波器尺寸下)将提取不同尺度的特征。**尺度在传统方法中扮演着重要的角色,例如,SIFT向量通常在多个尺度下提取[29],[27](由补丁和高斯滤波器的大小决定)。我们将表明,尺度对深度网络的精度也很重要。
有趣的是,coarsest pyramid level有一个覆盖整个图像的single bin。这其实是一种 "全局池化 "的操作,在一些同当前的工作中也有研究。在[31]、[32]中,采用全局平均池化来减小模型大小,同时也减轻了过拟合影响;在[33]中,测试阶段所有fc层之后采用全局平均池化来提高精度;在[34]中,全局最大池化用于弱监督对象识别。全局池化操作对应于传统的Bag-of-Words方法。
2.3 Training the Network
理论上,上述网络结构可以用标准的反向传播[1]进行训练,而不考虑输入图像的大小。但在实践中,GPU的实现(如cuda-convnet[3]和Caffe[35])最好是在固定的输入图像上运行。接下来我们将描述我们的训练方案,它利用这些GPU实现,同时仍然保留了空间金字塔池行为。
Single-size training
图4:cuda-convnet风格的3级金字塔池化示例[3]。这里sizeX是池化窗口的大小。此配置用于 c o n v 5 conv_5 conv5 feature map size为 13 × 13 13\times13 13×13的网络,所以 p o o l 3 × 3 pool_{3\times3} pool3×3, p o o l 2 × 2 pool_{2\times2} pool2×2, p o o l 1 × 1 pool_{1\times1} pool1×1层分别有 3 × 3 , 2 × 2 , 1 × 1 3\times3,2\times2,1\times1 3×3,2×2,1×1bins。
与之前的工作一样,我们首先考虑一个网络从图像中提取一个固定尺寸的输入(224x224)进行裁剪。裁剪的目的是为了数据增强。对于给定尺寸的图像,我们可以预先计算空间金字塔池化所需的bin大小。考虑conv5后的特征图,其大小为axa(如13x13)。在nxn个bins的pyramid level,我们将这个池化级别实现为滑动窗口池化,其中窗口大小为 w i n = ⌈ a / n ⌉ win=\lceil a/n\rceil win=⌈a/n⌉,步长 s t r = ⌊ a / n ⌋ str=\lfloor a/n\rfloor str=⌊a/n⌋。其中 ⌈ ⋅ ⌉ \lceil \cdot\rceil ⌈⋅⌉和 ⌊ ⋅ ⌋ \lfloor\cdot\rfloor ⌊⋅⌋代表上取整和下取整操作。通过一个l-level金字塔,我们实现了l个这样的层。下一个全连接层(fc6)将把这l个输出concatenate。图4显示了cuda-convnet风格的3级金字塔池(3x3,2x2,1x1)的配置实例[3]。
我们进行single-size训练的主要目的是为了实现multi-level pooling。实验表明,这是获得准确率的原因之一。
Multi-size training
我们的SPP网络有望应用在任何尺寸的图像上。为了解决训练中图像尺寸变化的问题,我们考虑一组预定义的尺寸。我们考虑两种尺寸。180x180以及224x224。我们不是裁剪一个较小的180x180区域,而是将上述224x224区域调整为180x180。因此,两种尺度的区域只在分辨率上有差异,而在content/layout上没有差异。为了让网络接受180x180的输入,我们实现了另一个固定大小的输入(180x180)网络, c o n v 5 conv_5 conv5的特征图大小为 a × a = 10 × 10 a\times a=10\times10 a×a=10×10,我们依然采用 w i n = ⌈ a / n ⌉ win = \lceil a/n \rceil win=⌈a/n⌉和 s t r = ⌊ a / n ⌋ str=\lfloor a/n\rfloor str=⌊a/n⌋实现各金字塔级池化。这个180-网络的spatialp yramid pooling的输出与224-网络的固定长度相同。因此,这个180网络与224网络的参数完全相同。224-网络中的每一层。换句话说,在训练过程中,我们通过两个共享参数的固定大小的网络来实现不同输入大小的SPP-net。
为了减少从一个网络(如224)切换到另一个网络(如180)的开销,我们在一个网络上训练每个完整的epoch,然后在下一个完整的epoch切换到另一个网络(保持所有权重)。这样反复进行。在实验中,我们发现这种多尺寸训练的收敛率与上述单尺寸训练相似。
我们的多尺寸训练的主要目的是模拟不同的输入尺寸,同时仍然利用现有的优化的固定尺寸实现。除了上述两个规模的实现,我们还测试了一个使用s x s作为输入的变体,其中s是在每个epoch从[180,224]中随机和均匀地采样。我们在实验部分报告了这两种变体的结果。
需要注意的是,以上单/多尺寸解决方案仅用于训练。在测试阶段,可以直接将SPP-net应用到任何尺寸的图像上。
3 SPP-NET FOR IMAGE CLASSIFICATION
3.1 Experiments on ImageNet 2012 Classification
我们在ImageNet 2012的1000类训练集上训练网络。我们的训练算法沿用了之前工作[3]、[4]、[36]的做法。图像被调整大小,使较小的维度为256,并从整个图像的中心或四个角选取224x224的裁剪1。通过水平翻转和颜色改变[3]对数据进行增强。在两个完全连接的层上使用Dropout[3]。学习率从0.01开始,当误差达到平缓时除以10(两次)。我们的实现是基于cuda-convnet[3]和Caffe[35]的公开代码。本文中的所有网络都可以在两到四周内,在单个GeForce GTX Titan GPU(6 GB内存)上进行训练。
3.1.1 Baseline Network Architectures
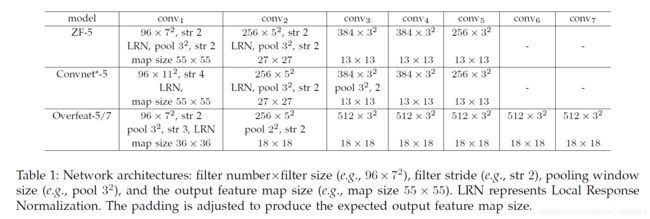
SPP的优势与使用的卷积网络架构无关。我们研究了现有出版物[3]、[4]、[5]中的四种不同的网络架构(或它们的修改),我们表明SPP提高了所有这些架构的精度。这些基线架构见表1,下面简单介绍一下。
ZF-5:这个架构是基于Zeiler和Fergus(ZF)的 “快速”(较小)模型[4]。数字表示五个卷积层。
Convnet*-5:这是对Krizhevsky等人的网络[3]的修改。我们把两个池化层放在conv2和conv3之后(而不是conv1和conv2之后)。因此,每层之后的特征图的大小与ZF-5相同。
Overfeat-5/7:该架构基于Overfeat论文[5],并做了一些修改,如[6]。与ZF-5/Convnet*-5相比,这个架构在最后一个池化层之前会产生一个更大的特征图(1818而不是13 13)。一个较大的滤波器数量(512)被用于conv3和以下卷积层。我们还研究了7个卷积层的更深层次的架构,其中conv3到conv7具有相同的结构。
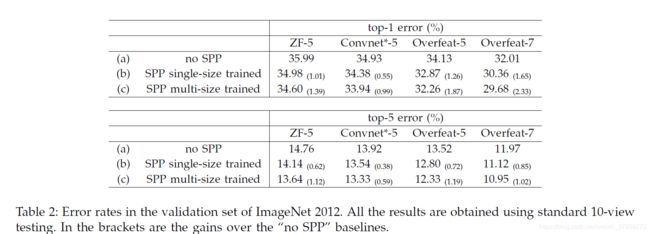
在基线模型中,最后一个卷积层之后的池化层会生成66个特征图,之后是两个4096-d的fc层和一个1000路的softmax层。我们对这些基线网络的复制情况见表2(a)。我们为ZF-5训练了70个epoch,为其他网络训练了90个epoch。我们对ZF-5的复制比[4]中报道的要好。这种增益是因为角部裁剪是来自整个图像,这在[36]中也有报道。
3.1.2 Multi-level Pooling Improves Accuracy
在表2(b)中,我们显示了使用singlesize训练的结果。训练和测试大小都是224x224。在这些网络中,卷积层的结构与相应的基线模型相同,而最后卷积层之后的池化层则被SPP层取代。对于表2中的结果,我们使用4层金字塔。金字塔为{6x6,3x3,2x2,1x1}。(共50个bin)。为了公平比较,我们仍然使用标准的10视图预测,每个视图都是224x224的裁剪。我们在表2(b)中的结果显示出比表2(a)中的无SPP基线有相当大的改进。有趣的是,top-1误差的最大收益(1.65%)是由最精确的架构给出的。由于我们仍然使用与(a)相同的10个裁剪视图,这些增益完全是因为multi-level pooling。
值得注意的是,multi-level pooling的收益并不只是因为参数多,而是因为多级池化对物体变形和空间布局的变异具有鲁棒性[15]。为了证明这一点,我们用不同的4层金字塔训练另一个ZF-5网络。{4x4, 3x3, 2x2, 1x1}(共30个bins)。
这个网络的参数比没有SPP的网络少,因为它的fc6层有30x256-d的输入,而不是36x256-d。该网络的top-1/top-5误差为35.06/14.04。这个结果与上面的50-bin金字塔相似(34.98/14.14),但比无SPP的对应网络(35.99/14.76)要好得多。
3.1.3 Multi-size Training Improves Accuracy
表2(c)显示了我们使用多尺寸训练的结果。训练大小为224和180,而测试大小仍为224。我们仍然使用标准的10-view prediction。所有架构的top-1/top-5误差进一步下降。SPP-net(Overfeat-7)的top-1误差下降到29.68%,比无SPP的同类产品好2.33%,比单尺寸训练的同类产品好0.68%。
除了使用180和224这两个离散尺寸外,我们还使用从[180,224]中均匀抽取的随机尺寸进行评估。SPP-net(Overfeat-7)的top-1/5误差为30.06%/10.96%。top-1误差比two-size版本稍差,可能是因为224的大小(用于测试)访问量较少。但结果还是比单尺寸版本好。
之前有一些CNN的解决方案[5]、[36],处理各种规模/大小的问题,但它们大多是基于测试的。在Overfeat[5]和Howard的方法[36]中,单一网络在测试阶段应用于多个尺度,并对分数进行平均。Howard进一步在低/高分辨率图像区域上训练两个不同的网络,并对分数进行平均。据我们所知,我们的方法是第一个用多种规模的输入图像训练单一网络的方法。
3.1.4 Full-image Representations Improve Accuracy
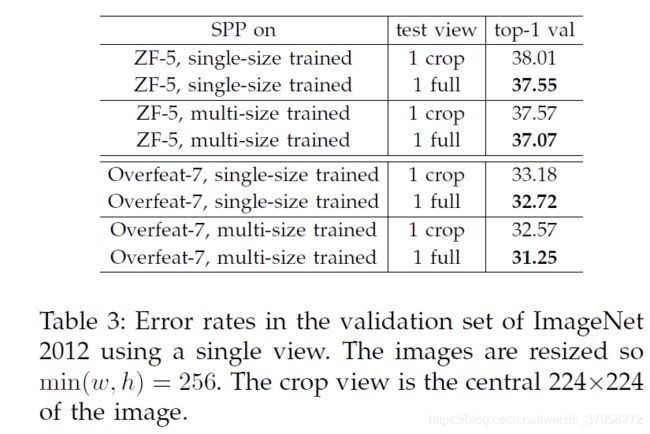
接下来我们研究full-image view的精度。我们调整图像的大小,使min(w,h)=256,同时保持其长宽比。SPP-net应用于该full image计算full view的得分。为了公平比较,我们还评估了中心224x224裁剪的single view的准确性(上述评估中使用的是它)。single view测试精度的比较见表3。这里我们评估的是ZF-5/Overfeat-7。通过full-view representation,top-1的错误率都有所降低。这说明保持完整内容的重要性。即使我们的网络只使用正方形图像进行训练,它也能很好地泛化到其他纵横比。
对比表2和表3,我们发现multiple views的组合大大优于single full-image view。然而,fullimage representations仍然具有良好的优点。首先,我们实证发现(在下一小节讨论),即使是combination of dozens of views,额外的两个full-image views(带翻转)仍然可以提升约0.2%的精度。第二,full-image与传统的方法[15]、[17]、[19]在方法上是一致的,传统的方法是将整个图像的编码SIFT向量集中在一起。第三,在其他应用中,如图像检索[37],相似度排名需要的是图像表示,而不是分类得分。可以首选全图像表示法。
views(带翻转)仍然可以提升约0.2%的精度。第二,full-image与传统的方法[15]、[17]、[19]在方法上是一致的,传统的方法是将整个图像的编码SIFT向量集中在一起。第三,在其他应用中,如图像检索[37],相似度排名需要的是图像表示,而不是分类得分。可以首选全图像表示法。