机器学习（10）-随机森林案例（调参）之公共自行车使用量预测

1. 前言

1.1 背景介绍

公共自行车低碳，环保，健康，并且解决了交通中“最后一公里”的痛点，在全国各个城市越来越受欢迎。本次数据取自于两个城市某街道上的几处公共自行车停车桩。希望根据时间，天气等信息，预测出该街区在一小时内的被借取的公共自行车的数量。

1.2 任务类型

回归

1.3 数据文件说明

数据集	作用	说明
train.csv	训练集	文件大小为273KB
test.csv	测试集	文件大小为179KB

1.4 数据变量说明

训练集中共有10000条样本，预测集中有7000条样本

变量名	解释
id	行编号
y	一小时内自行车被借取的数量，在测试集中是需要被预测的数值
city	表示该行记录所发生的城市
hour	当时的时间，精确到小时，24小时计时法
is_workday	1表示工作日，0表示节假日或周末
temp_1	当时的气温，单位为摄氏度
temp_2	当时的体感温度，单位为摄氏度
weather	当时的天气状况，1为晴朗，2为多云、阴天，3为小雨，4为大雨
wind	当时的风速，数值越大风速越大

1.5 评估方法

评价方法为RMSE（Root of Mean Squared Error）

若真实值为$y=(y_1,y_2,...,y_n)$，模型的预测值为$\hat{y}=({\hat{y}}_1,{\hat{y}}_2,...,{\hat{y}}_n)$，那么该模型的RMSE的计算公式为：
$$RMSE=\sqrt{\frac{{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2}{n}}$$
RMSE越小，说明模型预测得越准。

2. 数据预处理

2.1 观察数据有没有缺失值

print(traindata.info())

输出：

RangeIndex: 10000 entries, 0 to 9999
Data columns (total 7 columns):
city          10000 non-null int64
hour          10000 non-null int64
is_workday    10000 non-null int64
weather       10000 non-null int64
temp_1        10000 non-null float64
temp_2        10000 non-null float64
wind          10000 non-null int64
dtypes: float64(2), int64(5)
memory usage: 547.0 KB
None

我们可以看到，共有10000个观测值，没有缺失值。

2.2 观察每个变量的基础描述信息

print(traindata.describe())

输出：

                 city          hour    is_workday      weather  \
count    10000.000000  10000.000000  10000.000000  10000.00000   
mean         0.499800     11.527500      0.684000      1.42750   
std          0.500025      6.909777      0.464936      0.63764   
min          0.000000      0.000000      0.000000      1.00000   
25%          0.000000      6.000000      0.000000      1.00000   
50%          0.000000     12.000000      1.000000      1.00000   
75%          1.000000     18.000000      1.000000      2.00000   
max          1.000000     23.000000      1.000000      4.00000 
             temp_1        temp_2          wind             y  
count  10000.000000  10000.000000  10000.000000  10000.000000  
mean      15.268190     15.321230      1.248600     50.537400  
std        9.029152     11.308986      1.095773     47.769645  
min       -7.600000    -15.600000      0.000000      0.000000  
25%        7.800000      5.800000      0.000000     10.000000  
50%       15.600000     16.000000      1.000000     39.000000  
75%       22.600000     24.800000      2.000000     75.000000  
max       38.600000     46.800000      7.000000    249.000000 

通过观察可以得出一些猜测，如根据温度得信息可以排除南方城市；整个观测记录时间跨度较长，还可能包含了一个长假期数据等等。

2.3 查看相关系数

为了方便查看，绝对值低于0.2的就用nan替代

corr = traindata.corr()
corr[np.abs(corr) < 0.2] = np.nan
print(corr)

输出：

               city      hour  is_workday  weather    temp_1    temp_2  \
city           1.0       NaN         NaN      NaN       NaN       NaN   
hour           NaN  1.000000         NaN      NaN       NaN       NaN   
is_workday     NaN       NaN         1.0      NaN       NaN       NaN   
weather        NaN       NaN         NaN      1.0       NaN       NaN   
temp_1         NaN       NaN         NaN      NaN  1.000000  0.987357   
temp_2         NaN       NaN         NaN      NaN  0.987357  1.000000   
wind           NaN       NaN         NaN      NaN       NaN       NaN   
y              NaN  0.406489         NaN      NaN  0.417115  0.413942   

            wind         y  
city         NaN       NaN  
hour         NaN  0.406489  
is_workday   NaN       NaN  
weather      NaN       NaN  
temp_1       NaN  0.417115  
temp_2       NaN  0.413942  
wind         1.0       NaN  
y            NaN  1.000000  

从相关性角度来看，用车的时间和当时的气温对借取数量y有较强的关系；气温和体感气温显强正相关（共线性），这个和常识一致。

3. 模型训练及其结果展示

3.1 标杆模型：简单线性回归模型

该模型预测结果的RMSE为：39.132

# -*- coding: utf-8 -*-
 
# 引入模块
from sklearn.linear_model import LinearRegression
import pandas as pd
 
# 读取数据
train = pd.read_csv("train.csv")
test = pd.read_csv("test.csv")
submit = pd.read_csv("sample_submit.csv")
 
# 删除id
train.drop('id', axis=1, inplace=True)
test.drop('id', axis=1, inplace=True)
 
# 取出训练集的y
y_train = train.pop('y')
 
# 建立线性回归模型
reg = LinearRegression()
reg.fit(train, y_train)
y_pred = reg.predict(test)
 
# 若预测值是负数，则取0
y_pred = map(lambda x: x if x >= 0 else 0, y_pred)
 
# 输出预测结果至my_LR_prediction.csv
submit['y'] = y_pred
submit.to_csv('my_LR_prediction.csv', index=False)

3.2 决策树回归模型

该模型预测结果的RMSE为：28.818

# -*- coding: utf-8 -*-
 
# 引入模块
from sklearn.tree import DecisionTreeRegressor
import pandas as pd
 
# 读取数据
train = pd.read_csv("train.csv")
test = pd.read_csv("test.csv")
submit = pd.read_csv("sample_submit.csv")
 
# 删除id
train.drop('id', axis=1, inplace=True)
test.drop('id', axis=1, inplace=True)
 
# 取出训练集的y
y_train = train.pop('y')
 
# 建立最大深度为5的决策树回归模型
reg = DecisionTreeRegressor(max_depth=5)
reg.fit(train, y_train)
y_pred = reg.predict(test)
 
# 输出预测结果至my_DT_prediction.csv
submit['y'] = y_pred
submit.to_csv('my_DT_prediction.csv', index=False)

3.3 随机森林回归模型

该模型预测结果的RMSE为：18.028

#_*_coding:utf-8_*_
import numpy as np
import pandas as pd
 
 
def load_data(trainfile, testfile):
    traindata = pd.read_csv(trainfile)
    testdata = pd.read_csv(testfile)
    feature_data = traindata.iloc[:, 1:-1]
    label_data = traindata.iloc[:, -1]
    test_feature = testdata.iloc[:, 1:]
    return feature_data, label_data, test_feature
 
def random_forest_train(feature_data, label_data):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
 
    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
 
    model = RandomForestRegressor()
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)
 
if __name__ == '__main__':
    trainfile = 'data/train.csv'
    testfile = 'data/test.csv'
    submitfile = 'data/sample_submit.csv'
    feature_data, label_data = load_data(trainfile, testfile)
    random_forest_train(feature_data, label_data)

3.4 随机森林回归模型调参过程说明

3.4.1 RF Bagging框架参数

参考博客
RF框架参数比较简单，因为Bagging框架里的各个弱学习器之间是没有依赖关系的，这减小调参的难度。

下面来看看RF重要的Bagging框架的参数，由于RandomForestClassifier和RandomForestRegressor参数绝大部分相同，这里会将它们一起讲，不同点会指出。

1. n_estimators ：也就是弱学习器的最大迭代次数，或者说最大的弱学习器的个数。一般来说n_estimators太小，容易欠拟合，n_estimators太大，又容易过拟合，一般选择一个适中的数值。RandomForestClassifier和RandomForestRegressor默认是10。在实际调参的过程中，常常将n_estimators和下面介绍的参数learning_rate一起考虑。
2. oob_score：即是否采用袋外样本来评估模型的好坏。默认识False。有放回采样中大约36.8%的没有被采样到的数据，常常称之为袋外数据（Out Of Bag 简称OOB），这些数据没有参与训练集模型的拟合，因此可以用来检测模型的泛化能力。推荐设置为True，因为袋外分数反应了一个模型拟合后的泛化能力。
3. criterion： 即CART树做划分时对特征的评价标准。分类模型和回归模型的损失函数是不一样的。分类RF对应的CART分类树默认是基尼系数gini,另一个可选择的标准是信息增益。回归RF对应的CART回归树默认是均方差mse，另一个可以选择的标准是绝对值差mae。一般来说选择默认的标准就已经很好。
4. bootstrap：默认是True，是否有放回的采样。
5. verbose：日志亢长度，int表示亢长度，o表示输出训练过程，1表示偶尔输出 ，>1表示对每个子模型都输出

从上面可以看出， RF重要的框架参数比较少，主要需要关注的是 n_estimators，即RF最大的决策树个数。当使用这些方法的时候，最主要的参数是调整n_estimators和max_features。n_estimators指的是森林中树的个数，树数目越大越好，但是会增加计算开销，另外，注意如果超过限定数量后，计算将会停止。

3.4.2 RF决策树参数

1. RF划分时考虑的最大特征数max_features: 可以使用很多种类型的值，默认是"None",意味着划分时考虑所有的特征数；如果是"log2"意味着划分时最多考虑log2(n_features)个特征；如果是"sqrt"或者"auto"意味着划分时最多考虑sqrt(n_features)个特征。如果是整数，代表考虑的特征绝对数。如果是浮点数，代表考虑特征百分比，即考虑（百分比xN）取整后的特征数。其中N为样本总特征数。一般来说，如果样本特征数不多，比如小于50，我们用默认的"None"就可以了，如果特征数非常多，我们可以灵活使用刚才描述的其他取值来控制划分时考虑的最大特征数，以控制决策树的生成时间。max_features指的是，当划分一个节点的时候，features的随机子集的size，该值越小，variance会变小，但是bais会变大。（int 表示个数，float表示占所有特征的百分比，auto表示所有特征数的开方，sqrt表示所有特征数的开放，log2表示所有特征数的log2值，None表示等于所有特征数）
2. 决策树最大深度max_depth: 默认可以不输入，如果不输入的话，决策树在建立子树的时候不会限制子树的深度。一般来说，数据少或者特征少的时候可以不管这个值。如果模型样本量多，特征也多的情况下，推荐限制这个最大深度，具体的取值取决于数据的分布。常用的可以取值10-100之间。（int表示深度，None表示树会生长到所有叶子都分到一个类，或者某节点所代表的样本已小于min_samples_split）
3. 内部节点再划分所需最小样本数min_samples_split: 这个值限制了子树继续划分的条件，如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分。 默认是2.如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。（int表示样本数，2表示默认值）
4. 叶子节点最少样本数min_samples_leaf: 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝。 默认是1,可以输入最少的样本数的整数，或者最少样本数占样本总数的百分比。如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。
5. 叶子节点最小的样本权重和min_weight_fraction_leaf：这个值限制了叶子节点所有样本权重和的最小值，如果小于这个值，则会和兄弟节点一起被剪枝。 默认是0，就是不考虑权重问题。一般来说，如果我们有较多样本有缺失值，或者分类树样本的分布类别偏差很大，就会引入样本权重，这时我们就要注意这个值了。
6. 最大叶子节点数max_leaf_nodes: 通过限制最大叶子节点数，可以防止过拟合，默认是"None”，即不限制最大的叶子节点数。如果加了限制，算法会建立在最大叶子节点数内最优的决策树。如果特征不多，可以不考虑这个值，但是如果特征分成多的话，可以加以限制，具体的值可以通过交叉验证得到。
7. 节点划分最小不纯度min_impurity_split: 这个值限制了决策树的增长，如果某节点的不纯度(基于基尼系数，均方差)小于这个阈值，则该节点不再生成子节点。即为叶子节点 。一般不推荐改动默认值1e-7。
8. 用于拟合和预测的并行运行的工作数量n_jobs：一般取整数，可选的（默认值为1），如果为-1，那么工作数量被设置为核的数量，机器上所有的核都会被使用（跟CPU核数一致）。如果n_jobs=k，则计算被划分为k个job，并运行在K核上。注意，由于进程间通信的开销，加速效果并不会是线性的（job数K不会提示K倍）通过构建大量的树，比起单颗树所需要的时间，性能也能得到很大的提升，
9. 随机数生成器random_state：随机数生成器使用的种子，如果是RandomState实例，则random_stats就是随机数生成器；如果为None，则随机数生成器是np.random使用的RandomState实例。

根据经验：

对于回归问题：好的缺省值max_features = n_features;

对于分类问题：好的缺省值是max_features=sqrt(n_features)。n_features指的是数据中的feature总数。

当设置max_depth=None，以及min_samples_split=1时，通常会得到好的结果（完全展开的树）。但需要注意，这些值通常不是最优的，并且会浪费RAM内存。最好的参数应通过cross-validation给出。另外需要注意：

1. 在随机森林中，缺省时会使用bootstrap进行样本抽样(bootstrap=True) ；
2. 当使用bootstrap样本时，泛化误差可能在估计时落在out-of-bag样本中。此时，可以通过设置oob_score=True来开启。

3.4.3 RF调参

参数分类的目的在于缩小调参的范围，首先要明确训练的目标，把目标类的参数定下来。接下来，需要根据数据集的大小，考虑是否采用一些提高训练效率的策略，否则一次训练就三天三夜，时间太久了，所以需要调整那些影响整体的模型性能的参数。

1. 调参的目标：偏差和方差的协调

偏差和方差通过准确率来影响着模型的性能。调参的目标就是为了达到整体模型的偏差和方差的大和谐。进一步，这些参数又可以分为两类：过程影响类及子模型影响类。在子模型不变的前提下，某些参数可以通过改变训练的过程，从而影响着模型的性能，诸如：“子模型数”（n_estimators），“学习率”（learning_rate）等，另外，还可以通过改变子模型性能来影响整体模型的性能，诸如：“最大树深度”（max_depth），‘分裂条件’（criterion）等。正由于Bagging的训练过程旨在降低方差，而Boosting的训练过程旨在降低偏差，过程影响类的参数能够引起整体模型性能的大幅度变化。一般来说，在此前提下，继续微调子模型影响类的参数，从而进一步提高模型的性能。

2. 参数对整体模型性能的影响

假设模型是一个多元函数F，其输出值为模型的准确度。可以固定其他参数，从而对某个参数整体模型性能的影响进行分析：是正影响还是负影响，影响的单调性是如何的。

对Random Forest来说，增加“子模型树”（n_estimators）可以明显降低整体模型的方差，且不会对子模型的偏差和方差有任何影响。模型的准确度会随着“子模型数”的增加而提高，由于减少的是整体模型方差公式的第二项，故准确度的提高有一个上线。在不同的场景下，“分裂条件”（criterion）对模型的准确度的影响也不一样，该参数需要在实际运行时灵活调整。调整“最大叶子节点数”（max_leaf_models）以及“最大树深度”（max_depth）之一，可以粗粒度地调整树的结构：叶节点越多或者树越深，意味着子模型的偏差月底，方差越高；同时，调整”分裂所需要最小样本数”（min_samples_split），“叶节点最小样本数”（min_samples_leaf）及“叶节点最小权重总值”（min_weight_fraction_leaf），可以更细粒度地调整树的结构：分裂所需样本数越少或者叶节点所需样本越少，也意味着子模型越复杂。一般来说，我们总采用bootstrap对样本进行子采样来降低子模型之间的关联度，从而降低整体模型的方差。适当地减少“分裂时考虑的最大特征数”（max_features），给子模型注入了另外的随机性，同样也达到了降低子模型之间关联度的效果。但是一味地降低该参数也是不行的，因为分裂时可选特征变少，模型的偏差会越来越大。在下图中，可以看到这些参数对Random Forest整体模型性能的影响：

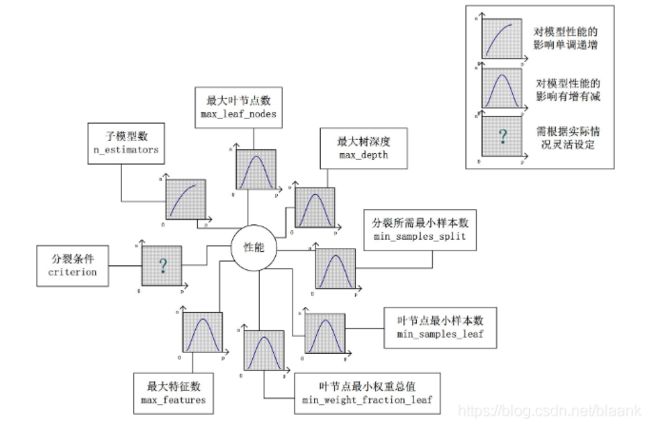
3. 调参步骤

1. 首先先调既不会增加模型复杂度，又对模型影响最大的参数n_estimators（学习曲线）
2. 找到最佳值后，调max_depth（单个网格搜索，也可以使用学习曲线）
   一般根据数据的大小来进行一个探视，当数据集很小的时候，可以采用1_10，或者120这样的试探，但是对于大型数据来说，应该尝试30~50 层深度（或许更深）
3. 接下来依次对各个参数进行调参
   　注意：
   　- 对大型数据集，max_leaf_nodes可以尝试从1000来构建，先输入1000，每100个叶子一个区间，再逐渐缩小范围
   　- 对于min_samples_split 和 min_samples_leaf，一般从他们的最小值开始向上增加10或者20，面对高纬度高样本数据，如果不放心可以直接50+，对于大型数据可能需要200~300的范围，如果调整的时候发现准确率无论如何都上不来，可以放心大胆的调试一个很大的数据，大力限制模型的复杂度

3.5 随机森林回归模型调参

3.5.1 使用gridsearchcv探索n_estimators的最佳值

def random_forest_parameter_tuning1(feature_data, label_data):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV
 
    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    param_test1 = {
     
        'n_estimators': range(10, 100, 10)
    }
    model = GridSearchCV(estimator=RandomForestRegressor(
        min_samples_split=100, min_samples_leaf=20, max_depth=8, max_features='sqrt',
        random_state=10), param_grid=param_test1, cv=5
    )
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)
    return model.best_score_, model.best_params_

输出：

best n_estimators_RMSE: 19.64849505163415
params: {
     'n_estimators': 70}

这样得到了最佳的弱学习器迭代次数，为70.。

3.5.2 对决策树最大深度 max_depth 求最佳值

得到了最佳弱学习器迭代次数，接着对决策树最大深度max_depth和内部节点再划分所需要最小样本数min_samples_split进行网格搜索。

def random_forest_parameter_tuning2(feature_data, label_data):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV
 
    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    param_test2 = {
     
        'max_depth': range(3, 20, 1)
    }
    model = GridSearchCV(estimator=RandomForestRegressor(
        n_estimators=70, min_samples_leaf=20, max_features='sqrt', oob_score=True,
        random_state=10), param_grid=param_test2, cv=5
    )
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print("best max_depth：", RMSE)
    print("params:", model.best_params_)
    return model.best_score_, model.best_params_

输出：

best max_depth： 17.076022082821094
params: {
     'max_depth': 14}

这样得到了最佳的决策树最大深度，为14。

3.5.3 求内部节点再划分所需要的最小样本数min_samples_split和叶子节点最小样本数min_samples_leaf的最佳参数

下面对内部节点在划分所需要最小样本数min_samples_split和叶子节点最小样本数min_samples_leaf一起调参。

def random_forest_parameter_tuning3(feature_data, label_data):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV
 
    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    param_test3 = {
     
        'min_samples_split': range(2, 10, 2),
        'min_samples_leaf': range(2, 10, 2),
    }
    model = GridSearchCV(estimator=RandomForestRegressor(
        n_estimators=70, max_depth=14, max_features='sqrt', oob_score=True,
        random_state=10), param_grid=param_test3, cv=5
    )
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print("best min_sample_leaf and min_sample_split:", RMSE)
    print("params:", model.best_params_)
    return model.best_score_, model.best_params_

输出：

best min_sample_leaf and min_sample_split: 14.524410925030937
params: {
     'min_samples_leaf': 2, 'min_samples_split': 8}

3.5.4 求最大特征数max_features的最佳参数

def random_forest_parameter_tuning4(feature_data, label_data):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
    from sklearn.model_selection import GridSearchCV
 
    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    param_test3 = {
     
        'max_features': range(3, 9, 2),
    }
    model = GridSearchCV(estimator=RandomForestRegressor(
        n_estimators=70, max_depth=13, min_samples_split=10, min_samples_leaf=10, oob_score=True,
        random_state=10), param_grid=param_test3, cv=5
    )
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print("best max_features:", RMSE)
    print("params:", model.best_params_)
    return model.best_score_, model.best_params_

输出：

best max_features: 15.178957907919308
params: {
     'max_features': 7}

3.5.5 汇总搜索到的最佳参数，然后训练

def random_forest_train(feature_data, label_data, test_feature, submitfile):
    from sklearn.ensemble import RandomForestRegressor
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_squared_error
 
    X_train, X_test, y_train, y_test = train_test_split(feature_data, label_data, test_size=0.23)
    params = {
     
        'n_estimators': 70,
        'max_depth': 14,
        'min_samples_split': 8,
        'min_samples_leaf': 2,
        'max_features': 7
    }
    model = RandomForestRegressor(**params)
    model.fit(X_train, y_train)
    # 对测试集进行预测
    y_pred = model.predict(X_test)
    # 计算准确率
    MSE = mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    print(RMSE)

输出：

random_forest_train_RMSE: 14.492368274315185

经过调参，结果由18.028优化到了14.492

参考资料

https://www.cnblogs.com/wj-1314/p/9628303.html
气温预测
100天搞定机器学习