计算机视觉算法——图像分类网络总结
计算机视觉算法——图像分类网络总结
- 计算机视觉算法——图像分类网络总结
-
- 1. AlexNet
-
- 1.1 网络结构
- 1.2 关键知识点
-
- 1.2.1 卷积和池化特征尺寸计算公式
- 1.2.2 ReLU非线性激活函数
- 1.2.3 防止过拟合
- 2. VGG
-
- 2.1 网络结果
- 2.2 关键知识点
-
- 2.2.1 感受野的计算以及大小卷积核
- 3. GoogLeNet
-
- 3.1 网络结构
- 3.2 关键知识点
-
- 3.2.1 Inception结构
- 3.2.2 1 × 1 1 \times 1 1×1卷积作用
- 3.2.3 辅助分类器
- 4. ResNet
-
- 4.1 网络结构
- 4.2 关键知识点
-
- 4.2.1 residual模块
- 4.2.2 batch normalization
- 5. ResNeXt
-
- 5.1 网络结构
- 5.2 关键知识点
-
- 5.2.1 分组卷积
- 6. MobileNet
-
- 6.1 网络结构
- 6.2 关键知识点
-
- 6.2.1 Depthwise Separable Convolution
- 6.2.2 Inverted Residuals Block 和 Linear Bottleneck
- 7. ShuffleNet
-
- 7.1 网络结构
- 7.2 关键知识点
-
- 7.2.1 Channel Shuffle思想
- 8. EfficientNet
- 总结
计算机视觉算法——图像分类网络总结
由于后面工作方向的需要，也是自己的兴趣，我决定补习下计算机视觉算法相关的知识点，参考的学习资料主要是B站Up主霹雳吧啦Wz，强推一下，Up主的分享非常的细致认真，从他这里入门是个不错的选择，Up主也有自己的CSDN博客，我这里主要是作为课程的笔记，也会加入一些自己的理解，我也只是个入门的小白，如果有错误还请读者指正。
要入门基于DNN的计算机视觉，分类网络构架是基础，分类网络会作为各种衍生网络的backbone，也就是重要组成部分，起到了提取特征等作用，下面开始逐个总结各个图像分类网络的特点。
1. AlexNet
AlexNet是2012年CVPR发表的一篇革命性的论文，现在的引用量都快接近8w了，它的主要创新点是：
- 首次利用GPU进行网络加速训练；
- 使用了RxeLU激活函数，而不是传统的SIgmoid激活函数以及Tanh激活函数；
- 使用了LRN局部响应归一化；
- 在全连接层的前两层使用了Dropout随机失活神经元操作，以减少过拟合；
1.1 网络结构
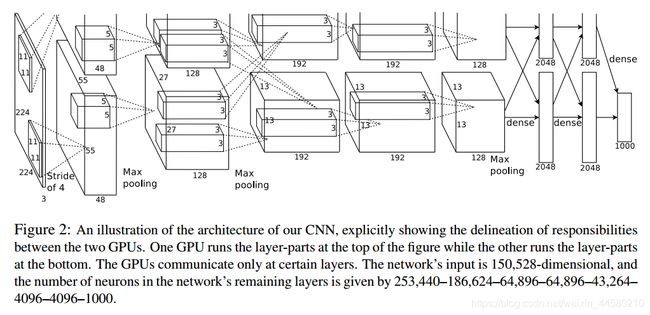
AlexNet网络由五层卷积加三层最大池化层，以及最后三层的全连接层构成，那会儿由于GPU显存不够大，因此作者采用的方式是将一张图一份为二，分别使用两张GPU训练，在进行第三层卷积时会将两张GPU的输出进行联合输入，在其他层数据都是独立的。
1.2 关键知识点
1.2.1 卷积和池化特征尺寸计算公式
AlexNet中主要是使用了卷积和最大池化层，卷积后特征尺寸计算公式为： N = ( W − F + 2 P ) / S + 1 N=(W-F+2 P) / S+1 N=(W−F+2P)/S+1其中，输入特征尺寸为 W W W，卷积核的大小为 F × F F \times F F×F，卷积步daxiao长为 S S S，padding的像素数为 P P P，那么输出特征尺寸即为 N N N。池化可以看作一种特殊的卷积核，因此池化后特征尺寸计算同样满足上述规律。
1.2.2 ReLU非线性激活函数
ReLU非线性激活函数有如下优势：
- 可以使网络训练更快。 相比于sigmoid、tanh，导数更加好求，反向传播就是不断的更新参数的过程，因为其导数不复杂形式简单；
- 增加网络的非线性。 本身为非线性函数，加入到神经网络中可以是网格拟合非线性映射；
- 防止梯度消；
- 使网格具有稀疏性；
1.2.3 防止过拟合
AlexNet中使用两种方法减少过拟合，分别是：
- 数据扩增：对图片进行随机crop以及对RGB颜色空间进行调整
- Dropout：在训练阶段的每次前向传播中，都会重新进行 dropout。因此，每次有新的输入时，模型会被随机采样成不同的架构，但是所有的架构共享权值。该技术可以减少神经元之间的相互依赖性。因此，模型被强制学习更加稳健的特征。
2. VGG
VGG是2014年由牛津大学提出的，是应用非常广泛的一种backbone，此方法在提出时主要的贡献是：
- 文章提出通过堆叠多个 3 × 3 3 \times 3 3×3的卷积核可以代替大尺度卷积核，在保证相同感受野的前提下，增加了网络深度，并且 3 × 3 3\times3 3×3的卷积核更有利于保留图像性质，改善了网络效果。
2.1 网络结果
VGG网络的具体参数如下：
其中网络D包含16个隐藏层，称为VGG16，网络D包含19个隐藏层，称为VGG19，VGG16的结构如下图所示：
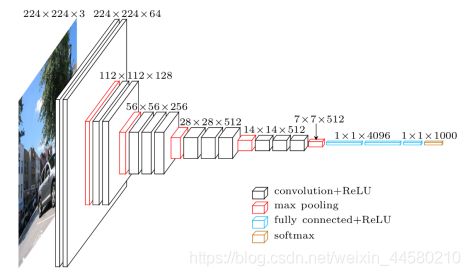
这里值得注意的一点是，在网络D中，卷积层中卷核大小为 3 × 3 3 \times 3 3×3，步距为1，padding为1，最大池化层的尺寸为2， 步距为2，因此我们可以计算经过卷积层后的特征尺寸不变，经过最大池化层后特征尺寸减半。此外最后三层为全连接层，占据了网络的绝大多数参数数量。
2.2 关键知识点
2.2.1 感受野的计算以及大小卷积核
这是VGG网路中最大的亮点，首先我们来了解下什么是感受野：在卷积神经网络中，决定某一层输出结果中一个元素对应的输入层的区域大小，称作感受野，也可以说是feature map上的一个单元对应输入层的区域的大小，如下图的例子：
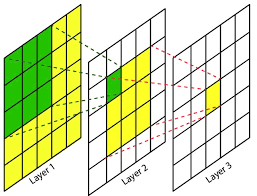
在上图中我们设置卷积核大小为 3 × 3 3\times3 3×3，步距为1，padding为0，按照前文的特征尺寸计算公式， 5 × 5 5\times5 5×5的特征，经过一层卷积后大小为 3 × 3 3\times3 3×3，再经过一层卷积后大小为 1 × 1 1\times1 1×1，感受野就是反过来推导， 1 × 1 1\times1 1×1的特征单元在两层卷积前对应的区域的大小即 5 × 5 5\times5 5×5，因此两层 3 × 3 3\times3 3×3的卷积核的感受野的大小即 5 × 5 5\times5 5×5，即可以代替一个 5 × 5 5\times5 5×5的卷积核。我们来计算下两种方法需要的参数数量，对于 5 × 5 5\times5 5×5的卷积核，参数数量为： 5 × 5 × C × C = 25 C 2 5 \times 5 \times C \times C = 25C^2 5×5×C×C=25C2对于两层 3 × 3 3\times3 3×3的卷积核，参数数量为： 3 × 3 × C × C + 3 × 3 × C × C = 18 C 2 3 \times 3 \times C \times C + 3 \times 3 \times C \times C = 18C^2 3×3×C×C+3×3×C×C=18C2由此可见，在感受野相同的情况下，叠加小卷积核的数量更小，并且网络更深，效果更有，并且有文章称 3 × 3 3\times3 3×3更有利于保持图像性质。
3. GoogLeNet
GoogLeNet的网络的亮点主要有：
- 引入Inception结构，用于融合不同尺寸的特征信息；
- 使用 1 × 1 1 \times 1 1×1的卷积核进行降维以及映射处理；
- 添加两个辅助分类器帮助训练
- 丢弃全连接层，使用平均池化层，大大减少模型参数；
3.1 网络结构
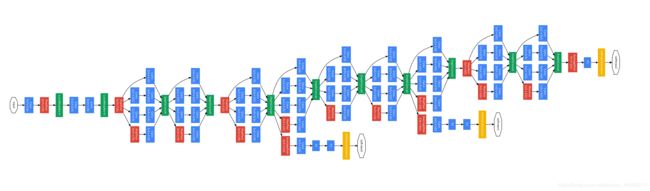
我们可以注意到，在AlexNet和VGG中都是串行处理，而在GoogLeNet通过Inception结构实现了并行处理，下面我们对Inception结构的细节进行讨论，
3.2 关键知识点
3.2.1 Inception结构
Inception结构设计的核心思想是，通过多个卷积核提取图像不同尺度的信息，最后进行融合，以得到图像更好的表征，我们以第三层的Inception结构为例，结构图如下：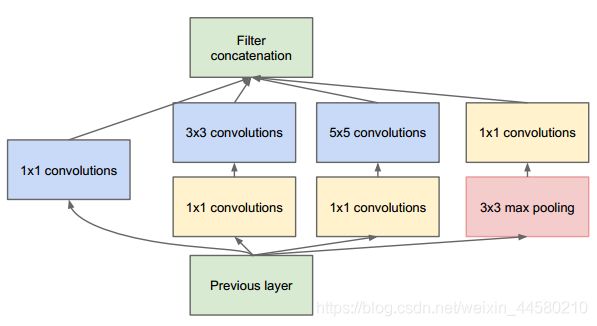
具体来说，分别是：
- 64个1x1的卷积核，然后RuLU，输出28x28x64；
- 96个1x1的卷积核，作为3x3卷积核之前的降维，变成28x28x96，然后进行ReLU计算，再进行128个3x3的卷积（padding为1），输出28x28x128；
- 16个1x1的卷积核，作为5x5卷积核之前的降维，变成28x28x16，进行ReLU计算后，再进行32个5x5的卷积（padding为2），输出28x28x32；
- pool层，使用3x3的核（padding为1），输出28x28x192，然后进行32个1x1的卷积，输出28x28x32。
最后将四个结果进行连接，对这四部分输出结果的第三维并联，即64+128+32+32=256，最终输出28x28x256，这一步操作称为concate。
3.2.2 1 × 1 1 \times 1 1×1卷积作用
1 × 1 1 \times 1 1×1卷积层引起人们重视是在NIN的网络结构中，在GoogLeNet网络中， 1 × 1 1 \times 1 1×1卷积层主要是用于降维和升维，目的在与减少网络计算量，同样以上述第三层的Inception结构为例，我们计算参数量： 1 × 1 × 192 × 64 + ( 1 × 1 × 192 × 96 + 3 × 3 × 96 × 128 ) + ( 1 × 1 × 192 × 16 + 5 × 5 × 16 × 32 ) 1 \times 1 \times 192 \times 64+(1 \times 1 \times 192 \times 96+3 \times 3 \times 96 \times 128)+(1 \times 1 \times 192 \times 16+5 \times 5 \times 16 \times 32) 1×1×192×64+(1×1×192×96+3×3×96×128)+(1×1×192×16+5×5×16×32)
如果去掉网络中的 1 × 1 1 \times 1 1×1的模块，参数量如下： 1 × 1 × 192 × 64 + 3 × 3 × 192 × 128 + 5 × 5 × 192 × 32 1 \times 1 \times 192 \times 64+3 \times 3 \times 192 \times 128+5 \times 5 \times 192 \times 32 1×1×192×64+3×3×192×128+5×5×192×32由此可见，如果去掉网络中的 1 × 1 1 \times 1 1×1模块，参数量将增加到原来网络的三倍
3.2.3 辅助分类器
辅助分类器在训练的过程中同样会计算损失，在GoogLeNet论文中，辅助分类器的损失被乘以0.3后加到主分类器的损失中作为最终的损失来训练网络，主分类器的结果如下：
辅助分类器的结构如下：
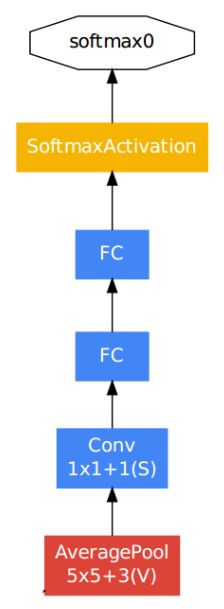
结构的细节具体说来：
- 均值池化层核尺寸为5x5，步长为3；
- 1x1的卷积用于降维，拥有128个滤波器，采用ReLU激活函数；
- 全连接层有1024个神经元，采用ReLU激活函数；
- dropout层的dropped的输出比率为70%；
- softmax激活函数用来分类，和主分类器一样预测1000个类，但在推理时移除。
辅助分类器的作用的是一方面增加了反向传播的梯度信号，帮助低层特征训练，从而低层特征也有很好的区分能力，另一方面辅助分类器提供了额外的正则化效果，对于整个网络的训练很有裨益。
4. ResNet
ResNet是2015年由微软实验室提出的，网络的亮点主要有：
- 超深的网络结构（可以突破1000层）；
- 提出risidual模块：
- 使用batch normalization加速训练（丢弃dropout）；
4.1 网络结构
网络结构如下图所示，其中ResNet为下图中最上层的网络
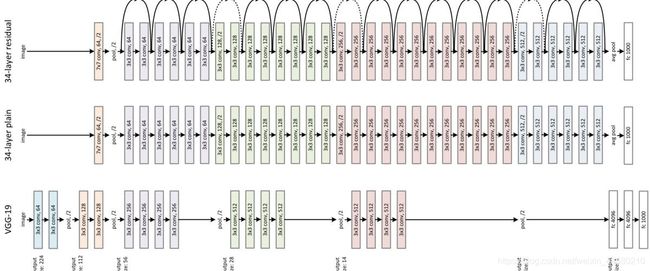
可以看到ResNet其实就是对residual模块的反复堆叠，随着网络层数的增加，深层网络中主要会出现如下两个问题而导致网络效果变差：
- 梯度消失或者梯度爆炸；
- 退化问题；
其中梯度消失或者梯度爆炸主要通过数据预处理、权重初始化以及batch normalization方法解决，而退化问题主要是通过本文提出的residual模块解决，下面分别对这两个关键知识点进行总结。
4.2 关键知识点
4.2.1 residual模块
residual模块主要解决了深层网络出现的退化问题，退化问题具体表现就是层数深的网络反而没有层数浅的好，residual模块结构如下图所示：
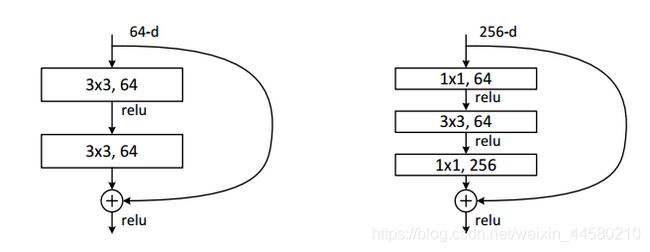
其中，左侧为34层网络的residual模块，右侧为50、101、152层网络的residual模块，右侧residual模块的主要特点是增加 1 × 1 1\times1 1×1卷积核来进行升维和降维，减少网络参数量，以不至于过深的网络带来巨大的参数量导致难以学习。另一个值得注意的点是这里的residual是通过add操作将特征合并，而不是通过concate操作，这里我们来说明下concate操作和add操作的区别：
- add要求整个特征矩阵的长宽和深度都相同，而concate仅仅要求长宽相同，而深度可以不同，因此concate就是按照深度方向进行拼接的
- add和concate操作是可以相互转换的，如下图所示：
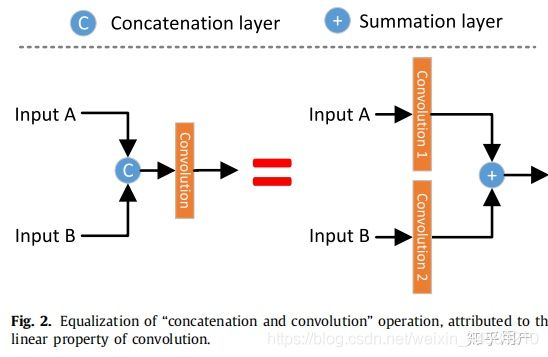
由此可见，add其实可以相当于concate之后对应通道共享同一个卷积核，add相当于加了一种先验，当两路输入可以具有“对应通道的特征图语义类似”（可能不太严谨）的性质的时候，可以用add来替代concate，这样更节省参数和计算量（concate是add的2倍）。
4.2.2 batch normalization
batch normalization是2015年的论文《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》提出的，其目的是使得我们同一通道的feature map满足均值为0，方差为1的分布规律，batch normalization的具体操作如下：假设小批量输入为 B = { x 1 … m } \mathcal{B}=\left\{x_{1 \ldots m}\right\} B={ x1…m}，学习的参数为 γ , β \gamma, \beta γ,β，那么操作主要有如下四个步骤：
- 求得小批量数据的均值： μ B ← 1 m ∑ i = 1 m x i \mu_{\mathcal{B}} \leftarrow \frac{1}{m} \sum_{i=1}^{m} x_{i} μB←m1i=1∑mxi
- 求得小批量数据的方差： σ B 2 ← 1 m ∑ i = 1 m ( x i − μ B ) 2 \sigma_{\mathcal{B}}^{2} \leftarrow \frac{1}{m} \sum_{i=1}^{m}\left(x_{i}-\mu_{\mathcal{B}}\right)^{2} σB2←m1i=1∑m(xi−μB)2
- 进行归一化操作： x ^ i ← x i − μ B σ B 2 + ϵ \widehat{x}_{i} \leftarrow \frac{x_{i}-\mu_{\mathcal{B}}}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}} x i←σB2+ϵxi−μB
- 进行尺度为位移变换： y i ← γ x ^ i + β ≡ B N γ , β ( x i ) y_{i} \leftarrow \gamma \widehat{x}_{i}+\beta \equiv \mathrm{BN}_{\gamma, \beta}\left(x_{i}\right) yi←γx i+β≡BNγ,β(xi)
其中batch normalization的结果为 { y i = B N γ , β ( x i ) } \left\{y_{i}=\mathrm{BN}_{\gamma, \beta}\left(x_{i}\right)\right\} { yi=BNγ,β(xi)}具体操作可以如下图所示：
这里值得注意的是:
- γ , β \gamma, \beta γ,β两个参数是在反向传播过程中学习得到的，在正向推理时是固定的；
-
- 在训练过程中，batch size要尽可能设置得大一些，这样batch normalization层才更加容易学到数据分布规律，并且batch；
- batch normalization层通常放在卷积层和激活层之间，且卷积层不需要设置bias，因此有batch normalization层的话卷积层有无bias的结果是一致的。
5. ResNeXt
ResNeXt是ResNet与Inception的结合体，利用分组卷积的形式在没有增加参数数量的前提下降低了错误率
5.1 网络结构
其网络结构与ResNet类似，都是通过模块堆叠而成，唯一的区别是堆叠的模块不同，如下图所示：
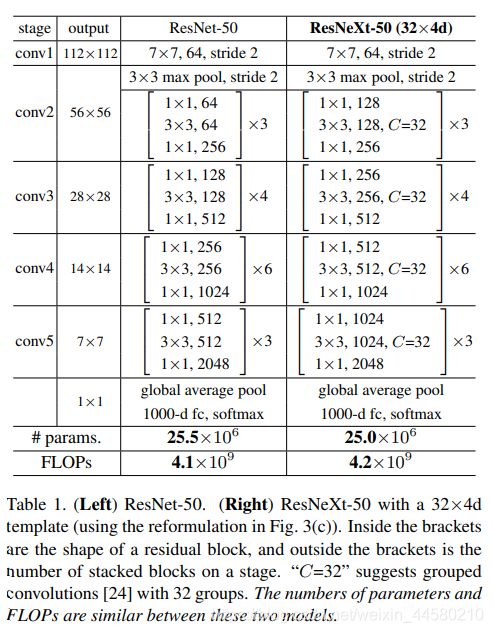
注意到，在参数数量接近的前提下，ResNeXt中的residual模块的通道数要比ResNet多，网络的表达能力相应更强。
5.2 关键知识点
5.2.1 分组卷积
ResNeXt中堆叠的模块本质就是就是采用分组卷积的residual模块，因此首先我们来了解下分组卷积，如下图所示为标准卷积操作：
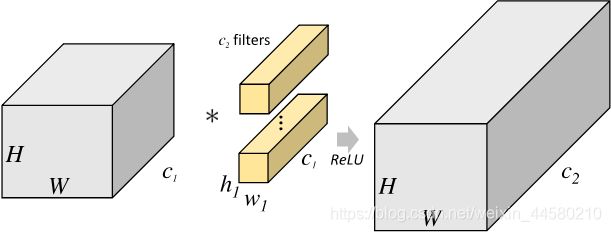
对应卷积层的参数数量为： ( h 1 × w 1 × c 1 ) × c 2 \left({h}_{1} \times {w}_{1} \times {c}_{1}\right) \times {c}_{2} (h1×w1×c1)×c2而分组卷积操作图示如下，将输入按照通道分组后进行卷积后在进行Concate操作：
对应的卷积层参数数量为： h 1 × w 1 × ( c 1 g ) × ( c 2 g ) × g = h 1 × w 1 × c 1 × c 2 × 1 g h_{1} \times w_{1} \times\left(\frac{c_{1}}{g}\right) \times\left(\frac{c_{2}}{g}\right) \times g={h}_{1} \times {w}_{1} \times c_{1} \times c_{2} \times \frac{ {1}}{ {g}} h1×w1×(gc1)×(gc2)×g=h1×w1×c1×c2×g1因此，分组卷积的数量是标准卷积的 1 g \frac{ {1}}{ {g}} g1
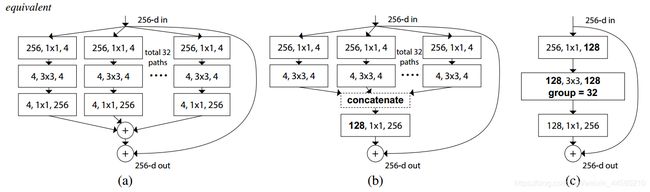
ResNeXt论文中首先提出的是上图中(a)的形式，通过一系列等价变换，最终可以得到如图©所示分组卷积的形式
6. MobileNet
MobileNet目前一共有三个版本，分别是MoblileNet V1, MobileNet V2和MOblieNet V3:
MobileNet V1网络是2017年google团队在2017年提出的，在准确率小幅度降低的前提下大大减少模型参数和运算量，网络的主要亮点有：
- 采用Depthwise Separable Convolution（可分卷积），大大减少了运算量和参数量；
- 增加了控制卷积核卷积个数的超参数 α \alpha α和输入图像大小的 β \beta β；
MobileNet V2网络是2018年google团队在2018年提出的，相比Mobile V1网络准确率更高，模型更小，网络的亮点主要有：
- 采用了Inverted Residual Block（倒残差结构）；
- 采用了Linear Bottlenecks结构；
MoblieNet V3网络在V2的基础上进一步减少了计算量和提高了精度，网路的主要两点如下：
- 采用了bneckj结构，即进一步优化了Inverted Residual Block；
- 使用了Neural Architecture Search搜索参数；
- 重新设计了耗时层结构 ；
6.1 网络结构
MobileNet V1的网络结构与VGG类似，结构如下所示：
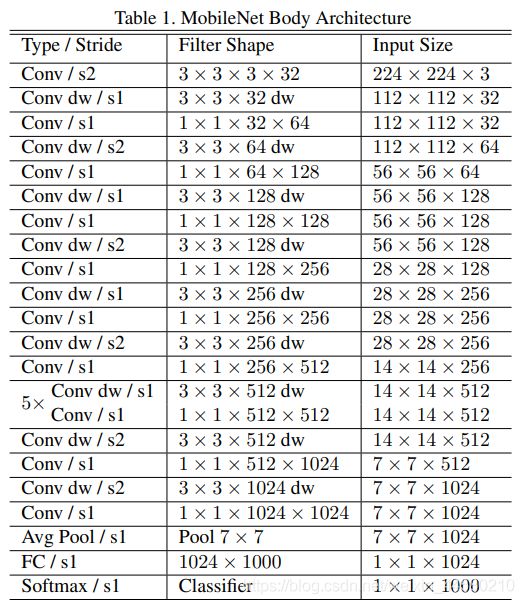
其中Conv dw指的就是Depthwise Separable Convolution，下文介绍
MobileNet V2的网路结构如下所示：
其中bottleneck指的就是Inverted Residual Block和Linear Bottleneck结构。
MobileNet V3中后面涉及到这一部分工作的时候再详读论文进行补充。
6.2 关键知识点
6.2.1 Depthwise Separable Convolution
Depthwise Separable Convolution即深度可分卷积，传统卷积如下图所示：
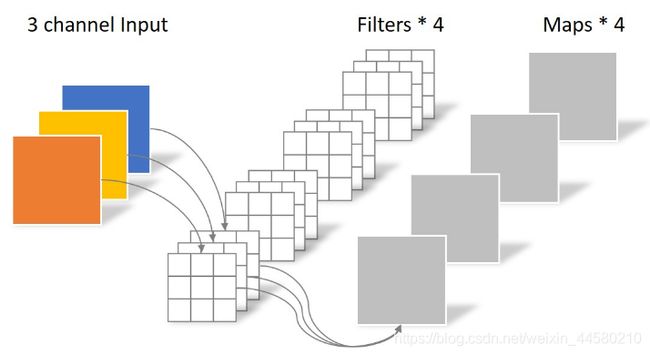
而Depthwise Separable Convolution由两部分组成，分别是Depthwise Convolution和Pointwise Convolution，其中Depthwise Convolution操作如下图所示：
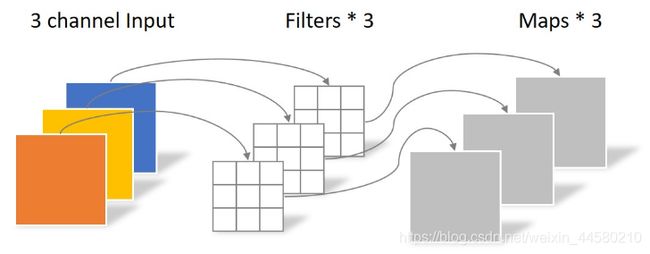
Pointwise Convolution操作如下图所示：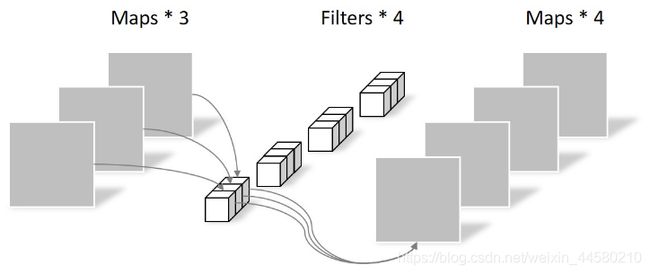
假设输入矩阵维度为 D K × D K × M D_K \times D_K \times M DK×DK×M，卷积核大小为 D F × D F × M D_F \times D_F \times M DF×DF×M，数量为 N N N，因此普通卷积计算量为 D K ⋅ D K ⋅ M ⋅ N ⋅ D F ⋅ D ˉ F D_{K} \cdot D_{K} \cdot M \cdot N \cdot D_{F} \cdot \bar{D}_{F} DK⋅DK⋅M⋅N⋅DF⋅DˉF可分卷积计算量为： D K ⋅ D K ⋅ M ⋅ D F ⋅ D F + M ⋅ N ⋅ D F ⋅ D F D_{K} \cdot D_{K} \cdot M \cdot D_{F} \cdot D_{F}+M \cdot N \cdot D_{F} \cdot D_{F} DK⋅DK⋅M⋅DF⋅DF+M⋅N⋅DF⋅DF因此理论上普通卷积计算量是可分卷积的8到9倍。在实验过程中发现Depthwise Convolution参数大部分为零，这是不合理的，在MobileNet V2网络中对这个问题有所优化
6.2.2 Inverted Residuals Block 和 Linear Bottleneck
在ResNet中提出了Residual Block模块，如下图所示：
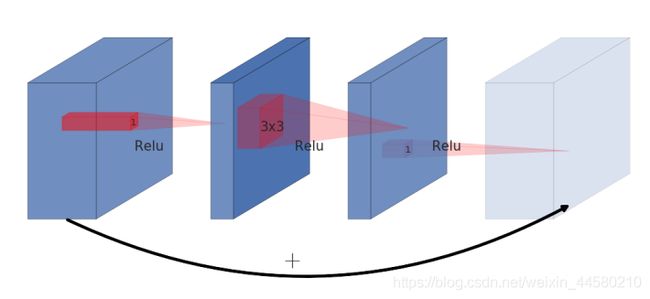在该“两头大中间小“的结构中，步骤如下：
- 1 × 1 1 \times 1 1×1卷积降维；
- 3 × 3 3 \times 3 3×3标准卷积；
- 1 × 1 1 \times 1 1×1卷积升维；
而在Inverted Residual Block模块的结构如下图所示：
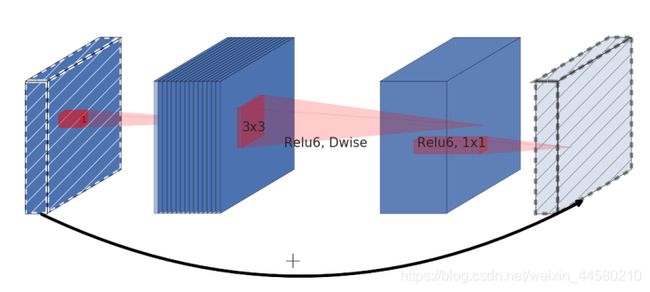
具体步骤如下：
- 1 × 1 1 \times 1 1×1卷积升维
- 3 × 3 3 \times 3 3×3Depthwise Separable Convolution
- 1 × 1 1 \times 1 1×1卷积降维
在inverted residual block中使用的Relu6激活函数： y = ReLU 6 ( x ) = min ( max ( x , 0 ) , 6 ) y=\operatorname{ReLU} 6(x)=\min (\max (x, 0), 6) y=ReLU6(x)=min(max(x,0),6)此外，在Inverted Residual Block模块中的最后一个卷积层使用的是线性激活函数，论文中通过实验发现Relu激活函数对低维度特征信息造成大量损失，而Inverted Residual Block中使是"中间大两头小"的结构，因此输出是相对低维度的特征，因此需要使用线性激活函数来替代Relu函数来避免对低维度特征信息造成损失。具体结构如下：
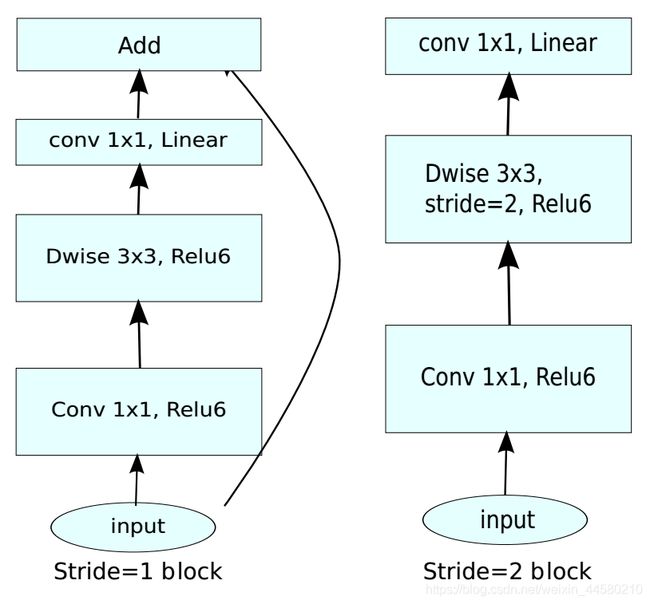
当stride = 1 且输入特征矩阵与输出特征矩阵shape相同时才有shortcut连接
7. ShuffleNet
ShuffleNet有两个版本，ShuffleNet V1网络的特点主要如下：
- 提出了Channel Shuffle的思想；
- ShuffleNet V1中采用的全是Group Convolution和Depthwise Separable Convolution。
ShuffleNet V2网络中提出了四条高效网络设计准则：
- Equal Channel width minimizes memory access cost(MAC)；
- Excessive group convolution increases MAC；
- Network fragmentation reduces degree of parallelism;
- Element-wise operations are non-negligible
并基于这四条准则重新优化了网络结构，ShuffleNet V2相对硬核，有很多有意义的实验，这里仅仅总结Shuffle V1中的知识点，以后工作中设计到Shuffle V2要使用的相关知识在去仔细读读论文。
7.1 网络结构
ShuffleNet V1的网络结构如下：
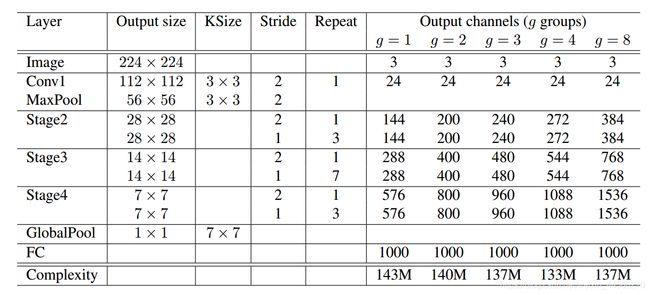
从网络结构看，仍然是模块的堆叠，但是不同的是，在ShuffleNet V1中采用的全部都是Group Convolution和Depthwise Separable Convolution，如下图所示：
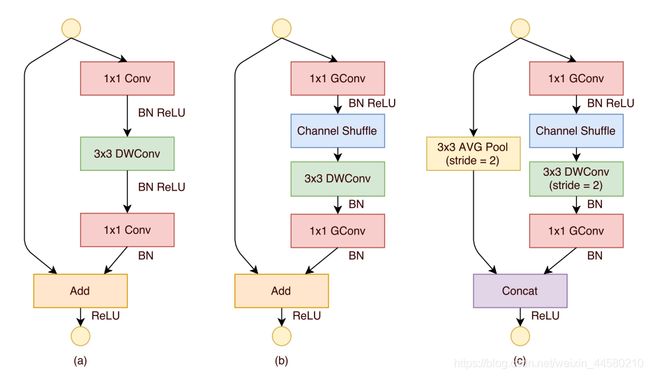
上图中(a)是ResNeXt中的卷积结构，计算量为： h w ( 1 × 1 × c × m ) + h w ( 3 × 3 × m × m ) / g + h w ( 1 × 1 × m × c ) = h w ( 2 c m + 9 m 2 / g ) h w(1 \times 1 \times c \times m)+h w(3 \times 3 \times m \times m) / g+h w(1 \times 1 \times m \times c)=h w\left(2 c m+9 m^{2} / g\right) hw(1×1×c×m)+hw(3×3×m×m)/g+hw(1×1×m×c)=hw(2cm+9m2/g)图(b)和图©分别是stride=1和stride=2的ShuffleNet V1中的结构，我们计算图(b)的计算量为： h w ( 1 × 1 × c × m ) / g + h w ( 3 × 3 × m ) + h w ( 1 × 1 × m × c ) / g = h w ( 2 c m / g + 9 m ) h w(1 \times 1 \times c \times m) / g+h w(3 \times 3 \times m)+h w(1 \times 1 \times m \times c) / g=h w(2 c m / g+9 m) hw(1×1×c×m)/g+hw(3×3×m)+hw(1×1×m×c)/g=hw(2cm/g+9m)由此可见ShuffleNet中计算量会小很多。
7.2 关键知识点
7.2.1 Channel Shuffle思想
ResNeXt网络中使用的Group Convolution虽然可以减少参数与计算量，但是Group Convolution中不同组之间的信息没有交流，那么Channel Shuffle的基本思想就如下图所示：
具体说来，就是将经过第一次Group Convolution之后的结果，将不同Group间的Channel混乱后再进行第二次Group Convolution
8. EfficientNet
这篇文论是google在2019年发表的文章，文章同事探讨了输入分辨率，网路分辨率和宽度的影响：
- 增加网络的深度，能够得到更加丰富、复杂的特征并且能够很好的应用到其他任务中，但网络的深度过深会面临梯度消失，训练困难的问题。
- 增加网络的宽度，能够过得更高细粒度的特征并且也更容易训练，但对于width很大而深度较浅的网络往往很难学习到更加深层次的特征。
- 增加输入网络的图像分辨率能够获得更高细粒度的特征模板，但对于非常高的输入分辨，准确率增加的收益会减小，并且大分辨率图像会增加计算量。具体影响如下图所示：
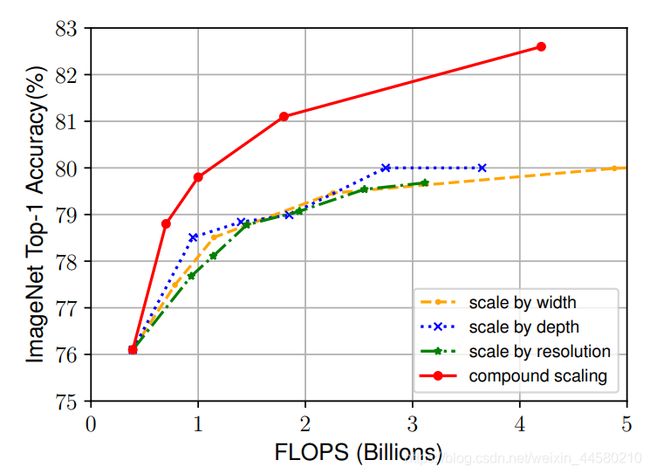
EfficeintNet中的网络结构与MobileNet V3中相似，这一部分内容后面在进行补充
总结
这篇博客我流水账式地总结了一些经典的网络框架，MobileNet V3、ShuffleNet V2和EfficintNet网络应该都是高效网络设计的较新的成果，这三个网络框架我之后再详读论文进行补充。