纯小白的机器学习之路(一):使用OpenCV提供的kNN模型实现简单类别的预测
写在最前
其实从寒假我就开始接触python和机器学习,资料是看了一大堆,但是总觉得真到了应用的时候还是一窍不通,况且一段时间过去就忘个一干二净。学编程像高中那样记笔记总归是不大行,于是我想到了写csdn博客,把我所理解的东西写出来,算是应用了一遍知识,也作为我的笔记吧。我还只是个卑微本科生,也是第一次写技术类文章,搞出来的东西必然有疏漏,还请您各位多包涵。
什么是kNN算法?
kNN(k-Nearest Neighbour),即k-最近邻算法,是数据分类算法中最简单的方法之一。很多纸质书籍和网上教程都把它放在第一章来讲述(至少我看到的是这样),所以我也把kNN作为我机器学习的第一步。它的大概流程是这样:
1. 计算测试数据到各个训练数据之间的距离,即:
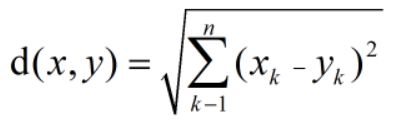
2. 将计算得到的距离进行排序
3. 选取距离最小的k个点
4. 判断这k个点所在类别的频率
5. 返回频率最高的类别作为预测结果
我找到的几个教程,要么压根不讲kNN的原理,直接教你调用;要么只给一个数学描述,你自己慢慢揣摩去吧。这对像我一样又菜又爱刨根究底的人来说未免太不友好。迈克尔·麦耶勒博士在解释kNN时,举了一个例子用于实战,我在这里加以改编(紧 跟 时 事):
蓝星上有个大漂亮国,他们的最高领袖被称为漂亮国大统领。在建国之初人们就约定,以选举的方式选出大统领,四年一届,最多连任两届。0202年,又到了漂亮国的大选年。由于现任大统领川最懂的迷之操作,漂亮国全社会面临着空前的分裂。按照惯例,有两个党派将参与大统领的竞争:象党(红色三角形)和驴党(蓝色正方形)。我们假设有一个小镇,民众间的意见极为不统一,以至于两党的支持者都不愿意做彼此的邻居。现在,有个小老板想搬入这个镇子,我们能否通过他居住的地点(即他的邻居)来判断他是哪一党的支持者呢?
(注:以下代码均用Jupyter Notebook实现)
首先引用必需的库
import numpy as np
import cv2
import matplotlib.pyplot as plt
由于这是一个完全虚拟的情景,所以训练数据(即小镇上的原住民)需要我们自己生成。我们将小镇的地图视作一个二维的直角坐标系,那么一个数据应该包含三个元素:x坐标,y坐标,以及居住在此位置居民的类别(支持哪一派)。我们用如下的一个函数来生成训练数据:
np.random.seed(42)
# 通过在地图上随机选取一个位置并随机分配一个标签
# 0为蓝色正方形,1为红色三角形
def generate_data(num_samples, num_features=2): # num_features表示所需的数据点都有两个特征
data_size = (num_samples, num_features)
data = np.random.randint(0, 100, size=data_size)
# 创建一个数据矩阵,它有num_samples行,num_features列
labels_size = (num_samples,1)
labels = np.random.randint(0, 2, size=labels_size)
# 创建一个含有标签的向量(0和1)
return data.astype(np.float32),labels
# OpenCV对数据类型有些特殊的要求,所以确保把数据点数据类型转为
# float32
生成一些训练数据
train_data, labels = generate_data(11)
输出train_data,可以看到它现在是一个矩阵。
array([[71., 60.],
[20., 82.],
[86., 74.],
[74., 87.],
[99., 23.],
[ 2., 21.],
[52., 1.],
[87., 29.],
[37., 1.],
[63., 59.],
[20., 32.]], dtype=float32)
现在我们将上述训练数据画在地图上,方便接下来的理解。
def plot_data(all_blue, all_red):
plt.scatter(all_blue[:, 0], all_blue[:, 1], c='b', marker='s', s=180)
plt.scatter(all_red[:, 0], all_red[:, 1], c='r', marker='^', s=180)
plt.xlabel('x coordinate')
plt.ylabel('y coordinate')
blue = train_data[labels.ravel() == 0] # 对应标签为0的即为蓝色数据点
red = train_data[labels.ravel() == 1] # 对应标签为1的即为红色数据点
plot_data(blue, red)
结果如图:
现在我们就可以训练分类器了,这里我利用OpenCV的ml模块创建一个分类器,并传入训练数据:
knn = cv2.ml.KNearest_create()
knn.train(train_data, cv2.ml.ROW_SAMPLE, labels)
传入训练数据成功后,knn.train函数会返回True。
我们利用上面的generate_data函数生成一个新的数据点,把它当作新搬来的小老板。
newcomer, _ = generate_data(1) # 函数将返回一随机的类别,用一个下划线忽略该返回值,因为我们将预测它是何值
新的数据点内容为:
array([[91., 59.]], dtype=float32)
我们也把它画在小镇地图上,用绿色圆形表示:
plot_data(blue, red)
plt.plot(newcomer[0, 0], newcomer[0, 1], 'go', markersize=14)

其实这时候,如果给你一个k值,你自己就可以预测绿色点的类别,但是随着k值的增大,人工判断可能会变得越来越困难。用kNN的findNearest方法可以预测新数据点的类别:
# 从图中就可看出,k=1时,最近邻是红色三角形
ret, result, neighbour, distance = knn.findNearest(newcomer, 1)
print('Predicted Result:\t', result)
print('Neighbour result:\t', neighbour)
print('Neighbour distance:\t', distance)
结果为:
Predicted Result: [[1.]]
Neighbour result: [[1.]]
Neighbour distance: [[250.]]
findNearest方法给出了计算得到的距离。k=1时,最近邻的距离为250单位,它的类别是红色三角形,那么预测的结果也是红色三角形。当设置k=2或3时,预测的结果也一样。
如果我们扩大k值,比如令k=7:
ret, result, neighbour, distance = knn.findNearest(newcomer, 7)
print('Predicted Result:\t', result)
print('Neighbour result:\t', neighbour)
print('Neighbour distance:\t', distance)
结果为:
Predicted Result: [[0.]]
Neighbour result: [[1. 1. 0. 0. 0. 1. 0.]]
Neighbour distance: [[ 250. 401. 784. 916. 1073. 1360. 4885.]]
可以发现,预测的类型发生了变化(蓝色正方形)。在最近邻范围内,有四个蓝色正方形,三个红色三角形,因此分类器将新来者预测为蓝色正方形。
由此可见,kNN的预测结果很可能会随着k值的变化而变化。大多数情况下,
我们无法提前知道最佳的k值选择,通常做法是使用交叉验证(Cross Validation)来寻找一个最适合的k值,然而这就涉及到我的知识盲区了。
总结
其实结合着这个例子和图表来看,kNN算法确实非常容易理解,我们甚至可以手写一个kNN算法实现与第三方库中的API同样的功能。它的应用也是极为广泛的。比如我们更改一下上面的例子,将象党驴党改成良性肿瘤和恶性肿瘤,横纵轴改为与之相关的因素,就可以实现简单而粗糙的机器肿瘤判断。