深度学习进阶NLP：word2vec的高速化

关注“深度学习冲鸭”，一起学习一起冲鸭！

设为星标，第一时间获取更多干货

编辑：王萌

word2vec的高速化

上一篇我们讲到了在神经网络中词向量的表示方法：最著名的就是word2vec，并且实现了CBOW模型的代码。想要回顾的可以看这里师妹问我：如何在7分钟内彻底搞懂word2vec？

word2vec虽然简单，但是的确存在一些问题，比如随着语料库中词汇量的增加，计算量也随之增加。当词汇量达到一定程度之后， CBOW 模型的计算就会花费过多的时间。

因此，本节将对 word2vec 进行加速。

两点改进：

• 引入名为Embedding 层（嵌入层）的新层；

• 引入名为 Negative Sampling（负采样） 的新损失函数。

改进之后，我们会在 PTB 数据集上进行学习，实际评估一下所获得的单词的分布式表示的优劣。

先回顾一下上一节的简单CBOW模型：

数据在模型中的传递步骤如下：

1. 接收 2 个单词的上下文，以预测目标词的概率；

2. 输入层和输入侧权重（Win）之间的矩阵乘积计算出中间层；

3. 中间层和输出侧权重（Wout）之间的矩阵乘积计算每个单词的得分；

4. 这些得分经过Softmax函数，得到每个单词的出现概率；

5. 将这些概率与正确解标签进行比较（使用交叉熵误差函数进行对比），从而计算出损失；

6. 再将损失值通过反向传播给前向网络，进行权重Win的更新，重新回到步骤1进行迭代；

7. 不断迭代更新权重，直到交叉熵误差的损失值小到你的要求，就停止迭代，得到最终的权重值，也就是词向量。

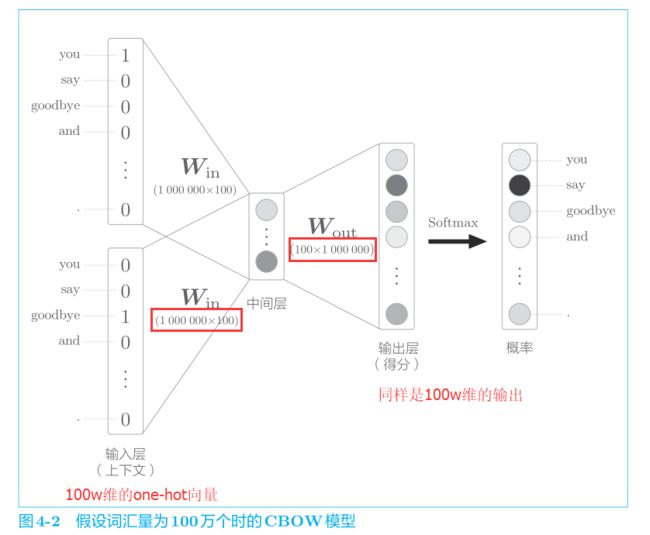
这个时候，语料库还很小，模型还hold得住。但是现实生活中可没这么理想。假设词汇量有 100 万个，CBOW 模型的中间层神经元有 100 个，那么

这中间的计算过程需要很长时间，比如

1. 输入层的 one-hot 表示和权重矩阵 Win 的乘积

2. 中间层和权重矩阵 Wout 的乘积以及 Softmax 层的计算

结论先行。

对于问题一，通过引入新的 Embedding 层来解决；

对于问题二，通过引入 Negative Sampling 这一新的损失函数来解决。

代码：

改进前的 word2vec 实现在 ch03/ simple_cbow.py（或 者 simple_skip_gram.py）中。

改进后的 word2vec 实现在 ch04/ cbow.py（或者 skip_gram.py）中。

word2vec的改进一：引入Embedding 层

我们把输入层的 one-hot 表示和权重矩阵 Win 的乘积这一个计算单独拿出来看看它究竟做了什么。我们知道根据简单的CBOW模型就是矩阵乘积，但是从图中我们可以发现，其实它就是把单词one-hot为1的对应权重矩阵Win的行（向量）抽取出来了。因此，矩阵乘积没有必要。

于是我们可以创建一个从权重参数中抽取“单词 ID 对应行（向量）”的层，称之为 Embedding 层。顺便说一句，Embedding 来自“词嵌入”（word embedding）这一术语。也就是说，在这个 Embedding 层存放词嵌入（分布式表示）。

Embedding 的代码实现

从矩阵中取出某一行的处理是很容易实现的。假设权重 W 是二维数组。如果要从这个权重中取出某个特定的行，只需写 W[2]或者 W[5]（取出第二行或第五行）。用 Python 代码来实现，如下所示。

>>> import numpy as np
>>> W = np.arange(21).reshape(7, 3)
>>> W
array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11],
       [12, 13, 14],
       [15, 16, 17],
       [18, 19, 20]])
>>> W[2]
array([6, 7, 8])


>>> W[5]
array([15, 16, 17])

一次性提取多行的处理也很简单，只需通过数组指定行号即可。

>>> idx = np.array([1, 0, 3, 0])
>>> W[idx]
array([[ 3,  4,  5],
       [ 0,  1,  2],
       [ 9, 10, 11],
       [ 0,  1,  2]])

  正向传播

下面，我们来实现 Embedding 层的 forward() 方法。假定用于mini-batch 处理。（common/layers.py）。

class Embedding:
    def __init__(self, W):
        self.params = [W]
        self.grads = [np.zeros_like(W)]
        self.idx = None  # idx中以数组的形式保存需提取的行索引（单词 ID）
        
    def forward(self, idx):
        W, = self.params
        self.idx = idx
        out = W[idx]
        return out

  反向传播

Embedding 层的正向传播只是从权重矩阵 W 中提取特定的行，并将该特定行的神经元原样传给下一层。因此，在反向传播时，从上一层（输出侧的层）传过来的梯度将原样传给下一层（输入侧的层）。不过，从上一层传来的梯度会被应用到权重梯度 dW 的特定行（idx），如图 4-4 所示。

因此，反向传播backward()代码如下：

def backward(self, dout):
    dW, = self.grads
    dW[...] = 0
    dW[self.idx] = dout # 不太好的方式
    return None

这里，取出权重梯度 dW，通过 dW[...] = 0 将 dW 的元素设为 0（并不是将 dW 设为 0，而是保持 dW 的形状不变，将它的元素设为 0）。然后，将上一层传来的梯度 dout 写入 idx 指定的行。

但是在 idx 的元素出现重复时，会出现问题。比如，当 idx 为 [0, 2, 0, 4] 时，就会发生图 4-5中的问题。

如图 4-5 所示，我们将 dh 各行的值写入 dW 中 idx 指定的位置。在这种情况下，dW 的第 0 行会被写入两次。这样一来，其中某个值就会被覆盖掉。为了解决这个重复问题，需要进行“加法”，而不是“写入”（请读者考虑一下为什么是加法）。也就是说，应该把 dh 各行的值累加到 dW 的对应行中。下面，我们来实现正确的反向传播。

def backward(self, dout):
    dW, = self.grads
    dW[...] = 0
    for i, word_id in enumerate(self.idx):  # 使用 for 循环将梯度累加到对应索引上
        dW[word_id] += dout[i]
    # 或者
    # np.add.at(dW, self.idx, dout)  # np.add.at(A, idx, B) 将B加到A上，idx指定A中需进行加法的行。
    return None

通常情况下，NumPy 的内置方法比 Python 的 for循环处理更快。这是因为 NumPy 的内置方法在底层做了高速化和提高处理效率的优化。因此，上面的代码如果使用 np.add.at()来实现，效率会比使用 for循环处理高得多。

关于 Embedding 层的改进就介绍到这里。现在，我们可以将 word2vec（CBOW 模型）的实现中的输入侧的 MatMul 层换成 Embedding 层。这样一来，既能减少内存使用量，又能避免不必要的计算。

word2vec的改进二：引入新损失函数：负采样

word2vec 的另一个瓶颈在于中间层之后的处理，即矩阵乘积和 Softmax 层的计算。

这里我们采用负采样（negative sampling）的方法来解决。使用 Negative Sampling 替代 Softmax，无论词汇量有多大，都可以使计算量保持较低或恒定。

如图 4-6 所示，输入层和输出层有 100 万个神经元。在上一节中，我们通过引入 Embedding 层，节省了输入层中不必要的计算。剩下的问题就是中间层之后的处理。此时，在以下两个地方还需要很多计算时间。

• 中间层的神经元和权重矩阵（Wout）的乘积

• Softmax 层的计算

  什么是负采样？

负采样：这个方法的关键思想在于用二分类（binary classification）去拟合多分类（multiclass  classification），这是理解负采样的重点。

上述问题中，我们处理的都是多分类问题。拿刚才的例子来说，我们把它看作了从 100 万个单词中选择 1 个正确单词的任务。那么，可不可以将这个问题处理成二分类问题呢？更确切地说，我们是否可以用二分类问题来拟合这个多分类问题呢？

二 分 类 处 理 的 是 答 案 为“Yes/No”的 问 题。诸 如，“这个数字是7 吗？”“这 是 猫 吗？”“目 标 词 是 say 吗？”等，这 些 问 题 都 可 以 用“Yes/No”来回答。

对于“当上下文是 you 和 goodbye 时，目标词是什么？”这个问题，神经网络可以给出正确答案。

现在，我们来考虑如何将多分类问题转化为二分类问题。为此，我们先考察一个可以用“Yes/No”来回答的问题。比如，让神经网络来回答“当上下文是 you 和 goodbye 时，目标词是 say 吗？”这个问题，这时输出层只需要一个神经元即可。可以认为输出层的神经元输出的是 say 的得分。

如图 4-7 所示，输出层的神经元仅有一个。因此，要计算中间层和输出侧的权重矩阵的乘积，只需要提取 say 对应的列（单词向量），并用它与中间层的神经元计算内积即可。这个计算的详细过程如图 4-8 所示。

如图 4-8 所示，输出侧的权重 Wout 中保存了各个单词 ID 对应的单词向量。此处，我们提取 say 这个单词向量，再求这个向量和中间层神经元的内积，这就是最终的得分。

原来输出层是以全部单词为对象进行计算的。这里，我们仅关注单词 say，计算它的得分。然后，使用 sigmoid 函数将其转化为概率。

在多分类的情况下，输出层使用Softmax 函数将得分转化为概率，损失函数使用交叉熵误差。

在二分类的情况下，输出层使用sigmoid 函数，损失函数也使用交叉熵误差。

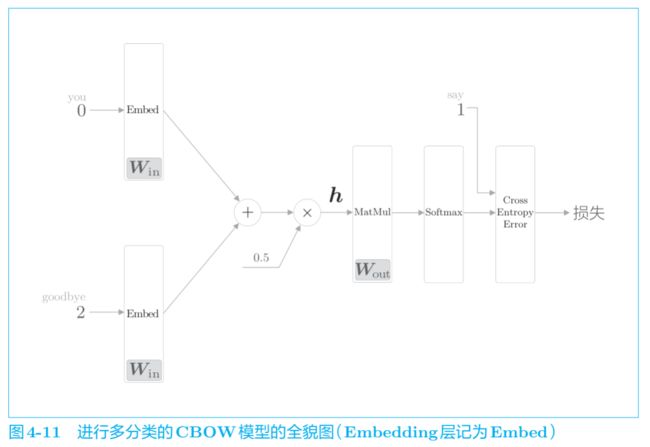
下面我们从层的角度来看看CBOW模型：

多分类

二分类

当答案是“Yes”时，向 Sigmoid with Loss 层输入 1。

当答案是“No”时，向 Sigmoid with Loss 层输入 0。

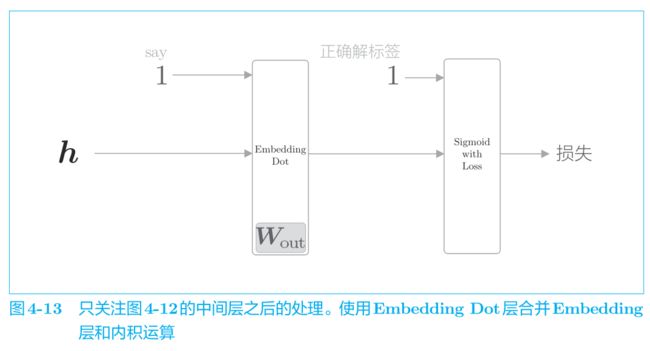
为了便于理解模型后半部分，我们把它单独拧出来看，且将图 4-12 中的 Embedding 层和 dot运算（内积）合并起来处理，可以简化成图 4-13。

Embedding Dot 层的实现

class EmbeddingDot:
    def __init__(self, W):
        self.embed = Embedding(W)  # 保存 Embedding 层
        self.params = self.embed.params  # 保存参数
        self.grads = self.embed.grads  # 保存梯度
        self.cache = None  # 保存正向传播时的计算结果
        
    def forward(self, h, idx):  # idx是单词ID列表，通过idx实现mini-batch处理，得出Wout
        target_W = self.embed.forward(idx)
        out = np.sum(target_W * h, axis=1)  # axis=1表示按第一维度，也就是按行进行求和
        self.cache = (h, target_W)
        return out
    
    def backward(self, dout):
        h, target_W = self.cache
        dout = dout.reshape(dout.shape[0], 1)
        dtarget_W = dout * h
        self.embed.backward(dtarget_W)
        dh = dout * target_W
        return dh

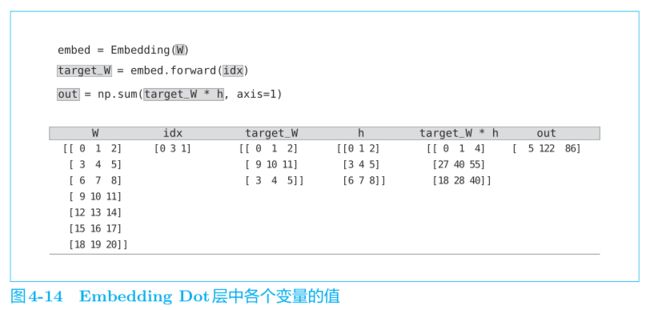
我们用具体值来举个例子：

idx=[0 3 1] 表示取第0行、3行和1行。（实现mini-batch处理，同时处理提高效率）

target_W * h 表示内积，也就是对应元素相乘。

out 表示对结果逐行（axis=1）进行求和。

以上就是对 Embedding Dot 层的正向传播的介绍。反向传播以相反的顺序传播梯度，这里我们省略对其实现的说明（并不是特别难，请大家自己思考）。

  负采样

至此，我们实现了多分类转化为二分类问题，问题就解决了嘛？不是的。如上所述，我们只考虑了正确解“say”，而没有考虑错误解的情况。也就是说，我们目前仅学习了正例（正确答案），还不确定负例（错误答案）会有怎样的结果。

如果此时模型有“好的权重”，则 Sigmoid 层的输出（概率）将接近 1。

当前的神经网络只是学习了正例 say，但是对 say 之外的负例一无所知。而我们真正要做的事情是，对于正例（say），使 Sigmoid 层的输出接近 1；对于负例（say 以外的单词），使 Sigmoid 层的输出接近 0。

比如，当上下文是 you 和 goodbye 时，我们希望目标词是 hello（错误答案）的概率较低。也就是越接近0越好。

为了把多分类问题处理为二分类问题，对于“正确答案”（正例）和“错误答案”（负例），都需要能够正确地进行分类（二分类）。因此，需要同时考虑正例和负例。

但是除去say以外的词都是负例，我们都需要考虑嘛？肯定不是啊！那样就违背了我们想解决计算量大这个问题的初衷。所以我们会用近似的方法，选择若干个（5 个或者 10 个）负例去计算。这就是负采样方法的含义。

最后，将正例和采样出来的负例的损失加起来就是最终的损失。

  负采样的采样方法

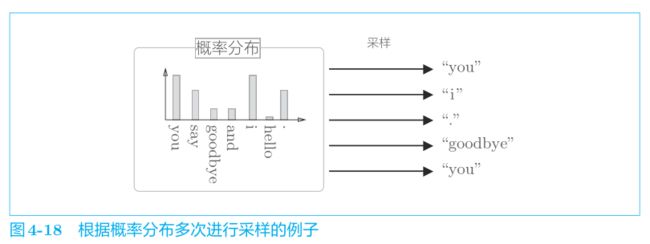
那么如何抽取负例呢？基于语料库的统计数据进行采样的方法比随机抽样要好。也就是说，语料库中经常出现的单词容易被抽到，语料库中不经常出现的单词难以被抽到。

基于语料库中各个单词的出现次数求出概率分布后，只需根据这个概率分布进行采样就可以了。

处理稀有单词的重要性较低。相反，处理好高频单词才能获得更好的结果。

下面，我们使用 Python 来实现基于概率分布的采样。可以使用NumPy 的 np.random.choice() 方法进行采样。

# 基于概率分布进行采样
>>> words = ['you', 'say', 'goodbye', 'I', 'hello', '.']
>>> p = [0.5, 0.1, 0.05, 0.2, 0.05, 0.1]
>>> np.random.choice(words, p=p)
'you'

word2vec 中提出的负采样对刚才的概率分布增加了一个步骤。如式 (4.4)所示，对原来的概率分布取 0.75 次方。

P(wi) 表示第 i 个单词的概率。式 (4.4) 只是对原来的概率分布的各个元素取 0.75 次方。为了使变换后的概率总和仍为 1，分母需要变成“变换后的概率分布的总和”。

为什么这么做呢？这是为了防止低频单词被忽略。通过取 0.75 次方，低频单词的概率将稍微变高。我们来看一个具体例子，如下所示。

>>> p = [0.7, 0.29, 0.01]
>>> new_p = np.power(p, 0.75)
>>> new_p /= np.sum(new_p)
>>> print(new_p)
[ 0.64196878  0.33150408  0.02652714]>>> p = [0.7, 0.29, 0.01]
>>> new_p = np.power(p, 0.75)
>>> new_p /= np.sum(new_p)
>>> print(new_p)
[ 0.64196878  0.33150408  0.02652714]

通过这种方式，使得低频单词稍微更容易被抽到。此外，0.75 这个值并没有什么理论依据，也可以设置成0.75 以外的值。

因此，负采样的步骤就是：

• 从语料库生成单词的概率分布，在取其 0.75 次方

• 使用 np.random.choice() 对负例进行采样。

具体实现在 ch04/negative_sampling_layer.py 的UnigramSampler 类中。这里仅简单说明UnigramSampler 类的使用方法，具体实现可参考附带代码。

unigram 是“1 个（连 续）单 词”的 意 思。同 样 地，bigram 是“2个 连 续 单 词”的 意 思，trigram 是“3 个 连 续 单 词”的 意 思。这 里使 用 UnigramSampler这 个 名 字，是 因 为 我 们 以 1 个 单 词 为 对 象 创建 概 率 分 布。如 果 是 bigram，则 以 (‘you’, ‘say’)、(‘you’, ‘goodbye’)……这样的 2 个单词的组合为对象创建概率分布。

UnigramSampler 类有 3 个参数，分别是单词 ID 列表格式的 corpus、对概率分布取的次方值 power（默认值是0.75）和负例的采样个数 sample_size。

UnigramSampler 类有 get_negative_sample(target) 方法，该方法以参数 target 指定的单词 ID 为正例，对其他的单词 ID 进行采样。

# 指定三个参数的具体值
corpus = np.array([0, 1, 2, 3, 4, 1, 2, 3])
power = 0.75
sample_size = 2


sampler = UnigramSampler(corpus, power, sample_size)
target = np.array([1, 3, 0])
negative_sample = sampler.get_negative_sample(target)
print(negative_sample)
# [[0 3]
#  [1 2]
#  [2 3]]

这里，将 [1, 3, 0] 这 3 个数据的 mini-batch 作为正例。此时，对各个数据采样 2 个负例。第 1 个数据的负例是 [0, 3]，第 2 个是 [1, 2]，第 3 个是 [2, 3]。这样一来，我们就完成了负采样。

  负采样的实现

接下来我们要实现负采样，我们把它实现为 NegativeSamplingLoss 类。（ch04/negative_sampling_layer.py）。

class NegativeSamplingLoss:
    def __init__(self, W, corpus, power=0.75, sample_size=5):
        self.sample_size = sample_size  # 采样负例的数量
        self.sampler = UnigramSampler(corpus, power, sample_size)
        self.loss_layers = [SigmoidWithLoss() for _ in range(sample_size + 1)]  # sample_size + 1是因为要生成一个正例用的层和 sample_size 个负例用的层
        self.embed_dot_layers = [EmbeddingDot(W) for _ in range(sample_size + 1)]
        self.params, self.grads = [], []
        for layer in self.embed_dot_layers:
            self.params += layer.params
            self.grads += layer.grads    
    
    # 正向传播  
    def forward(self, h, target):  # h=中间层的神经元；target=正例目标词
    batch_size = target.shape[0]
    negative_sample = self.sampler.get_negative_sample(target)  # 使用 self.sampler 采样负例
    
    # 正例的正向传播，假设loss_layers[0] 和 embed_dot_layers[0] 是处理正例的层
    score = self.embed_dot_layers[0].forward(h, target)
    correct_label = np.ones(batch_size, dtype=np.int32) # 正例标签是1
    loss = self.loss_layers[0].forward(score, correct_label)
    
    # 负例的正向传播
    negative_label = np.zeros(batch_size, dtype=np.int32) # 负例标签是0
    for i in range(self.sample_size):
        negative_target = negative_sample[:, i]
        score = self.embed_dot_layers[1 + i].forward(h, negative_target)
        loss += self.loss_layers[1 + i].forward(score, negative_label)
        
    return loss  # 正例、负例的损失和


  # 反向传播，只需要以与正向传播相反的顺序调用各层的backward()函数即可
    def backward(self, dout=1):
        dh = 0
        for l0, l1 in zip(self.loss_layers, self.embed_dot_layers):
            dscore = l0.backward(dout)
            dh += l1.backward(dscore)
        return dh

改进版word2vec的学习

到目前为止，我们首先实现 Embedding层，又实现了负采样。现在我们进一步来实现进行了这些改进的神经网络，并在 PTB 数据集上进行学习，以获得更加实用、真实的单词的分布式表示。

  CBOW模型的实现

这里，我们将改进上一节的简单的 SimpleCBOW 类，来实现改进版本的 CBOW 模型。改进之处在于使用Embedding 层和 Negative Sampling Loss 层。此外，我们将上下文部分扩展为可以处理任意的窗口大小。

import sys
sys.path.append('..')
import numpy as np
from common.layers import Embedding
from ch04.negative_sampling_layer import NegativeSamplingLoss


class CBOW:
    # 先进行初始化
    def __init__(self, vocab_size, hidden_size, window_size, corpus): #（词汇量，中间层的神经元个数，上下文的大小，单词ID列表）
        V, H = vocab_size, hidden_size
        
        # 初始化权重
        W_in = 0.01 * np.random.randn(V, H).astype('f')
        W_out = 0.01 * np.random.randn(V, H).astype('f')
        
        # 生成层
        self.in_layers = []
        for i in range(2 * window_size):  # 创建2 * window_size个Embedding 层
            layer = Embedding(W_in)  # 使用Embedding层
            self.in_layers.append(layer)
        self.ns_loss = NegativeSamplingLoss(W_out, corpus, power=0.75, sample_size=5)
        
        # 将所有的权重和梯度整理到列表中
        layers = self.in_layers + [self.ns_loss]
        self.params, self.grads = [], []
        for layer in layers:
            self.params += layer.params
            self.grads += layer.grads
            
        # 将单词的分布式表示W_in设置为成员变量
        self.word_vecs = W_in
    # 正向传播    
    def forward(self, contexts, target):  # 用单词ID表示contexts, target
        h = 0
        for i, layer in enumerate(self.in_layers):
            h += layer.forward(contexts[:, i])
        h *= 1 / len(self.in_layers)
        loss = self.ns_loss.forward(h, target)
        return loss
    
    # 反向传播
    def backward(self, dout=1):
        dout = self.ns_loss.backward(dout)
        dout *= 1 / len(self.in_layers)
        for layer in self.in_layers:
            layer.backward(dout)
        return None    
    

改进版的 CBOW 类的实现如下所示。（ch04/cbow.py）。

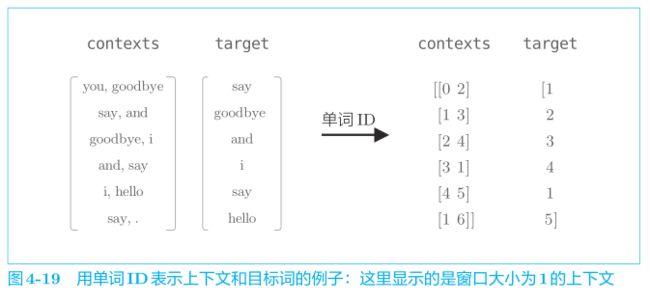
用单词ID表示contexts, target的例子：

可以看出，contexts 是一个二维数组，target 是一个一维数组，这样的数据被输入 forward(contexts, target) 中

  CBOW模型的学习代码

建立完层的初始化、正向传播、反向传播，接下来，我们来实现 CBOW 模型的学习部分，也就是训练部分。（ch04/train.py）

import sys
sys.path.append('..')
import numpy as np
from common import config
# 在用GPU运行时，请打开下面的注释（需要cupy）
# ===============================================
# config.GPU = True
# ===============================================
import pickle
from common.trainer import Trainer
from common.optimizer import Adam
from cbow import CBOW
from common.util import create_contexts_target, to_cpu, to_gpu
from dataset import ptb


# 设定超参数
window_size = 5 # 窗口大小为 5；一般而言，当窗口大小为 2~10、中间层的神经元个数（词向量的维数）为50～500时，结果会比较好。
hidden_size = 100
batch_size = 100
max_epoch = 10


# 读入数据，使用PTB 语料库比之前要大得多，因此学习需要很长时间（半天左右）。
corpus, word_to_id, id_to_word = ptb.load_data('train')
vocab_size = len(word_to_id)


contexts, target = create_contexts_target(corpus, window_size)
if config.GPU:
    contexts, target = to_gpu(contexts), to_gpu(target)
    
# 生成模型等
model = CBOW(vocab_size, hidden_size, window_size, corpus)
optimizer = Adam()
trainer = Trainer(model, optimizer)


# 开始学习
trainer.fit(contexts, target, max_epoch, batch_size)
trainer.plot()


# 保存必要数据，以便后续使用
word_vecs = model.word_vecs
if config.GPU:
    word_vecs = to_cpu(word_vecs)
params = {}
params['word_vecs'] = word_vecs.astype(np.float16)
params['word_to_id'] = word_to_id
params['id_to_word'] = id_to_word
pkl_file = 'cbow_params.pkl'  # 使用pickle功能进行文件保存
with open(pkl_file, 'wb') as f: 
    pickle.dump(params, f, -1)

ch04/cbow_params.pkl中提供了学习好的参数。如果不想等学习结束，可以使用本书提供的学习好的参数。根据学习环境的不同，学习到的权重数据也不一样。这是由权重初始化时用到的随机初始值、mini-bath 的随机选取，以及负采样的随机抽样造成的。因为这些随机性，最后得到的权重在各自的环境中会不一样。不过宏观来看，得到的结果（趋势）是类似的。

  CBOW模型的评价

现在，我们来评价一下上一节学习到的单词的分布式表示。使用 most_similar() 函数，该函数是用于显示和所给词最接近的单词（ch04/eval.py）。

import sys
sys.path.append('..')
from common.util import most_similar
import pickle


pkl_file = 'cbow_params.pkl'
with open(pkl_file, 'rb') as f:
    params = pickle.load(f)
    word_vecs = params['word_vecs']
    word_to_id = params['word_to_id']
    id_to_word = params['id_to_word']
    
querys = ['you', 'year', 'car', 'toyota']
for query in querys:
    most_similar(query, word_to_id, id_to_word, word_vecs, top=5) # 打印出最接近的5个词

运行上述代码，可以得到：

[query] you
 we: 0.610597074032
 someone: 0.591710150242
 i: 0.554366409779
 something: 0.490028560162
 anyone: 0.473472118378
    
[query] year
 month: 0.718261063099
 week: 0.652263045311
 spring: 0.62699586153
 summer: 0.625829637051
 decade: 0.603022158146
    
[query] car
 luxury: 0.497202396393
 arabia: 0.478033810854
 auto: 0.471043765545
 disk-drive: 0.450782179832
 travel: 0.40902107954
    
[query] toyota
 ford: 0.550541639328
 instrumentation: 0.510020911694
 mazda: 0.49361255765
 bethlehem: 0.474817842245
 nissan: 0.474622786045

我们看一下结果。在查询 you 的情况下，近似单词中出现了人称代词 i（= I）和 we 等。查询 year，可以看到 month、week 等表示时间区间的具有相同性质的单词。然后，查询 toyota，可以得到 ford、mazda 和 nissan 等表示汽车制造商的词汇。从这些结果可以看出，由CBOW 模型获得的单词的分布式表示具有良好的性质。

  CBOW模型的应用

关于 word2vec 的原理和实现，差不多都介绍完了。接下来我们看看它在实际应用中的例子。

在自然语言处理领域，单词的分布式表示之所以重要，原因就在于迁移学习（transfer learning）。迁移学习是指在某个领域学到的知识可以被应用于其他领域。

在解决自然语言处理任务时，一般不会使用 word2vec 从零开始学习词向量，而是先在大规模语料库（Wikipedia、Google News 等文本数据）上学习，然后将学习好的词向量应用于某个单独的任务。

比如，在文本分类、文本聚类、词性标注和情感分析等自然语言处理任务中，第一步的单词向量化工作就可以使用学习好的单词的分布式表示。在几乎所有类型的自然语言处理任务中，单词的分布式表示都有很好的效果！

将单词和文档转化为固定长度的向量是非常重要的。因为如果可以将自然语言转化为向量，就可以使用常规的机器学习方法（神经网络、SVM等），如图 4-21 所示。

在图 4-21 的流程中，单词的分布式表示的学习和机器学习系统的学习通常使用不同的数据集独立进行。

比如，单词的分布式表示使用Wikipedia 等通用语料库预先学习好，然后机器学习系统（SVM 等）再使用针对当前问题收集到的数据进行学习。但是，如果当前我们面对的问题存在大量的学习数据，则也可以考虑从零开始同时进行单词的分布式表示和机器学习系统的学习。

下面让我们结合具体的例子来说明一下单词的分布式表示的使用方法。

比如我们要开发一个可以对用户发来的邮件（吐槽等）自动进行分类的系统。根据邮件的内容将用户情感分为 3 类。如果可以正确地对用户情感进行分类，就可以按序浏览表达不满的用户邮件。如此一来，或许可以发现应用的致命问题，并尽早采取应对措施，从而提高用户的满意度。

要开发邮件自动分类系统，首先需要从收集数据（邮件）开始。

• 我们收集用户发送的邮件，并人工对邮件进行标注，打上表示3类情感的标签（positive/neutral/negative）。

• 标注工作结束后，用学习好的word2vec 将邮件转化为向量。

• 然后，将向量化的邮件及其情感标签输入某个情感分类系统（SVM 或神经网络等）进行学习。

如本例所示，可以基于单词的分布式表示将自然语言处理问题转化为向量，这样就可以利用常规的机器学习方法来解决问题。

  词向量的评价方法

使用 word2vec，我们得到了单词的分布式表示。那么，我们应该如何评价我们得到的分布式表示是好的呢？

此时，经常使用的评价指标有“相似度”和“类推问题”。

单词相似度的评价通常使用人工创建的“单词相似度评价集”来评估。用 0 ～ 10 的分数人工地对单词之间的相似度打分。然后，比较人给出的分数和 word2vec 给出的余弦相似度，考察它们之间的相关性。

类推问题的评价是指，诸如“king : queen = man : ?”这样的类推问题，根据正确率测量单词的分布式表示的优劣。比如，论文 [27] 中给出了一个类推问题的评价结果，其部分内容如图 4-23 所示。

在图 4-23 中，以 word2vec 的模型、单词的分布式表示的维数和语料库的大小为参数进行了比较实验，结果在右侧的 3 列中。

• Semantics列显示的是推断单词含义的类推问题（像“king : queen = actor : actress”这样询问单词含义的问题）的正确率

• Syntax 列是询问单词形态信息的问题，比如“bad : worst = good : best”。

由图 4-23 可知：

• 模型不同，精度不同（根据语料库选择最佳的模型）

• 语料库越大，结果越好（始终需要大数据）

• 单词向量的维数必须适中（太大会导致精度变差）

但是，单词的分布式表示的优劣评价指标取决于待处理问题的具体情况，比如应用的类型或语料库的内容等。也就是说，不能保证类推问题的评价高，目标应用的结果就一定好。

总结

本节我们基于简单CBOW模型出现的计算问题，进行了如下改进：

• 实现了 Embedding 层：保存单词的分布式表示，在正向传播时，提取单词 ID对应的向量

• 引入负采样：负采样通过仅关注部分单词实现计算的高速化。

能够实现加速的根本原因：

• 利用“部分”数据而不是“全部”数据

• 使用近似计算来加速（比如负采样，只抽取部分负例）

word2vec 的迁移学习能力非常重要，它的单词的分布式表示可以应用于各种各样的自然语言处理任务，基本上是所有NLP任务的基础。

参考文献

[27]  Pennington, Jeffrey, Richard Socher, Christopher D. Manning.Glove:  Global Vectors for Word Representation[J]. EMNLP. Vol.14. 2014.

说个正事哈

由于微信平台算法改版，公号内容将不再以时间排序展示，如果大家想第一时间看到我们的推送，强烈建议星标我们和给我们多点点【在看】。星标具体步骤为：

（1）点击页面最上方“深度学习自然语言处理”，进入公众号主页。

（2）点击右上角的小点点，在弹出页面点击“设为星标”，就可以啦。

感谢支持，比心。

投稿或交流学习，备注：昵称-学校（公司）-方向，进入DL&NLP交流群。

方向有很多：机器学习、深度学习，python，情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。

记得备注呦

推荐两个专辑给大家：

专辑 | 李宏毅人类语言处理2020笔记

专辑 | NLP论文解读

专辑 | 情感分析

整理不易，还望给个在看！