pytorch之交叉熵（笔记四）

 师傅说过一句话：线性回归用二次代价函数，分类使用交叉熵。

通过一个例子观察一下：

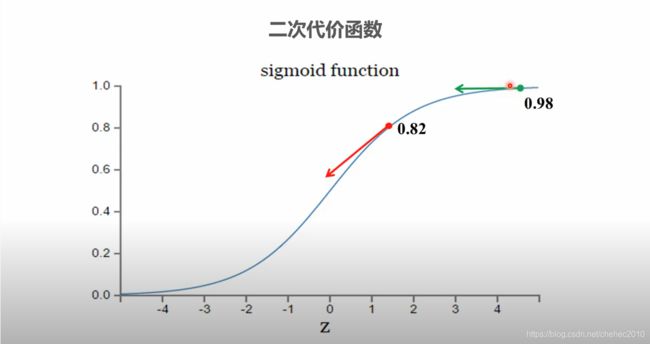
通过观察发现，输入是0.82的比输入是0.98的收敛的更快，为什么呢？为我们通过sigmod函数观察一下。

原因是在0.98的时候收敛的比较平缓，因为斜率比较小，0.82的时候斜率大，收敛的就比较快。

 交叉熵的概念

交叉熵和二次代价函数对比。

二次代价函数：代码请参考（我的博客pytorch之mnist手写数字识别（笔记三））：https://mp.csdn.net/editor/html/116517592

测试结果：

F:\开发工具\pythonProject\tools\venv\Scripts\python.exe F:/开发工具/pythonProject/tools/pytools/pytools03.py
torch.Size([64, 1, 28, 28])
torch.Size([64])
epoch: 0
Test acc:0.8886
epoch: 1
Test acc:0.903
epoch: 2
Test acc:0.9075
epoch: 3
Test acc:0.91
epoch: 4
Test acc:0.9142
epoch: 5
Test acc:0.9157
epoch: 6
Test acc:0.9174
epoch: 7
Test acc:0.9171
epoch: 8
Test acc:0.9188
epoch: 9
Test acc:0.9189

Process finished with exit code 0

交叉熵（mnist手写数字举例）：

import numpy as np
import torch
from torch import nn,optim
from torch.autograd import Variable
from torchvision import datasets,transforms
from torch.utils.data import DataLoader
#训练集
train_dataset=datasets.MNIST(root='./', #存放到项目目录下
                             train=True,  #是训练数据
                             transform=transforms.ToTensor(),  #转换成基本类型tensor数据
                             download=True) #需要下载
#测试集
test_dataset=datasets.MNIST(root='./',
                             train=False,
                             transform=transforms.ToTensor(),
                             download=True)

#每次训练图片的数量
batch_size=64
#装在训练集数据
train_loader=DataLoader(dataset=train_dataset,
                        batch_size=batch_size,
                        shuffle=True
                        )
#加载训练集
test_loader=DataLoader(dataset=test_dataset,
                       batch_size=batch_size,
                       shuffle=True
                       )
for i,data in enumerate(train_loader):
    inputs,labels=data
    print(inputs.shape)
    print(labels.shape)
    break

#定义网络结构
class Net(nn.Module):
    def __init__(self):
        super(Net,self).__init__()#调用父类方法
        self.fc1=nn.Linear(784,10)#28*28=784,10个输出
        self.softmax=nn.Softmax(dim=1)#对第一个维度计算他的概率值
    def forward(self,x):
        #[64,1,28,28]----(64,784)四维数据编程2维数据
        x=x.view(x.size()[0],-1)#-1表示自动匹配
        x=self.fc1(x)#传递给全连接层
        x=self.softmax(x)#传递给激活函数
        return x

LR=0.5
#定义模型
model=Net()
#定义代价函数(交叉熵)
mse_loss=nn.CrossEntropyLoss()
#定义优化器
optimizer=optim.SGD(model.parameters(),LR)

def train():
    for i,data in enumerate(train_loader):
        #获得一个皮次数据和标签
        inputs,labels=data
        #获得模型预测结果（64,10）
        out=model(inputs)
        #交叉熵代价函数out（batch,C）labels(batch)
        loss=mse_loss(out,labels)
        #梯度清零
        optimizer.zero_grad()
        #计算梯度
        loss.backward()
        #修改权值
        optimizer.step()

#测试
def test():
    correct=0
    for i,data in enumerate(test_loader):
        #获取一个批次的数据和标签
        inputs,labels=data
        #获得模型的预测结果（64,10）
        out=model(inputs)
        #获取最大值，以及最大值所在的位置
        _,predicted=torch.max(out,1)
        # 预测正确的数量
        correct += (predicted == labels).sum()
    print("Test acc:{0}".format(correct.item()/len(test_dataset)))

for epoch in range(10):
    print("epoch:",epoch)
    train()
    test()

测试结果：

F:\开发工具\pythonProject\tools\venv\Scripts\python.exe F:/开发工具/pythonProject/tools/pytools/pytools031.py
torch.Size([64, 1, 28, 28])
torch.Size([64])
epoch: 0
Test acc:0.9035
epoch: 1
Test acc:0.9119
epoch: 2
Test acc:0.9183
epoch: 3
Test acc:0.9189
epoch: 4
Test acc:0.921
epoch: 5
Test acc:0.9202
epoch: 6
Test acc:0.9231
epoch: 7
Test acc:0.9233
epoch: 8
Test acc:0.9243
epoch: 9
Test acc:0.9251

Process finished with exit code 0

测试结果对比，同样训练次数，交叉熵的收敛速度更快，预测结果准确度更高。