粒子群优化算法python_粒子群优化算法(PSO)
最近有人咨询了PSO优化模糊控制论域的问题,正好简单介绍一下粒子群算法。
1、粒子群算法
粒子群算法是一种智能优化算法。关于智能,个人理解,不过是在枚举法的基础上加上了一定的寻优机制。试想一下枚举法,假设问题的解空间很小,比如一个函数 y = x^2 ,解空间在[-1,1],现在求这个函数的最小值,我们完全可以使用枚举法,比如在这里,在解空间[-1,1]上,取1000等分,也就是步长为0.002,生成1000个x值,然后代入函数中,找到这1000个最小的y就可以了。然而实际情况不是这样的,比如为什么选1000等分,不是1w,10w等分,很显然等分的越大,计算量也就越大,带来的解当然也就越精确,那么实际问题中如何去平衡这两点呢?也就是既要计算量小(速度快),也要准确(精度高),这就是智能算法的来源了,一般的智能算法基本上都是这样的,在很大的搜索空间上,即保证了速度快,也能比较好的找到最优解。
再来看看粒子群算法(也称PSO算法),也是一种进化算法,模拟生物群体的觅食行为,是一种群体智能算法,类似的算法想遗传算法,模拟退火算法等等。PSO是通过当前已知种群寻找到的所有解来决定新的解的寻找方向,也就是新解的生成方式依赖于这些种群历史上寻找的所有解。
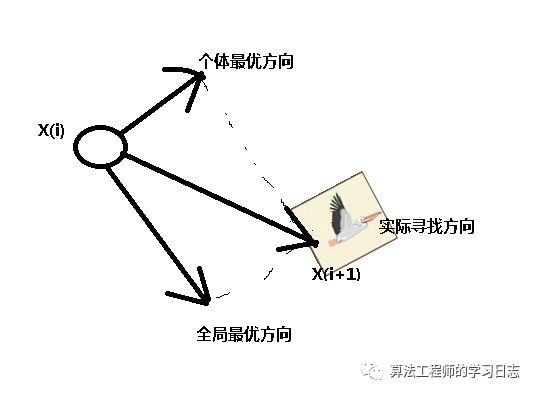
形象的理解比如下图:
开始随机生成一堆种群,那么这些种群之间的每个个体可以相互交流,比如下一时刻,A告诉B说我的解比你好,那么B就往A那个地方飞,也就是B的解朝着A的解方向变化,当然所有粒子间都这样操作,想想一旦粒子群中间有一个粒子找到了一个最优解,是不是所有的粒子会一窝蜂朝着这个方向而去了,而在这个去的过程中,万一某个粒子找到了一个更好的解,那它还会走吗?不会了,它就告诉剩下的所有粒子说我的解更好呀,大家快来呀(很无私的),然后所有粒子又一窝蜂的照着这个粒子方向前进,当然在这个前进的过程中可能又会产生新的解,就这样一步步的迭代,最终慢慢的趋近于一个最优解,这个解是不是全局最优解,不知道,可能是,也可能不是,取决于原始问题的复杂程度,也取决于粒子前进的多少等等。
粒子群算法相对于其他算法来说还是有很多优点的,典型的就是计算速度很快,在每次迭代时,所有粒子同时迭代,是一种并行计算方式,而且粒子的更新方式简单,朝着一个优秀解方向更新。这个优秀解包括两个部分:
1)一个是朝着自己在迭代的历史上找到的个体最优解gbest前进
2)一个是朝着群体在得带历史上找到的全体最优解zbest前进
现在还有一个问题就是每次迭代的时候更新多少呢?也就是自变量的增加步长了,我们用一个速度量V来表示,也就是每个粒子的更新速度了,公式化的表示就是这样的:
Vid(t+1)=Vidt+c1∗rand∗(Pid−xid(t))+c2∗rand∗(Pgd−xid(t))" role="presentation" style=" box-sizing: border-box; outline: 0px; display: inline; line-height: normal; word-spacing: normal; word-wrap: break-word; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border-width: 0px; border-style: initial; border-color: initial; ">Vid(t+1)=Vidt+c1∗rand∗(Pid−xid(t))+c2∗rand∗(Pgd−xid(t))Vid(t+1)=Vidt+c1∗rand∗(Pid−xid(t))+c2∗rand∗(Pgd−xid(t))
其中自变量的更新为: xi(t+1)=xi(t)+Vi(t)" role="presentation" style=" box-sizing: border-box; outline: 0px; display: inline; line-height: normal; font-size: 16px; text-align: left; word-wrap: break-word; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border-width: 0px; border-style: initial; border-color: initial; color: rgba(0, 0, 0, 0.75); font-family: -apple-system, "SF UI Text", Arial, "PingFang SC", "Hiragino Sans GB", "Microsoft YaHei", "WenQuanYi Micro Hei", sans-serif; font-variant-ligatures: common-ligatures; background-color: rgb(255, 255, 255); ">xi(t+1)=xi(t)+Vi(t)xi(t+1)=xi(t)+Vi(t) 从上面的速度V的更新而已看到,c1那项就是朝着自己的最优解前进,c2那一项就是朝着全局最优解那前进。用简单的图表示如下:
2、粒子群的算法步骤
粒子群的核心部分就是上面说到的那两个公式,一个是速度的更新方式,另一个是位置的更新方式,重点还是速度的更新方式;
总结来说,粒子群的算法步骤如下:
初始化粒子群个体;
计算每个个体的适应度值(函数值)作为评判好坏的标准;
找到每个个体自己在所有迭代过程中的最优解Pbest;
找到所有个体在所有迭代过程中的最优解Zbest;
根据速度公式更新速度;
根据位置公式更新位置;
重复步骤二直至迭代次数结束
这里有几个参数需要说一下,
关于速度V,限制速度的范围,比如需要设置一个最大速度,防止更新过快;
关于c1与c2,这两个参数代表学习因子,决定跟随历史优秀解的能力;
关于粒子数与迭代次数,粒子数一般50-100,迭代次数视问题而定了;
3、Matlab实现
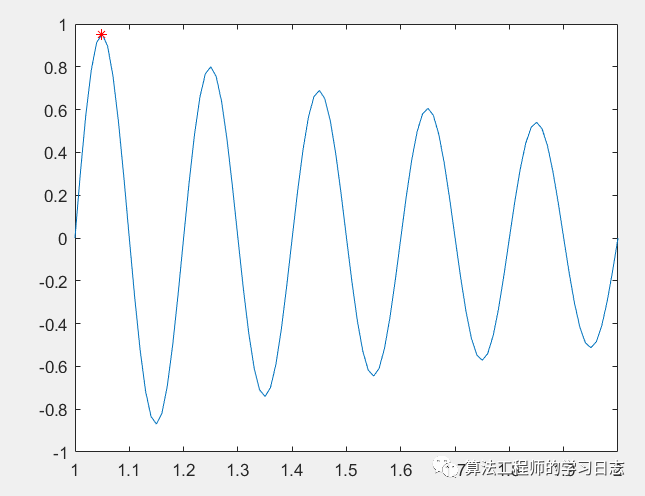
%% I. 清空环境clcclearclose all%% II. 绘制目标函数曲线图x = 1:0.01:2;fun = @(x)sin(10 * pi * x) ./ x;y = fun(x);figureplot(x, y)hold on%% III. 参数初始化c1 = 1.49445;c2 = 1.49445; maxgen = 50; % 进化次数 sizepop = 10; %种群规模 Vmax = 0.5; %速度的范围,超过则用边界值。Vmin = -0.5; popmax = 2; %个体的变化范围popmin = 1; %% IV. 产生初始粒子和速度for i = 1:sizepop % 随机产生一个种群 pop(i,:) = (rands(1) + 1) / 2 + 1; %初始种群,rands产生(-1,1),调整到(1,2) V(i,:) = 0.5 * rands(1); %初始化速度 % 计算适应度 fitness(i) = fun(pop(i,:)); end %% V. 个体极值和群体极值[bestfitness,bestindex] = max(fitness);zbest = pop(bestindex,:); %全局最佳gbest = pop; %个体最佳fitnessgbest = fitness; %个体最佳适应度值fitnesszbest = bestfitness; %全局最佳适应度值 %% VI. 迭代寻优for i = 1:maxgen for j = 1:sizepop % 速度更新 V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:)); V(j,V(j,:)>Vmax) = Vmax; V(j,V(j,:) % 种群更新 pop(j,:) = pop(j,:) + V(j,:); pop(j,pop(j,:)>popmax) = popmax; pop(j,pop(j,:) % 适应度值更新 fitness(j) = fun(pop(j,:)); end for j = 1:sizepop % 个体最优更新 if fitness(j) > fitnessgbest(j) gbest(j,:) = pop(j,:); fitnessgbest(j) = fitness(j); end % 群体最优更新 if fitness(j) > fitnesszbest zbest = pop(j,:); fitnesszbest = fitness(j); end end yy(i) = fitnesszbest; end %% VII. 输出结果并绘图disp([fitnesszbest zbest])plot(zbest, fitnesszbest,'r*')figureplot(yy)title('最优个体适应度','fontsize',12);xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);结果如下
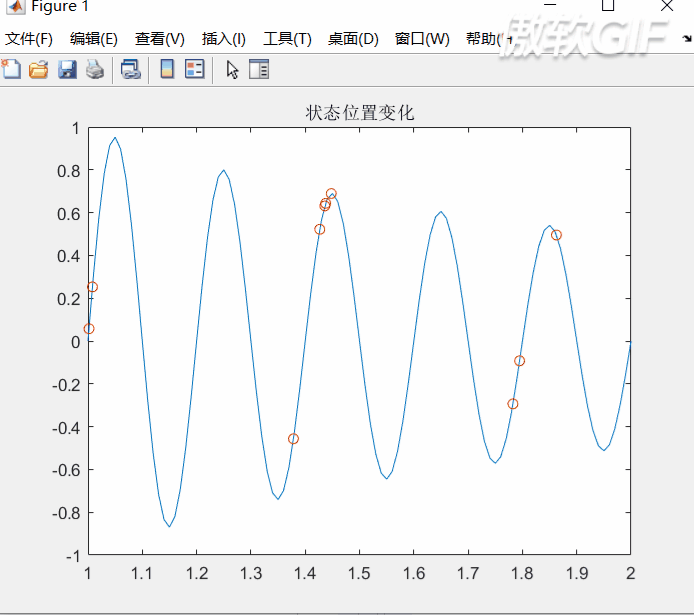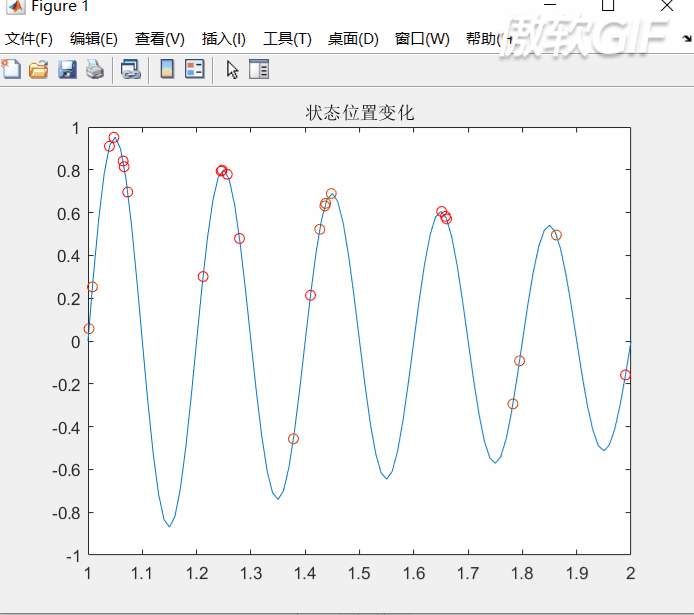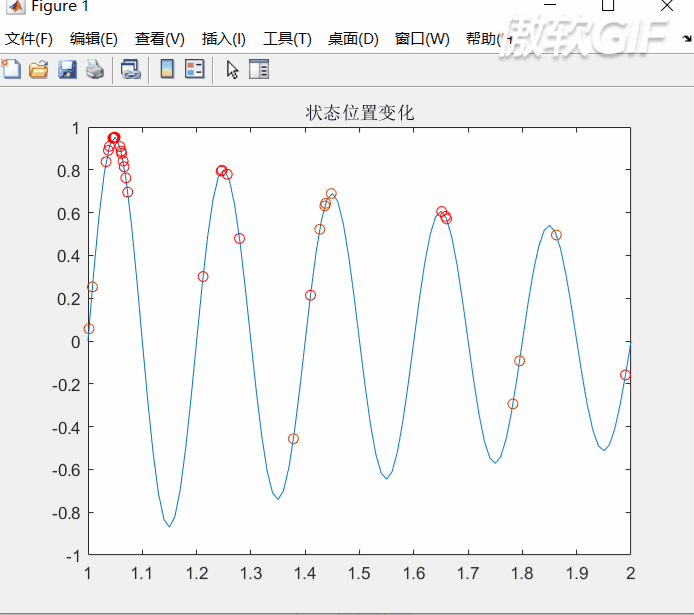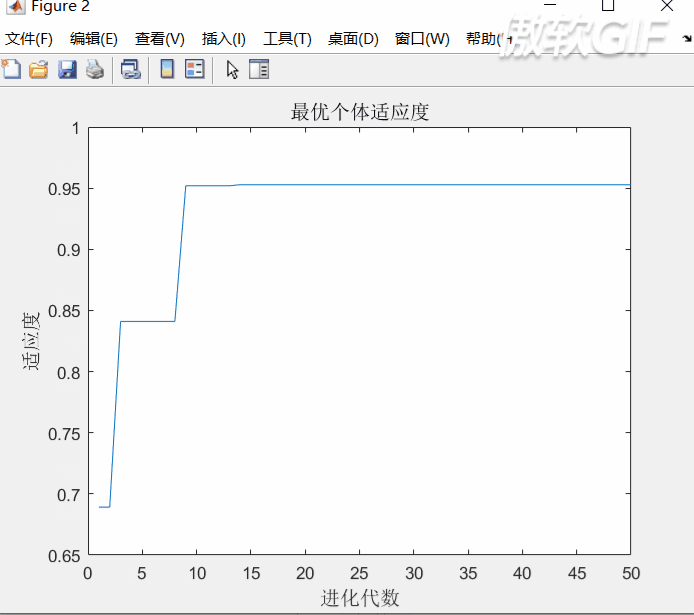
动画过程