基于优选策略的自适应蚁狮优化算法
文章目录
- 一、理论基础
-
- 1、蚁狮优化算法
- 2、优选策略的自适应蚁狮优化算法
-
- (1)自适应边界
- (2)优选轮盘赌策略
- (3)动态比例系数
- 二、算法步骤
- 三、仿真实验与结果分析
- 四、参考文献
- 五、Matlab仿真程序
一、理论基础
1、蚁狮优化算法
请参考这里。
2、优选策略的自适应蚁狮优化算法
(1)自适应边界
提出自适应边界策略,改进增加蚂蚁在围绕蚁狮游走时的多样性: I = 1 0 w t T ( 0.5 + s i n ( t π 2 T ⋅ r a n d ) ) (1) I=10^w\frac tT\left(0.5+sin\left(\frac{t\pi}{2T}\cdot rand\right)\right)\tag{1} I=10wTt(0.5+sin(2Ttπ⋅rand))(1)其中, r a n d rand rand为 [ 0 , 1 ] [0,1] [0,1]之间的随机数。 t > { 0.1 T , w = 2 0.5 T , w = 3 0.75 T , w = 4 0.9 T , w = 5 0.95 T , w = 6 (2) t>\begin{dcases}0.1T,\quad\,\,\, w=2\\0.5T,\quad\,\,\, w=3\\0.75T,\quad w=4\\0.9T,\quad\,\,\, w=5\\0.95T,\quad w=6\end{dcases}\tag{2} t>⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧0.1T,w=20.5T,w=30.75T,w=40.9T,w=50.95T,w=6(2)随着进化代数增加, 1 0 w 10^w 10w呈线性分段指数递增, t T \frac tT Tt线性递增, ( 0.5 + s i n ( t π 2 T ⋅ r a n d ) ) \left(0.5+sin\left(\frac{t\pi}{2T}\cdot rand\right)\right) (0.5+sin(2Ttπ⋅rand))在 ( 0.5 , 1.5 ) (0.5,1.5) (0.5,1.5)内呈随机非线性递增趋势。整体而言, I I I值随进化代数增加呈现具有一定随机性的非线性自适应递增趋势,于是边界大小随进化代数呈现具有一定随机性的非线性自适应递减趋势,从而提高蚂蚁围绕蚁狮游走的随机性和多样性,提高算法的开发能力和全局搜索能力,有利于找到全局最优解。
(2)优选轮盘赌策略
本文对轮盘赌选择进行改进,将初始算法中用于轮盘赌选择的蚁狮根据适应度大小进行排序,然后设定:如果 A < A ⋅ P ⋅ r a n d A
(3)动态比例系数
改进 R A t R_A^t RAt和 R E t R_E^t REt的比例系数,让不同时期两种游走方式占有的权重不同。算法前期以围绕轮盘赌选择的蚁狮游走方式为主,后期以围绕精英蚁狮的游走方式为主。改进后的动态比例系数为 A n t i t = ( 0.8 − 0.8 t T ⋅ r a n d ) R A t + R E t ( 0.2 + 0.8 t T ⋅ r a n d ) (3) Ant^t_i=(0.8-0.8\frac tT\cdot rand)R_A^t+R_E^t(0.2+0.8\frac tT\cdot rand)\tag{3} Antit=(0.8−0.8Tt⋅rand)RAt+REt(0.2+0.8Tt⋅rand)(3)其中, R A t R_A^t RAt为蚂蚁在第 t t t次迭代时围绕轮盘赌所选蚁狮进行随机游走后的位置, R E t R_E^t REt为蚂蚁在第 t t t次迭代时围绕精英蚁狮进行随机游走后的位置, t t t为当前迭代次数, T T T为最大迭代次数, r a n d rand rand为 ( 0 , 1 ) (0,1) (0,1)间均匀分布的随机数。
通过式(3)的改进,算法初期主要围绕轮盘赌选择蚁狮游走,同时也逐渐增强最优蚁狮的方向性影响。后期主要围绕精英蚁狮游走,兼有一定的随机性,有效提高算法前期的探索能力和后期的开发能力。同时动态比例系数的使用也在一定程度上提升蚂蚁种群的多样性。
二、算法步骤
三、仿真实验与结果分析
将改进蚁狮算法(PSALO)与原始蚁狮算法(ALO)、樽海鞘群算法(SSA)进行对比,仿真30次,每次迭代500次,种群规模为30。以F1~F3为例。
下图是F1的对比曲线。
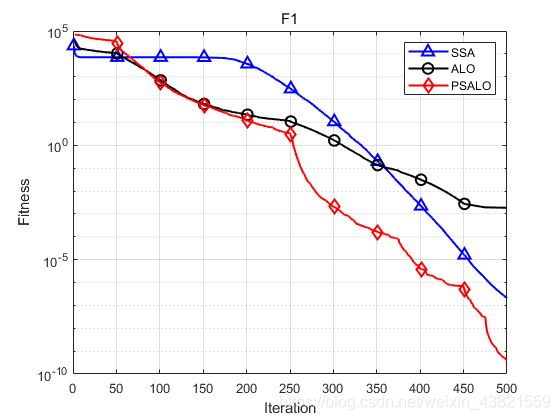 三种算法的最大值、最小值、平均值和标准差显示如下:
三种算法的最大值、最小值、平均值和标准差显示如下:
函数:F1
SSA:最大值: 1.976e-06,最小值:3.3803e-08,平均值2.093e-07,标准差:3.9333e-07
ALO:最大值: 0.0097103,最小值:0.00022597,平均值0.0018599,标准差:0.0022659
PSALO:最大值: 1.1972e-09,最小值:1.7294e-11,平均值3.9346e-10,标准差:3.428e-10
下图是F2的对比曲线。
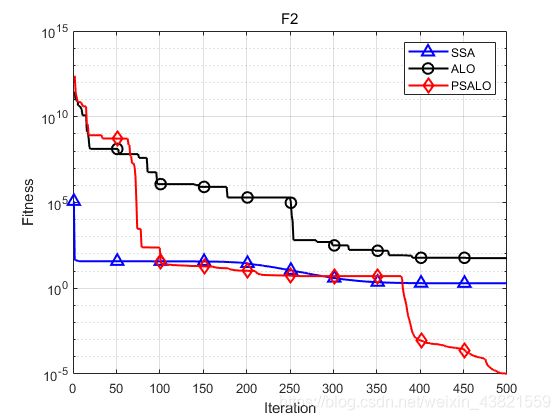 三种算法的最大值、最小值、平均值和标准差显示如下:
三种算法的最大值、最小值、平均值和标准差显示如下:
函数:F2
SSA:最大值: 5.0543,最小值:0.12765,平均值1.9419,标准差:1.4266
ALO:最大值: 127.5844,最小值:5.1073,平均值56.8097,标准差:48.045
PSALO:最大值: 2.1726e-05,最小值:4.3211e-06,平均值1.0354e-05,标准差:5.0614e-06
下图是F3的对比曲线。
 三种算法的最大值、最小值、平均值和标准差显示如下:
三种算法的最大值、最小值、平均值和标准差显示如下:
函数:F3
SSA:最大值: 3008.01,最小值:236.0645,平均值1270.2519,标准差:616.1047
ALO:最大值: 13305.4836,最小值:1777.0977,平均值4707.7349,标准差:2533.4001
PSALO:最大值: 3.2929e-08,最小值:2.662e-09,平均值1.3591e-08,标准差:8.0512e-09
综上,PSALO具有较好的进化寻优性能,求解精度、收敛速度和稳定性均较优。
四、参考文献
[1] 刘景森, 霍宇, 李煜. 优选策略的自适应蚁狮优化算法[J]. 模式识别与人工智能, 2020(2).
五、Matlab仿真程序
下载地址:
https://download.csdn.net/download/weixin_43821559/18521267
