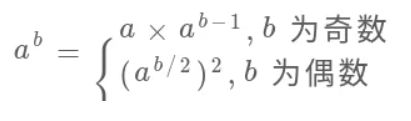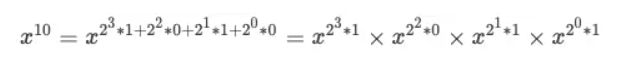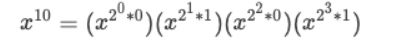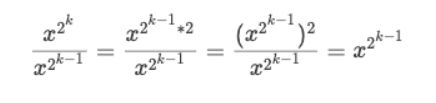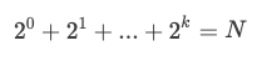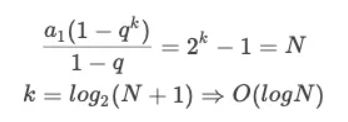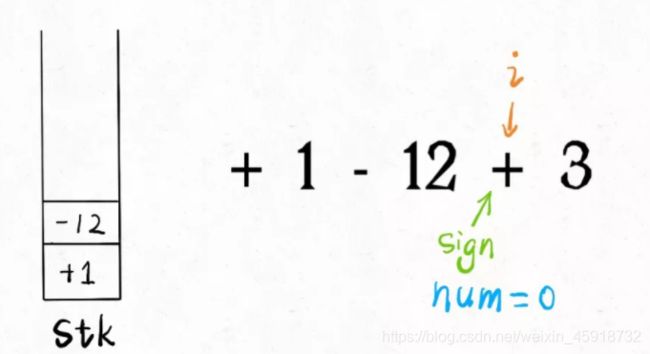【数学运算技巧&刷题熟练】高频面试题系列&结合书籍记录一些数学小技巧
素数寻找/快速开方、 模幂运算、 位运算……
c++ 二进制运算?一一下 四种理解。
一、数学技巧——二分、连乘模、快速幂运算技巧
1.0 快速开方
x的平方根——使用二分查找算法
// 通过二分查找,找到方大于x 直至刚好小于x的下确界
int mySqrt2(int x)
{
// if (x == 0)
// return x;
// int l = 1, r = x, mid, sqrt;
// while (l <= r)
// {
// mid = l + (r - l) / 2;
// sqrt = x / mid;
// if (sqrt == mid)
// {
// return mid;
// }
// else if (mid > sqrt)
// {
// r = mid - 1;
// }
// else
// {
// l = mid + 1;
// }
// }
// return r;
if (x == 0)
return 0;
int left = 1; //gai
int right = x; // 左闭右闭
// 查找所以等于
while (left <= right)
{
// int mid = (left + right) / 2; // 会溢出!所以最好用下面一行的!
int mid = left + (right - left) / 2;
int sqr2 = x / mid; // 重点
if (sqr2 == mid)
{
return mid;
}
else if (sqr2 < mid)
{
right = mid - 1;
}
else if (sqr2 > mid)
{
left = mid + 1;
}
}
return right; // 返回一个 刚好的下确界 【重点!】
}
// 牛顿迭代法求解方程.
int mySqrt3(int a)
{
long x = a;
while (x * x > a)
{
x = (x + a / x) / 2;
}
return x;
}
1.1 技巧
一些技巧,防止直接
+或者*溢出数据。
- 二分法数学方法
比如在二分查找中,我们求中点索引时用(l+r)/2转化成l+(r-l)/2,避免溢出的同时得到正确的结果。 - 模运算 中比较常见的运算技巧:
(a*b)%k = (a%k)(b%k)%k
证明很简单,假设:
a=Ak+B;b=Ck+D
其中 A,B,C,D 是任意常数,那么:
ab = ACk^2+ADk+BCk+BD
ab%k = BD%k
又因为:
a%k = B;b%k = D
所以:
(a%k)(b%k)%k = BD%k
综上,就可以得到我们化简求模的等式了。
换句话说,对乘法的结果求模,等价于先对每个因子都求模,然后对因子相乘的结果再求模。
那么就可以修改之前的mypow函数,翻译这个递归公式,再加上求模的运算:
int base = 1337;
int mypow(int a, int k) {
if (k == 0) return 1;
a %= base;
if (k % 2 == 1) {
// k 是奇数
return (a * mypow(a, k - 1)) % base;
} else {
// k 是偶数
int sub = mypow(a, k / 2);
return (sub * sub) % base;
}
}
这个递归解法很好理解对吧,如果改写成迭代写法,那就是大名鼎鼎的快速幂算法。至于如何改成迭代,很巧妙,这里推荐一位大佬的文章 客户端基本不用的算法系列:快速幂。
虽然对于题目,这个优化没有啥特别明显的效率提升,但是这个求幂算法已经升级了,以后如果别人让你写幂算法,起码要写出这个算法。
1.2 超级次方题目

这个算法其实就是广泛应用于离散数学的模幂算法,至于为什么要对 1337 求模我们不管,单就这道题可以有三个难点:
一是如何处理用数组表示的指数,现在b是一个数组,也就是说b可以非常大,没办法直接转成整型,否则可能溢出。你怎么把这个数组作为指数,进行运算呢?
**二是如何得到求模之后的结果?**按道理,起码应该先把幂运算结果算出来,然后做% 1337这个运算。但问题是,指数运算你懂得,真实结果肯定会大得吓人,也就是说,算出来真实结果也没办法表示,早都溢出报错了。
三是如何高效进行幂运算,进行幂运算也是有算法技巧的,如果你不了解这个算法,后文会讲解。
那么对于这几个问题,我们分开思考,逐个击破。
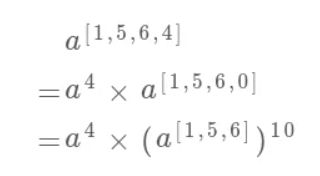
看到这,我们的老读者肯定已经敏感地意识到了,这就是递归的标志呀!因为问题的规模缩小了:
superPow(a, [1,5,6,4])
=> superPow(a, [1,5,6])
那么,发现了这个规律,我们可以先简单翻译出代码框架:
// 计算 a 的 k 次方的结果
// 后文我们会手动实现
int mypow(int a, int k);
int superPow(int a, vector<int>& b) {
// 递归的 base case
if (b.empty()) return 1;
// 取出最后一个数
int last = b.back();
b.pop_back();
// 将原问题化简,缩小规模递归求解
int part1 = mypow(a, last);
int part2 = mypow(superPow(a, b), 10);
// 合并出结果
return part1 * part2;
}
到这里,应该都不难理解吧!我们已经解决了b是一个数组的问题,现在来看看如何处理 mod,避免结果太大而导致的整型溢出。
加之 前一节的:模公式 + 快速幂;我们可以写出新的 mypow()
int base = 1337;
int mypow(int a, int k) {
if (k == 0) return 1;
a %= base;
if (k % 2 == 1) {
// k 是奇数
return (a * mypow(a, k - 1)) % base;
} else {
// k 是偶数
int sub = mypow(a, k / 2);
return (sub * sub) % base;
}
}
int superPow(int a, vector<int>& b) {
if (b.empty()) return 1;
int last = b.back();
b.pop_back();
int part1 = mypow(a, last);
int part2 = mypow(superPow(a, b), 10);
// 每次乘法都要求模
return (part1 * part2) % base;
}
我的题解:C++
class Solution {
public:
/**
* @Description: 方法一:【未加超级幂】 模运算——拆解为递归 +有公式; 幂运算——使用快速幂 运算的公式。
* @param {int} a
* @return {*}
* @notes:
*/
int base = 1337;
int mypow(int a, int k){
a %= base;
int res = 1;
for(int i = 0; i < k ; i++){
res *= a;
res %= base;
}
return res;
}
int superPow(int a, vector<int>& b) {
if(b.empty()) return 1;
int k = b.back();
b.pop_back();
// 开始递归
int left = mypow(a, k);
int right = mypow(superPow(a, b), 10);
return (left * right) % 1337;
}
/**
* @Description: 方法二:【加之 超级幂】 模运算——拆解为递归 +有公式; 幂运算——使用快速幂 运算的公式。
* @param {int} a
* @return {*}
* @notes:
*/
int base = 1337;
// 修改mypow
int mypow(int a, int k){
// 注意递归时——必须要有 base结束的边界!
if(k == 0) return 1;
a %= base; // 这个必须加上!因为不加就会溢出!
if(k%2 != 0){
// k是奇数
return (a * mypow(a, k-1))%base;
}else{
// k 是偶数
int temp = mypow(a, k/2);
return temp*temp % base;
}
}
int superPow(int a, vector<int>& b) {
if(b.empty()) return 1;
int k = b.back();
b.pop_back();
// 开始递归
int left = mypow(a, k);
int right = mypow(superPow(a, b), 10);
return (left * right) % 1337;
}
};
1.3 快速幂
关键记忆 最后形成的
qpow()函数。
幂运算是我们平时写代码的时候最常用的运算之一。根据幂运算的定义我们可以知道,如果我们要求 x 的 N 次幂,那么想当然的就会写出一个 N 次的循环,然后累乘得到结果。所以我们要求幂运算的复杂度仍旧是 O(N)?
那么有没有一种更快的方法呢?
这里给出一种在计算机领域常用的快速幂算法,将 O(N) 降为 O(logN)。
我通过例子来讲解这个优化过程:
假设我们要算 x 的 n 次幂,使用累乘来编写代码:
1res = 1
2for i in range(n):
3 res *= x
好的,我们已经完成了 O(N) 的解法。
1.3.1 二进制拆分
为了优化这个算法,我们接下来进行数学推导:
我们继续思考当 N = 10 这个具体场景,我们可以把 10 写成二进制来表示 1010(BIN),然后我们模拟一次二进制转十进制的过程(复习一下大学知识):
我用下划线把二进制的 1010 标识出来,这样大家就可以发现二进制和十进制转换时的代数式规律。
继续回想刚才的场景,那么我们求 x 的 10 次幂,则式子我们可以写成这样:
我们按照二进制低位到高位从左往右交换一下位置:
我们关注相邻的两项,如果我们不考虑幂指数的 *0 和 *1 ,我们只看前半部分,会发现有这么一个规律:
也就是说,不考虑幂指数的 *0 和 *1 右式,左式每次只要每次乘以自身,就是下一项的左式。在我们的例子中其实就是:
用编程思维来考虑这个问题,只要我们从 x 开始维护这么一个左式,每一次迭代都执行 x *= x,然后每次遇到右边是 *1 的情况,就记录一下 res *= x 是不是就能模拟咱们二进制拆分的计算思路了呢?
1.3.2 编程实现一下 x 的 10 次方
我们用上面的思路,通过代码来计算一下 2 的 10 次方,答案应该是 1024。
1#include <iostream>
2using namespace std;
3
4int main() {
5 int n = 10; // 幂指数,下面通过二进制拆分成 1010
6 int x = 2; // 底数
7 int res = 1; // 累乘的答案
8 while (n) {
9 // 去除二进制的最低位,也就是上面推导中的右式,如果 n & 1 == 1,说明是 *1
10 if (n & 1) {
11 // 如果是 *1,则根据我们观察出来的规律,对维护的结果做累乘
12 res *= x;
13 }
14 // 转换到下一位
15 x *= x;
16 // 二进制右移一位,目的是取到下一个低位二进制
17 n >>= 1;
18 }
19 cout << res << endl; // 1024
20 return 0;
21}
是不是发现非常的简单!我们至此已经实现了快速幂算法。我们将 n, x 做成参数,编写一个快速幂的方法:
1#include <iostream>
2using namespace std;
3
4int qpow(int x, int n) {
5 int res = 1;
6 while (n) {
7 if (n & 1) res *= x;
8 x *= x;
9 n >>= 1;
10 }
11 return res;
12}
13
14int main() {
15 cout << qpow(2, 10) << endl; // 1024
16 cout << qpow(4, 2) << endl; // 16
17 cout << qpow(5, 3) << endl; // 125
18 cout << qpow(10, 6) << endl; // 1000000
19 return 0;
20}
1.3.3 复杂度
通过上面对幂指数的拆分,发现快速幂只需要循环拆分的项数就可以完成整个幂运算。
我们不妨设求 x 的 N 次方,并且令 x 的所有二进制位都为 1,就可以得到下面这个等式:
那么其实,k 就是计算机需要计算的次数,也就是时间复杂度。套入公比是 1 的等比数列前 k 项和来反推 k 的大小:
二、经典面试题:最长回文子串
回文串是面试常常遇到的问题(虽然问题本身没啥意义),本文就告诉你回文串问题的核心思想是什么。
首先,明确一下什:回文串就是正着读和反着读都一样的字符串。
比如说字符串aba和abba都是回文串,因为它们对称,反过来还是和本身一样。反之,字符串abac就不是回文串。
可以看到回文串的的长度可能是奇数,也可能是偶数,这就添加了回文串问题的难度,解决该类问题的核心是双指针。下面就通过一道最长回文子串的问题来具体理解一下回文串问题:
图片
string longestPalindrome(string s) {
}
一、思考
对于这个问题,我们首先应该思考的是,给一个字符串s,如何在s中找到一个回文子串?
有一个很有趣的思路:既然回文串是一个正着反着读都一样的字符串,那么如果我们把s反转,称为s’,然后在s和s’中寻找最长公共子串,这样应该就能找到最长回文子串。
比如说字符串abacd,反过来是dcaba,它俩的最长公共子串是aba,也就是最长回文子串。
但是这个思路是错误的,比如说字符串aacxycaa,反转之后是aacyxcaa,最长公共子串是aac,但是最长回文子串应该是aa。
虽然这个思路不正确,但是这种把问题转化为其他形式的思考方式是非常值得提倡的。
下面,就来说一下正确的思路,如何使用双指针。
寻找回文串的问题核心思想是:从中间开始向两边扩散来判断回文串。对于最长回文子串,就是这个意思:
for 0 <= i < len(s):
找到以 s[i] 为中心的回文串
更新答案
但是呢,我们刚才也说了,回文串的长度可能是奇数也可能是偶数,如果是abba这种情况,没有一个中心字符,上面的算法就没辙了。所以我们可以修改一下:
for 0 <= i < len(s):
找到以 s[i] 为中心的回文串
找到以 s[i] 和 s[i+1] 为中心的回文串
更新答案
PS:读者可能发现这里的索引会越界,等会会处理。
二、代码实现
按照上面的思路,先要实现一个函数来寻找最长回文串,这个函数是有点技巧的:
图片
为什么要传入两个指针l和r呢?因为这样实现可以同时处理回文串长度为奇数和偶数的情况:
for 0 <= i < len(s):
# 找到以 s[i] 为中心的回文串
palindrome(s, i, i)
# 找到以 s[i] 和 s[i+1] 为中心的回文串
palindrome(s, i, i + 1)
更新答案
下面看下longestPalindrome的完整代码:
图片
至此,这道最长回文子串的问题就解决了,时间复杂度 O(N^2),空间复杂度 O(1)。
值得一提的是,这个问题可以用动态规划方法解决,时间复杂度一样,但是空间复杂度至少要 O(N^2) 来存储 DP table。这道题是少有的动态规划非最优解法的问题。
另外,这个问题还有一个巧妙的解法,时间复杂度只需要 O(N),不过该解法比较复杂,我个人认为没必要掌握。该算法的名字叫 Manacher’s Algorithm(马拉车算法),有兴趣的读者可以自行搜索一下。
三、手把手搞懂接雨水问题的多种解法
读完本文,可以去力扣解决如下题目:
42.接雨水(Hard)
接雨水这道题目挺有意思,在面试题中出现频率还挺高的,本文就来步步优化,讲解一下这道题:
图片
就是用一个数组表示一个条形图,问你这个条形图最多能接多少水,函数签名如下:
int trap(int[] height);
下面就来由浅入深介绍暴力解法 -> 备忘录解法 -> 双指针解法,在 O(N) 时间 O(1) 空间内解决这个问题。
一、暴力解法
对于这种问题,我们不要想整体,而应该去想局部;就像之前的文章写的动态规划问题处理字符串问题,不要考虑如何处理整个字符串,而是去思考应该如何处理每一个字符。
这么一想,可以发现这道题的思路其实很简单。具体来说,仅仅对于位置i,能装下多少水呢?
图片
能装 2 格水,因为height[i]的高度为 0,而这里最多能盛 2 格水,2-0=2。
为什么位置i最多能盛 2 格水呢?因为,位置i能达到的水柱高度和其左边的最高柱子、右边的最高柱子有关,我们分别称这两个柱子高度为l_max和r_max;位置 i 最大的水柱高度就是min(l_max, r_max)。
更进一步,对于位置i,能够装的水为:
water[i] = min(
# 左边最高的柱子
max(height[0..i]),
# 右边最高的柱子
max(height[i..end])
) - height[i]
图片这就是本问题的核心思路,我们可以简单写一个暴力算法:
int trap(vector<int>& height) {
int n = height.size();
int res = 0;
for (int i = 1; i < n - 1; i++) {
int l_max = 0, r_max = 0;
// 找右边最高的柱子
for (int j = i; j < n; j++)
r_max = max(r_max, height[j]);
// 找左边最高的柱子
for (int j = i; j >= 0; j--)
l_max = max(l_max, height[j]);
// 如果自己就是最高的话,
// l_max == r_max == height[i]
res += min(l_max, r_max) - height[i];
}
return res;
}
有之前的思路,这个解法应该是很直接粗暴的,时间复杂度 O(N^2),空间复杂度 O(1)。但是很明显这种计算r_max和l_max的方式非常笨拙,一般的优化方法就是备忘录。
二、备忘录优化
之前的暴力解法,不是在每个位置i都要计算r_max和l_max吗?我们直接把结果都提前计算出来,别傻不拉几的每次都遍历,这时间复杂度不就降下来了嘛。
我们开两个数组r_max和l_max充当备忘录,l_max[i]表示位置i左边最高的柱子高度,r_max[i]表示位置i右边最高的柱子高度。预先把这两个数组计算好,避免重复计算:
int trap(vector<int>& height) {
if (height.empty()) return 0;
int n = height.size();
int res = 0;
// 数组充当备忘录
vector<int> l_max(n), r_max(n);
// 初始化 base case
l_max[0] = height[0];
r_max[n - 1] = height[n - 1];
// 从左向右计算 l_max
for (int i = 1; i < n; i++)
l_max[i] = max(height[i], l_max[i - 1]);
// 从右向左计算 r_max
for (int i = n - 2; i >= 0; i--)
r_max[i] = max(height[i], r_max[i + 1]);
// 计算答案
for (int i = 1; i < n - 1; i++)
res += min(l_max[i], r_max[i]) - height[i];
return res;
}
这个优化其实和暴力解法思路差不多,就是避免了重复计算,把时间复杂度降低为 O(N),已经是最优了,但是空间复杂度是 O(N)。下面来看一个精妙一些的解法,能够把空间复杂度降低到 O(1)。
三、双指针解法
这种解法的思路是完全相同的,但在实现手法上非常巧妙,我们这次也不要用备忘录提前计算了,而是用双指针边走边算,节省下空间复杂度。
首先,看一部分代码:
int trap(vector<int>& height) {
int n = height.size();
int left = 0, right = n - 1;
int l_max = height[0];
int r_max = height[n - 1];
while (left <= right) {
l_max = max(l_max, height[left]);
r_max = max(r_max, height[right]);
left++; right--;
}
}
对于这部分代码,请问l_max和r_max分别表示什么意义呢?
很容易理解,l_max是height[0…left]中最高柱子的高度,r_max是height[right…n-1]的最高柱子的高度。
明白了这一点,直接看解法:
int trap(vector<int>& height) {
if (height.empty()) return 0;
int n = height.size();
int left = 0, right = n - 1;
int res = 0;
int l_max = height[0];
int r_max = height[n - 1];
while (left <= right) {
l_max = max(l_max, height[left]);
r_max = max(r_max, height[right]);
// res += min(l_max, r_max) - height[i]
if (l_max < r_max) {
res += l_max - height[left];
left++;
} else {
res += r_max - height[right];
right--;
}
}
return res;
}
你看,其中的核心思想和之前一模一样,换汤不换药。但是细心的读者可能会发现次解法还是有点细节差异:
之前的备忘录解法,l_max[i]和r_max[i]分别代表height[0…i]和height[i…n-1]的最高柱子高度。
res += min(l_max[i], r_max[i]) - height[i];
图片但是双指针解法中,l_max和r_max代表的是height[0…left]和height[right…n-1]的最高柱子高度。比如这段代码:
if (l_max < r_max) {
res += l_max - height[left];
left++;
}
图片
此时的l_max是left指针左边的最高柱子,但是r_max并不一定是left指针右边最高的柱子,这真的可以得到正确答案吗?
其实这个问题要这么思考,我们只在乎min(l_max, r_max)。对于上图的情况,我们已经知道l_max < r_max了,至于这个r_max是不是右边最大的,不重要。重要的是height[i]能够装的水只和较低的l_max之差有关:
图片
这样,接雨水问题就解决了,学会了吗?三连安排!
四、如何高效对有序数组/链表去重?
我们知道对于数组来说,在尾部插入、删除元素是比较高效的,时间复杂度是 O(1),但是如果在中间或者开头插入、删除元素,就会涉及数据的搬移,时间复杂度为 O(N),效率较低。
所以对于一般处理数组的算法问题,我们要尽可能只对数组尾部的元素进行操作,以避免额外的时间复杂度。
这篇文章讲讲如何对一个有序数组去重,先看下题目:
图片
显然,由于数组已经排序,所以重复的元素一定连在一起,找出它们并不难,但如果毎找到一个重复元素就立即删除它,就是在数组中间进行删除操作,整个时间复杂度是会达到 O(N^2)。而且题目要求我们原地修改,也就是说不能用辅助数组,空间复杂度得是 O(1)。
其实,对于数组相关的算法问题,有一个通用的技巧:要尽量避免在中间删除元素,那我就先想办法把这个元素换到最后去。
这样的话,最终待删除的元素都拖在数组尾部,一个一个 pop 掉就行了,每次操作的时间复杂度也就降低到 O(1) 了。
按照这个思路呢,又可以衍生出解决类似需求的通用方式:双指针技巧。具体一点说,应该是快慢指针。
我们让慢指针slow走左后面,快指针fast走在前面探路,找到一个不重复的元素就告诉slow并让slow前进一步。
这样当fast指针遍历完整个数组nums后,nums[0…slow]就是不重复元素,之后的所有元素都是重复元素。
图片
看下算法执行的过程:
图片
再简单扩展一下,如果给你一个有序链表,如何去重呢?其实和数组是一模一样的,唯一的区别是把数组赋值操作变成操作指针而已:
图片
对于链表去重,算法执行的过程是这样的:
图片
最后,近期准备写写一些简单实用的数组/链表技巧。那些稍困难的技巧(比如动态规划)虽然秀,但毕竟在现实生活中不容易遇到。恰恰是一些简单常用的技巧,能够在不经意间,让人发现你是个高手 _。
五、考官如何用算法调度考生的座位?
最近不是四六级考试么,我们就来聊聊 LeetCode 第 885 题,让你当考官安排座位,有趣且具有一定技巧性。这种题目并不像动态规划这类算法拼智商,而是看你对常用数据结构的理解和写代码的水平,个人认为值得重视和学习。
另外说句题外话,很多读者都问,算法框架是如何总结出来的,其实框架反而是慢慢从细节里抠出来的。希望大家看了我们的文章之后,最好能抽时间把相关的问题亲自做一做,纸上得来终觉浅,绝知此事要躬行嘛。
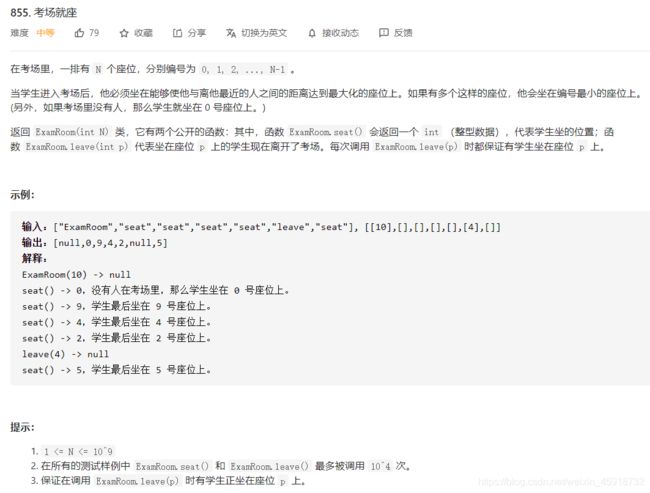
先来描述一下题目:假设有一个考场,考场有一排共N个座位,索引分别是[0…N-1],考生会陆续进入考场考试,并且可能在任何时候离开考场。
你作为考官,要安排考生们的座位,满足:每当一个学生进入时,你需要最大化他和最近其他人的距离;如果有多个这样的座位,安排到他到索引最小的那个座位,这很符合实际情况对吧。
也就是请你实现下面这样一个类:
class ExamRoom {
// 构造函数,传入座位总数 N
public ExamRoom(int N);
// 来了一名考生,返回你给他分配的座位
public int seat();
// 坐在 p 位置的考生离开了
// 可以认为 p 位置一定坐有考生
public void leave(int p);
}
比方说下面这个调用顺序,考场有 10 个座位,分别是[0…9]:
第一名考生进入时,坐在任何位置都行,但是要给他安排索引最小的位置,也就是返回位置 0。
第二名学生进入时,要和旁边的人距离最远,也就是返回位置 9。
第三名学生进入时,要和旁边的人距离最远,应该做到中间,也就是座位 4。
又进一名学生,他可以坐在座位 2 或者 6 或者 7,取最小的索引 2。
图片
座位 4 上的学生离开了。
又进来一名学生,坐在 5 号位置距离相邻的人最远。
图片
以此类推,读者肯定能够发现规律:
如果将每两个相邻的考生看做线段的两端点,新安排考生就是找最长的线段,然后让该考生在中间把这个线段「二分」,中点就是给他分配的座位。leave§其实就是去除端点p,使得相邻两个线段合并为一个。
核心思路很简单对吧,所以这个问题实际上实在考察你对数据结构的理解。对于上述这个逻辑,你用什么数据结构来实现呢?
5.1 思路分析
根据上述思路,首先需要把坐在教室的学生抽象成线段,我们可以简单的用一个大小为 2 的数组表示。
另外,思路需要我们找到「最长」的线段,还需要去除线段,增加线段。
但凡遇到在动态过程中取最值的要求,肯定要使用有序数据结构,我们常用的数据结构就是二叉堆和平衡二叉搜索树了。 二叉堆实现的优先级队列取最值的时间复杂度是 O(logN),但是只能删除最大值。平衡二叉树也可以取最值,也可以修改、删除任意一个值,而且时间复杂度都是 O(logN)。
综上,二叉堆不能满足leave操作,应该使用平衡二叉树。所以这里我们会用到 Java 的一种数据结构TreeSet,1这是一种有序数据结构,底层由红黑树维护有序性。
这里顺便提一下,一说到集合(Set)或者映射(Map),有的读者可能就想当然的认为是哈希集合(HashSet)或者哈希表(HashMap),这样理解是有点问题的。
因为哈希集合/映射底层是由哈希函数和数组实现的,特性是遍历无固定顺序,但是操作效率高,时间复杂度为 O(1)。
而集合/映射还可以依赖其他底层数据结构,常见的就是红黑树(一种平衡二叉搜索树),特性是自动维护其中元素的顺序,操作效率是 O(logN)。这种一般称为「有序集合/映射」。
我们使用的TreeSet就是一个有序集合,目的就是为了保持线段长度的有序性,快速查找最大线段,快速删除和插入。
5.2 简化问题
首先,如果有多个可选座位,需要选择索引最小的座位对吧?我们先简化一下问题,暂时不管这个要求,实现上述思路。
这个问题还用到一个常用的编程技巧,就是使用一个「虚拟线段」让算法正确启动, 这就和链表相关的算法需要「虚拟头结点」一个道理。
很重要!因为如果假想为一个线段, 左右两边的 0、(n-1)座位很难分配出去。
所以最好 虚拟线段启动。
// 将端点 p 映射到以 p 为左端点的线段
private Map<Integer, int[]> startMap;
// 将端点 p 映射到以 p 为右端点的线段
private Map<Integer, int[]> endMap;
// 根据线段长度从小到大存放所有线段
private TreeSet<int[]> pq;
private int N;
public ExamRoom(int N) {
this.N = N;
startMap = new HashMap<>();
endMap = new HashMap<>();
pq = new TreeSet<>((a, b) -> {
// 算出两个线段的长度
int distA = distance(a);
int distB = distance(b);
// 长度更长的更大,排后面
return distA - distB;
});
// 在有序集合中先放一个虚拟线段
addInterval(new int[] {
-1, N});
}
/* 去除一个线段 */
private void removeInterval(int[] intv) {
pq.remove(intv);
startMap.remove(intv[0]);
endMap.remove(intv[1]);
}
/* 增加一个线段 */
private void addInterval(int[] intv) {
pq.add(intv);
startMap.put(intv[0], intv);
endMap.put(intv[1], intv);
}
/* 计算一个线段的长度 */
private int distance(int[] intv) {
return intv[1] - intv[0] - 1;
}
「虚拟线段」其实就是为了将所有座位表示为一个线段:
图片
有了上述铺垫,主要 APIseat和leave就可以写了:
public int seat() {
// 从有序集合拿出最长的线段
int[] longest = pq.last();
int x = longest[0];
int y = longest[1];
int seat;
if (x == -1) {
// 情况一
seat = 0;
} else if (y == N) {
// 情况二
seat = N - 1;
} else {
// 情况三
【注意】这是 (x+y)/2 的防溢出写法。
seat = (y - x) / 2 + x;
}
// 将最长的线段分成两段
int[] left = new int[] {
x, seat};
int[] right = new int[] {
seat, y};
removeInterval(longest);
addInterval(left);
addInterval(right);
return seat;
}
public void leave(int p) {
// 将 p 左右的线段找出来
int[] right = startMap.get(p);
int[] left = endMap.get(p);
// 合并两个线段成为一个线段
int[] merged = new int[] {
left[0], right[1]};
removeInterval(left);
removeInterval(right);
addInterval(merged);
}
图片
三种情况
至此,算法就基本实现了,代码虽多,但思路很简单**:找最长的线段,从中间分隔成两段,中点就是seat()的返回值;找p的左右线段,合并成一个线段,这就是leave§的逻辑。**
5.3 进阶问题
但是,题目要求多个选择时选择索引最小的那个座位,我们刚才忽略了这个问题。比如下面这种情况会出错:
图片
现在有序集合里有线段[0,4]和[4,9],那么最长线段longest就是后者,按照seat的逻辑,就会分割[4,9],也就是返回座位 6。但正确答案应该是座位 2,因为 2 和 6 都满足最大化相邻考生距离的条件,二者应该取较小的。
图片
遇到题目的这种要求,解决方式就是修改有序数据结构的排序方式。具体到这个问题,就是修改TreeMap的比较函数逻辑:
pq = new TreeSet<>((a, b) -> {
int distA = distance(a);
int distB = distance(b);
// 如果长度相同,就比较索引
if (distA == distB)
return b[0] - a[0]; 【索引 由小到大,间隔由大到小。】
return distA - distB;
});
除此之外,还要改变distance函数,不能简单地让它计算一个线段两个端点间的长度,而是让它计算该线段中点到端点的长度。
private int distance(int[] intv) {
int x = intv[0];
int y = intv[1];
if (x == -1) return y;
if (y == N) return N - 1 - x;
// 中点到端点的长度
return (y - x) / 2;
}
图片
这样,[0,4]和[4,9]的distance值就相等了,算法会比较二者的索引,取较小的线段进行分割。到这里,这道算法题目算是完全解决了。
即是:修改以上两处即可。
5.4 最后总结【重点】
本文聊的这个问题其实并不算难,虽然看起来代码很多。核心问题就是考察有序数据结构的理解和使用,来梳理一下。
处理动态问题一般都会用到有序数据结构,比如平衡二叉搜索树和二叉堆,二者的时间复杂度差不多,但前者支持的操作更多。【后者 一般是删除最大值/最小值。】
既然平衡二叉搜索树这么好用,还用二叉堆干嘛呢?因为二叉堆底层就是数组,实现简单啊,详见旧文 图文详解二叉堆,实现优先级队列。 平衡二叉搜索树——你实现个红黑树试试?操作复杂,而且消耗的空间相对来说会多一些。具体问题,还是要选择恰当的数据结构来解决。
//【注意】这是 (x+y)/2 的防溢出写法。
seat = (y - x) / 2 + x;
5.5 我的题解-及- 思路
思路正确了,真的 百倍于时间。
理清思路,然后就是做!
5.5.1 思路
维护有序的座位编号
我们可以用有序集合(Java 中 TreeSet,C++ 中的 set)存储目前有学生的座位编号。当我们要调用 leave§ 函数时,我们只需要把有序集合中的 p 移除即可。当我们要调用 seat() 函数时,我们遍历这个有序集合,对于相邻的两个座位 i 和 j,如果选择在这两个座位之间入座,那么最近的距离 d 为 (j - i) / 2,选择的座位为 i + d。除此之外,我们还需要考虑坐在最左侧 0 和最右侧 N - 1 的情况。
//Java
class ExamRoom {
int N;
TreeSet<Integer> students;
public ExamRoom(int N) {
this.N = N;
students = new TreeSet();
}
public int seat() {
//Let's determine student, the position of the next
//student to sit down.
int student = 0;
if (students.size() > 0) {
//Tenatively, dist is the distance to the closest student,
//which is achieved by sitting in the position 'student'.
//We start by considering the left-most seat.
int dist = students.first();
Integer prev = null;
for (Integer s: students) {
if (prev != null) {
//For each pair of adjacent students in positions (prev, s),
//d is the distance to the closest student;
//achieved at position prev + d.
int d = (s - prev) / 2;
if (d > dist) {
dist = d;
student = prev + d;
}
}
prev = s;
}
//Considering the right-most seat.
if (N - 1 - students.last() > dist)
student = N - 1;
}
//Add the student to our sorted TreeSet of positions.
students.add(student);
return student;
}
public void leave(int p) {
students.remove(p);
}
}
复杂度分析
时间复杂度:seat() 函数的时间复杂度为 O§,其中 P是当前入座学生的数目。每次调用 seat() 函数我们都需要遍历整个有序集合。leave() 函数的时间复杂度为 O§(Python 代码中)或者 O(logP)(Java 代码中)。
空间复杂度:O§,用于存储有序集合。
5.5.2 Code-C++实现
/**
* @Description: 还原代码模板 使用 map+set 完结!
* @param {*}
* @return {*}
* @notes: 关键思路:使用seat存储已有的作为;leave擦除 seat(p) , seat则遍历 set找d==距离大 次序小。 i+d 为座次。
* 加之——额外考虑 0和N-1 加入的情况。
*/
class ExamRoom {
public:
int n;
set<int> s;
ExamRoom(int N) {
n = N;
}
int seat() {
if(s.empty()) {
s.insert(0);
return 0;
}
int space = 0, insertPos = -1;
int findFirst = -1;
for(int a:s){
if(findFirst == -1){
findFirst = a;
// 0
if( s.count(0) == 0 ){
space = a - 0;
insertPos = 0;
}
continue;
}
if( ceil((a - findFirst)/2) > space ){
space = ceil((a - findFirst)/2);
insertPos = findFirst + space;
}
findFirst = a;
}
// n-1
if(s.count(n-1) == 0){
if( n-1-findFirst > space ){
space = n-1-findFirst;
insertPos = n-1;
}
}
s.insert(insertPos);
return insertPos;
}
void leave(int p) {
s.erase(p);
}
};
5.6 D.S.大总结—考察对于数据结构基础的 熟练程度.
因为真的是一些基础的已经现存的 数据结构,可以直接使用!
红黑树参考网站:红黑树详解以及与BST和AVL树的比较
书籍:《算法》第四版(红宝书) P273
六、如何拆解复杂问题:实现一个计算器
我记得很多大学数据结构的教材上,在讲栈这种数据结构的时候,应该都会用计算器举例,但是有一说一,讲的真的垃圾,我只感受到被数据结构支配的恐惧,丝毫没有支配数据结构的快感。
不知道多少未来的计算机科学家就被这种简单的数据结构劝退了。
图片
那么,我们最终要实现的计算器功能如下:
1、输入一个字符串,可以包含+ - * / ()、数字、空格,你的算法返回运算结果。
2、要符合运算法则,括号的优先级最高,先乘除后加减。
3、除号是整数除法,无论正负都向 0 取整(5/2=2,-5/2=-2)。
4、可以假定输入的算式一定合法,且计算过程不会出现整型溢出,不会出现除数为 0 的意外情况。
比如输入如下字符串,算法会返回 9:
3 * (2-6 /(3 -7))
可以看到,这就已经非常接近我们实际生活中使用的计算器了,虽然我们以前肯定都用过计算器,但是如果简单思考一下其算法实现,就会大惊失色:
1、按照常理处理括号,要先计算最内层的括号,然后向外慢慢化简。这个过程我们手算都容易出错,何况写成算法呢!
2、要做到先乘除,后加减,这一点教会小朋友还不算难,但教给计算机恐怕有点困难。
3、要处理空格。我们为了美观,习惯性在数字和运算符之间打个空格,但是计算之中得想办法忽略这些空格。
那么本文就来聊聊怎么实现上述一个功能完备的计算器功能,关键在于层层拆解问题,化整为零,逐个击破,相信这种思维方式能帮大家解决各种复杂问题。
下面就来拆解,从最简单的一个问题开始。
6.1 字符串转整数
是的,就是这么一个简单的问题,首先告诉我,怎么把一个字符串形式的正整数,转化成 int 型?
string s = “458”;
int n = 0;
for (int i = 0; i < s.size(); i++) {
char c = s[i];
n = 10 * n + (c - ‘0’);
}
// n 现在就等于 458
这个还是很简单的吧,老套路了。但是即便这么简单,依然有坑:(c - ‘0’)的这个括号不能省略,否则可能造成整型溢出。
因为变量c是一个 ASCII 码,如果不加括号就会先加后减,想象一下n如果接近 INT_MAX,就会溢出。所以用括号保证先减后加才行。
6.2 处理加减法
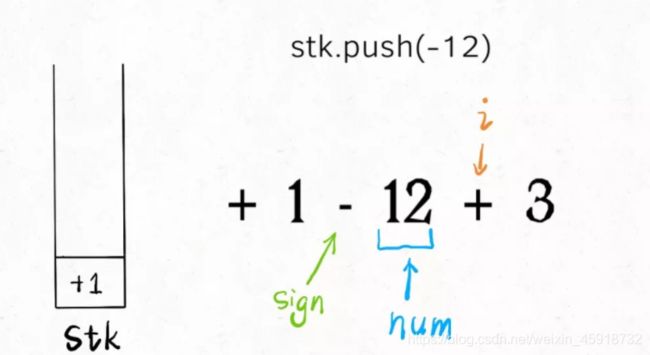
现在进一步,如果输入的这个算式只包含加减法,而且不存在空格,你怎么计算结果?我们拿字符串算式1-12+3为例,来说一个很简单的思路:
1、先给第一个数字加一个默认符号+,变成+1-12+3。
2、把一个运算符和数字组合成一对儿,也就是三对儿+1,-12,+3,把它们转化成数字,然后放到一个栈中。
3、将栈中所有的数字求和,就是原算式的结果。
我们直接看代码,结合一张图就看明白了:
int calculate(string s) {
stack<int> stk;
// 记录算式中的数字
int num = 0;
// 记录 num 前的符号,初始化为 +
char sign = '+';
for (int i = 0; i < s.size(); i++) {
char c = s[i];
// 如果是数字,连续读取到 num
if (isdigit(c))
num = 10 * num + (c - '0');
// 如果不是数字,就是遇到了下一个符号,
// 之前的数字和符号就要存进栈中
if (!isdigit(c) || i == s.size() - 1) {
switch (sign) {
case '+':
stk.push(num); break;
case '-':
stk.push(-num); break;
}
// 更新符号为当前符号,数字清零
sign = c;
num = 0;
}
}
// 将栈中所有结果求和就是答案
int res = 0;
while (!stk.empty()) {
res += stk.top();
stk.pop();
}
return res;
}
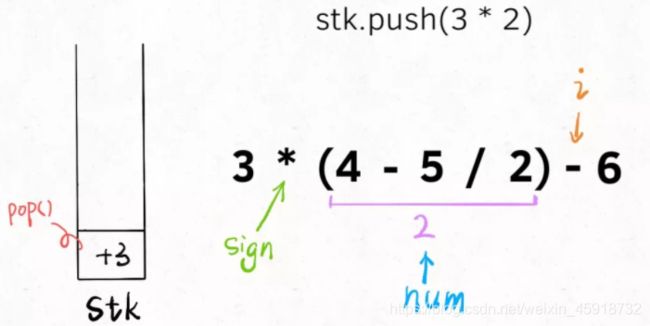
我估计就是中间带switch语句的部分有点不好理解吧,i就是从左到右扫描,sign和num跟在它身后。当s[i]遇到一个运算符时,情况是这样的:
所以说,此时要根据sign的 case 不同选择nums的正负号,存入栈中,然后更新sign并清零nums记录下一对儿符合和数字的组合。
另外注意,不只是遇到新的符号会触发入栈,当i走到了算式的尽头(i == s.size() - 1),也应该将前面的数字入栈,方便后续计算最终结果。
至此,仅处理紧凑加减法字符串的算法就完成了,请确保理解以上内容,后续的内容就基于这个框架修修改改就完事儿了。
6.3 处理乘除法
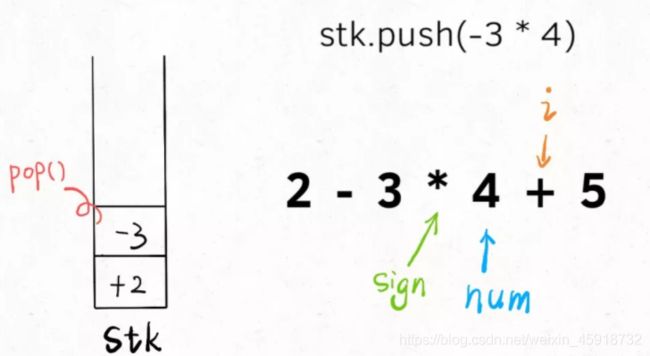
其实思路跟仅处理加减法没啥区别,拿字符串2-3*4+5举例,核心思路依然是把字符串分解成符号和数字的组合。
比如上述例子就可以分解为+2,-3,*4,+5几对儿,我们刚才不是没有处理乘除号吗,很简单,其他部分都不用变,在switch部分加上对应的 case 就行了:
for (int i = 0; i < s.size(); i++) {
char c = s[i];
if (isdigit(c))
num = 10 * num + (c - '0');
if (!isdigit(c) || i == s.size() - 1) {
switch (sign) {
int pre;
case '+':
stk.push(num); break;
case '-':
stk.push(-num); break;
// 只要拿出前一个数字做对应运算即可
case '*':
pre = stk.top();
stk.pop();
stk.push(pre * num);
break;
case '/':
pre = stk.top();
stk.pop();
stk.push(pre / num);
break;
}
// 更新符号为当前符号,数字清零
sign = c;
num = 0;
}
}
乘除法优先于加减法体现在,乘除法可以和栈顶的数结合,而加减法只能把自己放入栈。
现在我们思考一下如何处理字符串中可能出现的空格字符。其实也非常简单,想想空格字符的出现,会影响我们现有代码的哪一部分?
// 如果 c 非数字
if (!isdigit(c) || i == s.size() - 1) {
switch (c) {
...}
sign = c;
num = 0;
}
显然空格会进入这个 if 语句,但是我们并不想让空格的情况进入这个 if,因为这里会更新sign并清零nums,空格根本就不是运算符,应该被忽略。
那么只要多加一个条件即可:
if ((!isdigit(c) && c != ' ') || i == s.size() - 1) {
...
}
好了,现在我们的算法已经可以按照正确的法则计算加减乘除,并且自动忽略空格符,剩下的就是如何让算法正确识别括号了。
6.4 处理括号
处理算式中的括号看起来应该是最难的,但真没有看起来那么难。
为了规避编程语言的繁琐细节,我把前面解法的代码翻译成 Python 版本:
def calculate(s: str) -> int:
def helper(s: List) -> int:
stack = []
sign = '+'
num = 0
while len(s) > 0:
c = s.pop(0)
if c.isdigit():
num = 10 * num + int(c)
if (not c.isdigit() and c != ' ') or len(s) == 0:
if sign == '+':
stack.append(num)
elif sign == '-':
stack.append(-num)
elif sign == '*':
stack[-1] = stack[-1] * num
elif sign == '/':
# python 除法向 0 取整的写法
stack[-1] = int(stack[-1] / float(num))
num = 0
sign = c
return sum(stack)
# 需要把字符串转成列表方便操作
return helper(list(s))
这段代码跟刚才 C++ 代码完全相同,唯一的区别是,不是从左到右遍历字符串,而是不断从左边pop出字符,本质还是一样的。
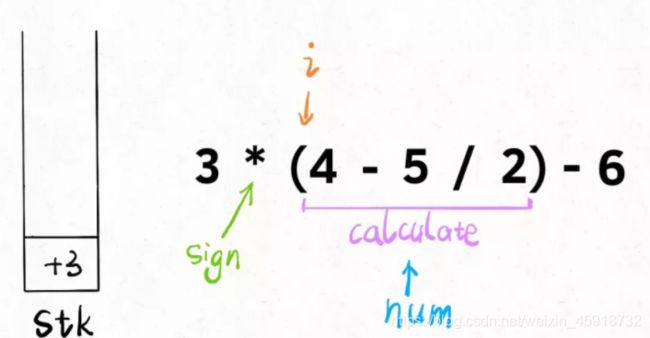
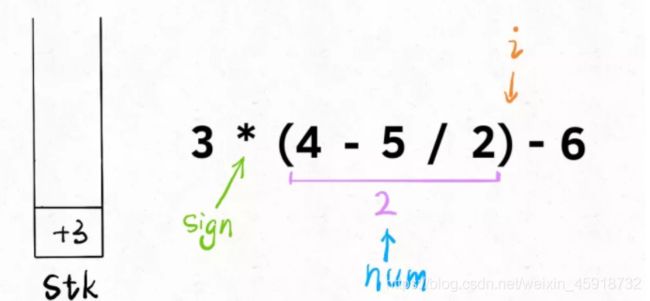
那么,为什么说处理括号没有看起来那么难呢,因为括号具有递归性质。我们拿字符串3*(4-5/2)-6举例:
calculate(3*(4-5/2)-6)
= 3 * calculate(4-5/2) - 6
= 3 * 2 - 6
= 0
可以脑补一下,无论多少层括号嵌套,通过 calculate 函数递归调用自己,都可以将括号中的算式化简成一个数字。换句话说,括号包含的算式,我们直接视为一个数字就行了。
现在的问题是,递归的开始条件和结束条件是什么?遇到(开始递归,遇到)结束递归:
def calculate(s: str) -> int:
def helper(s: List) -> int:
stack = []
sign = '+'
num = 0
while len(s) > 0:
c = s.pop(0)
if c.isdigit():
num = 10 * num + int(c)
# 遇到左括号开始递归计算 num
if c == '(':
num = helper(s)
if (not c.isdigit() and c != ' ') or len(s) == 0:
if sign == '+': ...
elif sign == '-': ...
elif sign == '*': ...
elif sign == '/': ...
num = 0
sign = c
# 遇到右括号返回递归结果
if c == ')': break
return sum(stack)
return helper(list(s))
你看,加了两三行代码,就可以处理括号了,这就是递归的魅力。至此,计算器的全部功能就实现了,通过对问题的层层拆解化整为零,再回头看,这个问题似乎也没那么复杂嘛。
6.5 最后总结
本文借实现计算器的问题,主要想表达的是一种处理复杂问题的思路。
我们首先从字符串转数字这个简单问题开始,进而处理只包含加减法的算式,进而处理包含加减乘除四则运算的算式,进而处理空格字符,进而处理包含括号的算式。
可见,对于一些比较困难的问题,其解法并不是一蹴而就的,而是步步推进,螺旋上升的。 如果一开始给你原题,你不会做,甚至看不懂答案,都很正常,关键在于我们自己如何简化问题,如何以退为进。
退而求其次是一种很聪明策略。 你想想啊,假设这是一道考试题,你不会实现这个计算器,但是你写了字符串转整数的算法并指出了容易溢出的陷阱,那起码可以得 20 分吧;如果你能够处理加减法,那可以得 40 分吧;如果你能处理加减乘除四则运算,那起码够 70 分了;再加上处理空格字符,80 有了吧。我就是不会处理括号,那就算了,80 已经很 OK 了好不好。
我们要支配算法,而不是被算法支配。