R语言及参考答案（2）

所有题目的参考答案在我的资源里面—>>>R语言与统计性描述题目及参考答案

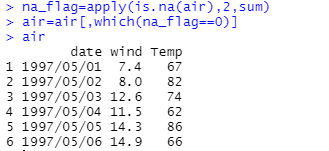
1.有一个数据框，其生成代码如下，
Ozone <- c(41, 36, 12, 18, NA, 28)
Solar.R <- c(190, 118, 149, 313, NA, NA)
wind <- c(7.4, 8.0, 12.6, 11.5, 14.3, 14.9)
Temp <- c(67, 82, 74, 62, 86, 66)
date <-c(“1997/05/01”,“1997/05/02”,“1997/05/03”,“1997/05/04”, “1997/05/05”,“1997/05/06”)
air <- data.frame(date,Ozone,Solar.R,wind,Temp, stringsAsFactors = FALSE)
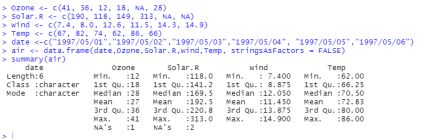
（1）使用 summary（）函数查看哪一列含有缺失值的个数，并查看 ‘wind’列的最大值。

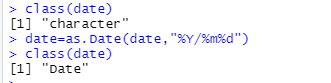
（2）使用 class（）函数查看 date 的类型，并将其转化为 date 型，格式为 年/月/日。

（3）使用 subset（）根据 ‘Temp’ 列获取 air 中 ‘Temp’ 大于 60 小于 70 的数据。

（4）将 air 中含有缺失值的列去掉。

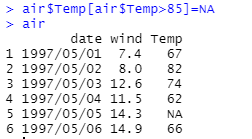
（5）找出 ‘Temp’ 中大于 85 的值将其设置为缺失值。

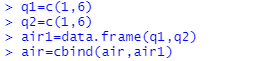
（6）创建一个数据框 air1 包含两个列 q1，q2。用 cbind 函数添加到 air 中。

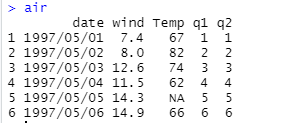
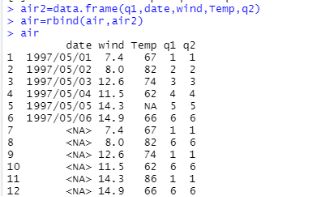
（7）使用 names（） 函数查看 air 的列名，并根据列自己创建一个数据框。使用 rbind（） 函数添加到 air 中

2.使用程序包DAAG中的数据集tinting,

（1)获得变量‘tint’和‘sex’的列联表;

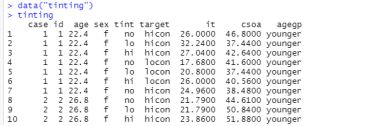
（2)在同一图上作出变量 ‘sex’与‘tint’的联合柱状图;

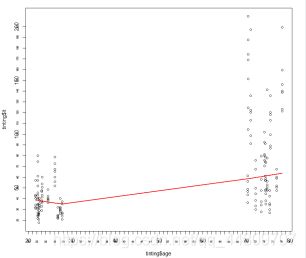
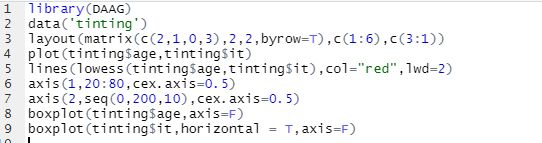
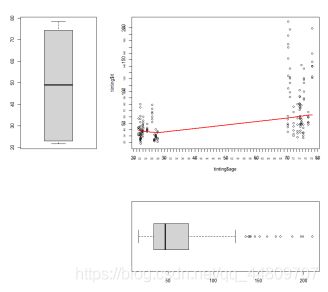
（3) 作出‘age’和‘it’的散点图, 并进一步完成下面的操作:
i. 用lowess()函数作出拟合线;

ii. 在图的两个坐标轴上加上更细小的刻度;

iii. 在图的两个坐标轴上加上箱型图.

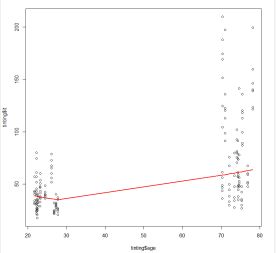
（4) 作出‘age’和‘it’关于因子变量‘tint’的条件散点图;

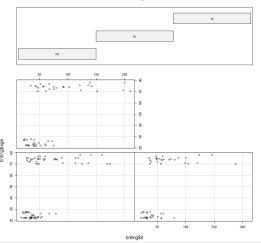
（5)作出‘age’和‘it’关于因子变量‘tint’和‘sex’的条件散点图;

（6)做出‘it’与‘csoa’的等高线图;

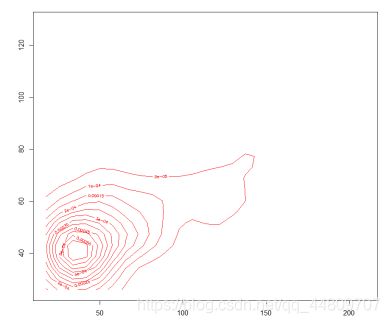
（7)使用matplot( )描述变量‘age’,‘it’和‘csoa’.

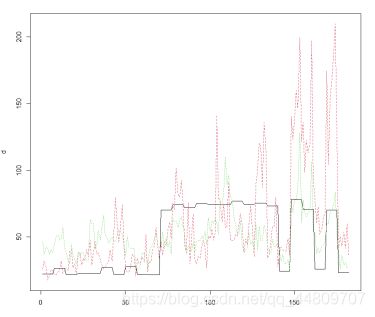
3. 一个复杂系统由100个相互独立的元件组成，在系统运行时每个元件损坏的概率为0.1，为使系统正常工作，至少必须有85个元件工作，求系统的可靠度(正常工作的概率)
   

4. 考虑两个大的且相互独立的奶牛群。在牛群A中，假定牛奶产量服从平均产量为40磅、标准差为5磅的正态分布。牛群B服从产奶量平均值为36磅、标准差为8磅的正态分布。一位乳品科学家将大的产奶量定义为至少48磅。请问从哪个牛群中随机挑选母牛更有可能获得大产奶量？请提供用R语言分析本题的过程。
   、
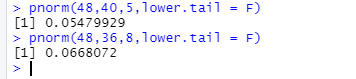   从B牛群中挑选更有可能获得更大产奶量。

参考答案在我的资源里面：R语言与统计性描述题目及参考答案

【作业】
1.1 我们以大马哈鱼为例。执行下列操作：
a.生成一些如下的人工数据：100个正态分布的随机数(即长度为100的向量)，该正态分布满足均值为42.0以及标准差为6.3的条件。将该向量命名为‘weight’(即大马哈鱼的重量)并输出它的前25个值。

b.计算并输出‘weight’向量的均值、中位数、值域、标准差以及该向量的图基五数总括（Tukey’s five-number summary）。

c.生成一个‘weight’向量的直方图。要求直方图中的柱状体为蓝色，并且x轴对应的标签为‘Salmon Weight(lbs.)

d.生成‘weight’向量的箱线图。要求y轴对应的标签为‘Salmon Weight (lbs.)’，设置颜色为蓝色，看看会出现什么。

e.在你看来，操作c,d中对于‘weight’向量分别绘制的两种图，哪种图生成了更多信息？(不超过70字)
我觉得箱线图生成了更多的信息。从箱线图中可以看到数据的最值以及中位数和两个四分位数，而我们在直方图中仅仅可以看到数据的一个范围。
1.2 使用大马哈鱼的长度来估计它自身的重量
a.分别输入下列数据，将第一组数据命名为‘length1’的向量，第二组数据命名为‘weight1’。
Length (inches): 10 20 30 40 50 60
Weight (lbs): 0.4 2.4 9.5 21.0 38.7 74.0

b.使用散点图绘制数据。x轴对应标签为‘Length’，y轴为‘Weight’。

c.定性描述b中绘制的散点图的趋势。(不超过25个字)
weigh随length的增加而增加，指数递增。
d.使用散点图再绘制数据一次(本次要求对散点图中的自变量和因变量求对数。提示：对两个变量使用log()函数，且均放在plot()命令中作为参数)。

e.描述d中散点图的趋势(不超过25个字)
weight随着 length增长而增长，线性增长
1.3生成一个因子(类别)变量，其长度为100，分为5个因子水平(每个因子水平20个值)分别对应着以下5条河流：“Egegik” “Cinder” “Igushik” “Kvichak” “Meshik”
a.将因子变量命名为‘river’，并将‘river’与第1题中的‘weight’向量合并到一个命名为‘bristol.df’的数据框(data frame)中。使用rm（）函数将‘river’和‘weight’变量移除。

b.将‘bristol.df’作为参数，调用summary（）函数并输出结果。

c.将‘bristol.df’作为参数，调用str（）函数并输出结果。

d.生成一个名为river的计数表。

e.为每条河流中大马哈鱼的重量数据绘制一个箱线图。

2. 由命令

data(InsectSprays)
InsectSprays
得到数据集InsectSprays, 根据数据作出有意义的图, 并对数据作出描述
性统计.

3. Felix是只喜欢捉老鼠的猫，它每天成功捕获至少一只老鼠的概率是0.6。假设他狩猎成功的概率每天都是独立的。我们仔细观察了他四天，请问Felix四天狩猎成功的概率为0.0256吗？请首先列出你动手计算的解题过程，再列出用R语言求解的过程。
   捕获不到老鼠的概率为0.4，四次都没狩猎成功则为0.4的四次方，根据题意得到这四天内狩猎成功的概率为1-p（失败）

4. 有绿色和红色两种硬币，已知绿色硬币正面朝上的概率为0.5，而红色硬币正面朝上的概率为0.8。请用R语言计算下列题目。
   a. 绿色硬币独立掷两次，红色硬币独立掷两次。假设绿色和红色硬币的投掷事件彼此独立。请计算出两枚硬币正面朝上总数为3的概率。

b. 令X为投掷硬币4次的正面总数。求出X的概率分布。

c. 求X的期望和方差

5. 本题目旨在让同学考虑违反“二项分布”假设情况下的影响。在一次掷硬币试验中，第一次投掷硬币正面和反面朝上的可能性均为0.5，第一次投掷硬币后每次正、反面朝上的概率取决于前一次获得的结果。如果前一次的结果是正面朝上，则即将发生的投掷硬币事件正面朝上的概率为0.75。如果前一次的结果是反面朝上，则即将发生的投掷硬币事件反面朝上的概率为0.75。硬币总共投掷了3次，请用R语言计算以下题目。
   a. 设X =正面朝上的次数。试求X的概率分布。

b. 如果连续投掷三次硬币，分别求出第一次、第二次和第三次投掷硬币导致出现正面朝上的概率。

c. 如果前一次投掷硬币结果与接下来投掷硬币结果相同的发生概率为0.9而不是0.75。试求解（a）和（b）两题。

d. 请将此事件与严格遵守二项分布的硬币投掷试验进行比较，此事件是否违反了二项分布（三条）假设？如果有，请解释是哪几条？说明原因。
不违背，每次成功概率都是0.5
6. 设Z〜N（0,1）。请使用（i）查表法；（ii）R功能；（iii）R模拟(通过产生的随机数求得) 来计算以下概率。
a. P(Z ≤ 0.82)
（i）0.7939
(ii)
(iii)
b. P(-0.74 ≤ Z ≤ 0.82)
（i）p（0.82）=0.7939，p（-0.74）=1-0.7703=0.2297
P（0.74≤Z≤0.82）=0.7939-0.2297=0.5642

(ii)
(iii)

c. P(-0.6 ≤ Z ≤0.9)
（i）p（0.9）=0.8159，p（-0.6）=1-0.7257=0.2743
P（-0.6≤Z≤0.9）=0.8159-0.2743=0.541
(ii)
(iii)

d. P(-0.614 ≤ Z)
（i）P（-0.614≤Z）=1-p（z≤0.614）=1-（1-p（0.614））=0.7291
(ii)
(iii)

7.令X为从松树上随机选择的松针的长度。已知X服从正态分布，方差为0.5 cm2。还已知90％的松针长度短于4.1cm。请用R语言计算下列题目。
a. 随机挑选一根松针其长度大于2.9cm的概率是多少？

b. 假设随机收集了75根松针，对于每个松针，我们注意到其长度总不等于4.1厘米。令Y为这75根松针样品中短于4.1cm松针的集合，请计算Y的方差是多少？

参考答案在我的资源里面—>>>R语言与统计性描述题目及参考答案