1.基本概念
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。
回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
2.基本思想
在包含问题的所有解的解空间树中,按照有限搜索的策略,从根节点出发深度探索解空间树。当探索到某一接点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索,如果该结点不包含问题的解,则逐层想其祖先结点回溯。(回溯法就是对隐式的深度优先搜索算法)
若用回溯法求解问题的所有解时,要回溯到根,且根节点的所有可行的子树都已经被所有遍才结束。而使用回溯法求解任一个解时,只要搜索到问题的一个解就可以结束。
3.解空间的树结构
使用回溯法的解空间一般有两种解空间:子集树和排列树
3.1子集树
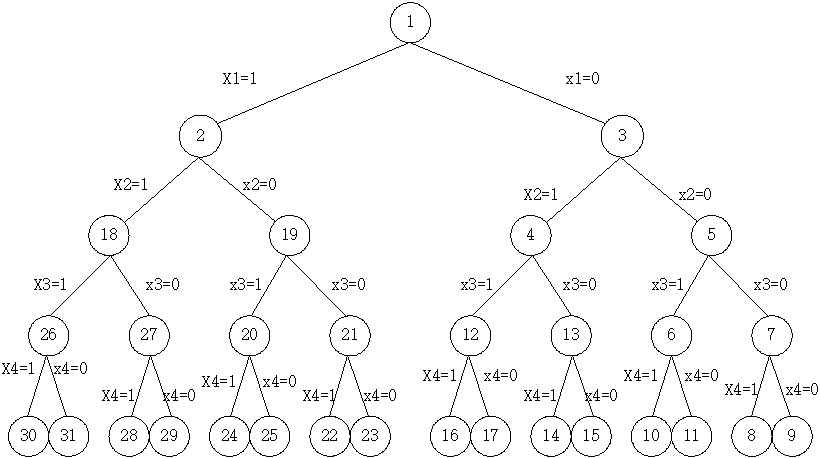
当所给的问题从n个元素的集合S中找出满足某种性质的子集时,相应的解空间树称为子集树。常用于0-1问题,如0-1背包问题。
如下图:
3.2排列树
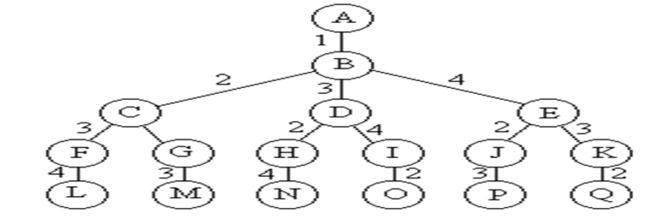
当所给的问题是确定n个元素满足某种性质的排列时,相应的解空间树称之为排列树。排序树通常有n!叶结点。
如下图:
4.用回溯法解题的一般步骤
- 针对所给问题,确定问题的解空间:
首先明确定义问题的解空间,问题的解空间应该至少包含问题的一个解 - 确定结点扩展搜索规则
- 以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索
5.算法框架
1.问题框架
设问题的解是一个n维向量(a1,a2,………,an),约束条件是ai(i=1,2,3,…..,n)之间满足某种条件,记为f(ai)。
2.递归回溯框架
回溯法是对解空间的深度优先搜索,在一般情况下使用递归函数来实现回溯法比较简单,其中i为搜索的深度,框架如下:
void backtrack (int t) //t表示递归深度
{
if (t>n) output(x); //n表示深度界限
else
for (int i=f(n,t);i<=g(n,t);i++) // f(n,t),g(n,t)分别表示当前扩展结点未搜索过的子树的起始编号和终止编号
{
x[t]=h(i);
if (constraint(t)&&bound(t)) //满足约束函数和限界函数
backtrack(t+1);
}
}
3.非递归的算法框架
void iterativeBacktrack ()
{
int t=1;
while (t>0) {
if (f(n,t)<=g(n,t))
for (int i=f(n,t);i<=g(n,t);i++) {
x[t]=h(i);
if (constraint(t)&&bound(t)) {
if (solution(t)) output(x);
else t++;}
}
else t--;
}
}
6.举个例子
现在举个例子,给定一组数组nums,再给定一个目标值target,找出集合nums的所有子集使其之和刚好为目标值,nums中的数只能使用一次。
例如:给定数组nums = {1,2,3,4,5},给定目标值target = 9,那么所能得到的结果有:
[0, 1, 1, 1, 0]
[0, 0, 0, 1, 1]
也即是:2+3+4和4+5
现在我们来考虑一下如何求解这个题,要找出所有子集,这显然有点“穷举搜索”的感觉,回溯就是这样一种“搜索”算法。
那么按照回溯步骤:
6.1 确定问题的解空间
用0/1表示是否是用集合中某个元素,那么对于整个集合,我们可以定义一个数组x,x[i]=0,则表示不使用第i个元素;x[i]=1,表示是用该元素。这样就将问题转化问了经典的0-1问题,而二叉树天然具有这样的性质(左子树对应1,右子树对应0,当然也可以反过来定义)。构造出的解空间树如上文中的子集树。这里就不赘述了。
6.2 确定结点扩展搜索规则
这个没什么好说的,大多数回溯问题均使用深度遍历。
6.3 进行搜索,必要时加入剪枝函数
什么是剪枝函数?其实这是一个很形象的名词,在上文中我们构造了一个解空间树,那么这颗树就有很多分支。在搜索过程中,我们可以将一些明显不可能产生解的分支给去掉,降低搜索次数。如果我们不使用剪枝函数,那么就会全部进行遍历,这往往不是我们想要的。
首先贴上不加剪枝函数的代码:
import java.util.Arrays;
public class Main {
/**
* 回溯法
*
*/
static int[] nums = {1,2,3,4,5};
static int target = 9;
static int n = nums.length;
static int[] currentX = new int[n];
public static void main(String[] args) {
backTrack(0);
}
static int iter = 0;
static void backTrack(int i ) {
if(i == n) {
//结束
return;
}
//求和
int currentSum = sum(currentX);
if(currentSum+nums[i] < target) {
//满足约束条件
currentX[i] = 1;
backTrack(i+1);
}else if(currentSum+nums[i] == target) {
//满足约束条件
currentX[i] = 1;
System.out.println(Arrays.toString(currentX));
return;
}
//准备进入右子树,不一定能进入
currentX[i] = 0;
//不满足约束条件,加入剪枝函数,减低遍历次数
//设计规则:当前和只加上右子树的最大值都无法达到target,则不用进入右子树
// if(currentSum + bound(i+1) >= target) {
System.out.println(++iter);
backTrack(i+1);
//}
}
static int bound(int i) {
int sum = 0;
for(;i这里我将代码中的剪枝函数注释掉了,下面是运行结果:
1
2
3
4
5
6
7
8
9
[1, 0, 1, 0, 1]
10
11
12
13
[0, 1, 1, 1, 0]
14
15
16
17
18
19
20
21
[0, 0, 0, 1, 1]
22
23
进入右子树23次,一共有三个解。
现在我们将注释删掉,运行结果如下:
1
2
3
4
[1, 0, 1, 0, 1]
5
6
7
[0, 1, 1, 1, 0]
8
9
10
11
[0, 0, 0, 1, 1]
可以看到,进入右子树的次数只有11次了,也就是加入剪枝函数后,我们的搜索次数减少了12次。显然这是很可观。
7.最后
回溯法的介绍大概就这么多了,回溯法能够找到所有满足约束条件的解,还有一种常用求解优化问题的算法-分支限界法,用来求解满足约束条件的一个解。