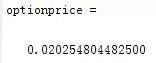首先我们来看一个条款:
这是建信基金发布的建信策略分级其中的不定期下折,当分级B,也就是所谓的建信进取份额净值达到0.2元之后会触发下折,出发下折的时候,参照条款收益,如果是在折价状态下,折价部分将会化作百分之七十五母基金收益。反之溢价,收益和亏损会处于镜面反射的状态。
接着我们来思考一个问题,这个条款的价值跟什么因素有关?
首先是B份额的净值,毫无疑问这是一个触发点,等同于控制开关,接着就是A的价格,当A在下折日价格小于1元的之后就会产生收益。最后是条款存活时间,也就是期权到期时间。
跟传统欧式期权或者美式期权不同的是,这个条款没有到规定时间行权的条件,也没有随时行权的条件,只有敲入位置强制行权。
而且,这类条款参考的标的资产有两类,所以很难得到解析解。
下面示范一下用蒙特卡洛模拟做的定价。
首先我们需要模拟一个标准正态分布构成的二元正态分布,关键参数是协方差:
rx=ones(40000,4000);
for i=1:2:3999
mu=[0 0];
cov=[1,0.0045;0.0045,1];
aa = mvnrnd(mu,cov,num1);
rx(:,i:i+1)=aa;
end
rxA=rx(:,1:2:end-1);
rxB=rx(:,2:2:end);
SA = [priceA*ones(num1,1) zeros(num1,1/deltaT)];
NB = [NevB*ones(num1,1) zeros(num1,1/deltaT)];
上面这段程序就是模拟出一个二元正态分布曲面结构,假定分级A的价格和分级B的净值在上面进行随机游走。注意的是,我们需要同时生成AB的路径,所以rx数组中奇数位置是A的路径,偶数位置是B的路径。
现在做400000次随机游走,参考的模型是:
其中需要注意,u不能用历史收益拟合,在风险中性测度下表现为统一对比的资产融资标的,也就是融资成本,可以定义为shibor三月指数。
代码如下:
%-------------------------模拟分级A的路径-----------------------%
for i=1:1/deltaT
SA(:,i+1) = SA(:,i).*exp((r-sigmaA^2/2)*deltaT+sigmaA*deltaT^0.5*rxA(:,i));
end
%--------------------------------------------------------------%
%-------------------------模拟分级B的路径-----------------------%
for i=1:1/deltaT
NB(:,i+1) = NB(:,i).*exp((r-sigmaB^2/2)*deltaT+sigmaB*deltaT^0.5*rxB(:,i));
end
%--------------------------------------------------------------%
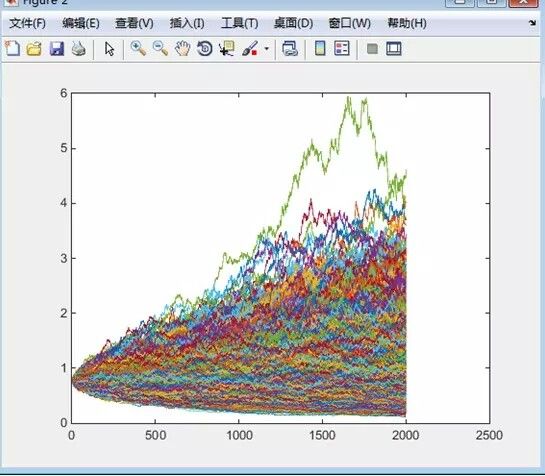
那么模拟出来的路径是怎么样的呢?
如图:
之后,做400000次筛选,如果在二元路径下触碰到敲入点的位置,那么强制行权,收益以对数的形式贴现到起初,代码如下:
for i=1:1:length(NB(:,1))
u=find(NB(i,:)<=0.25);
if isempty(u)==1;
GG=1;
time=0;
else
GG=SA(i,u(1));
time=u(1);
end
payoff(i,:)=(1-GG)*0.75*exp(-r*time*deltaT);
end
optionprice=sum(payoff)/length(payoff)
最后,就可以收敛与一个数值附近,这就是用随机模拟的二元资产期权的数值解。
参数前置:
r = 0.025;T = 1;deltaT = 1/2000;sigmaA = 0.37;sigmaB=0.45;%ltaT这里指把整个时间区间划分为按deltaT间隔的区间,指该频率的所有数据长度
priceA =0.93; %当前价格
NevB =0.37;