基于DCT变换的JPEG图像压缩

基于DCT变换的JPEG图像压缩

摘 要：图像和视频通常在计算机中表示会占用非常大的空间，而出于节省硬盘空间的考虑，往往要进行压缩。而随着网络的发展，图像压缩技术越来越被人所重视。DCT变换是图像压缩的一项重要技术，本文主要对基于DCT变换的JPEG图像压缩进行研究，并用Matlab进行了算法仿真。实验结果表明, JPEG压缩算法实现简单，在很大的压缩范围内，都能得到很好的重建图像质量。
关键词：DCT变换；JPEG图像；压缩

  图像和视频通常在计算机中表示后会占用非常大的空间，而出于节省硬盘空间的考虑，往往要进行压缩。同时，传输过程中，为了节省珍贵的带宽资源和节省时间，也迫切要求压缩。图像编码与压缩从本质上来说就是对要处理的图像数据按一定的规则进行变换和组合，从而达到以尽可能少的代码（或符号）来表示尽可能多的数据信息。图像压缩可分为有损压缩和无损压缩，尽管人们总希望能对图像进行无损压缩，但通常有损压缩的压缩比比无损压缩的高，更易于传输.基于离散余弦变换（DCT，Discrete Cosine Transform）的图像压缩是有损压缩算法，它应用于绝大多数图像压缩场合，并且它能在图像的压缩操作中获得较高的压缩比，压缩后还原得到的图像与原始图像相比较，重构图像与原图像的视觉效果基本相同，因而得到了广泛的应用，因此，本文以基于DCT的二维JPEG图像压缩为主要研究内容，通过软件仿真实现分析实验结果得出结论。

1. JPEG标准

  JPEG（Joint Photographic Experts Group）是在国际标准化组织(ISO)领导之下制定静态图像压缩标准的委员会，第一套国际静态图像压缩标准ISO 10918-1(JPEG)就是该委员会制定的。1992年，JPEG被正式采纳为国际标准。

2. JPEG压缩编码

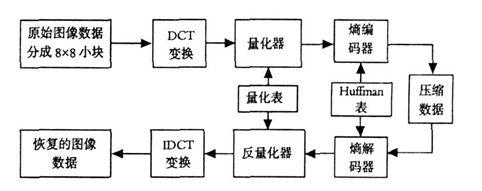
JPEG 压缩算法基本流程如图 1 所示, 压缩编码过程包括图像数据分块 、DCT 变换、量化、Huffman编码四个步骤。

图1 JPEG 压缩算法基本流程

  即首先将要压缩的图像a分割成一定的8×8像素的图像子块，再用离散余弦变换（DCT）将子块变为8×8的DCT系数阵列；然后用一个8×8的量化值阵列对这些系数进行量化；最后用熵编码器将量化后的系数编码成一串比特数据流.经过传输或存储，比特数据流经过熵解码器进行解码，重新生成一组量化了的DCT系数，使用与编码时相同的量化值阵列对这些量化了的系数进行反量化，利用反向离散余弦变换（IDCT）将此8×8DCT系数阵列变换成空间域的8×8图像子块，最后将反变换后的组合成一幅图像.这样完成了一幅图像的压缩与解压过程。

2.1 DCT变换

  DCT变换利用了傅里叶变换的对称性，变换后的结果只包含余弦项。虽然变换的种类很多，比如DCT，DFT、KLT、WHT等，但从变换后能量集中从好到劣的排列顺序KLT，DCT，DFT，WHT和运算量从小到大的排列顺序WHT，DCT、DFT，KLT来看，DCT的压缩能力与KLT最佳变换相近，计算量适中，性能优于DFT，WHT等其他变换。同时，相对于KLT而言，DCT具有固定的基和物理含义，更易于实现，因此DCT变换成为变换编码的首选。
  二维离散余弦变换的正变换公式为：
$$F(u,v)=\frac{1}{N}C(u)C(v)\sum _{x=0}^{N-1}\sum _{y=0}^{N-1}f(x,y)\mathrm{cox}\left(\frac{u\pi (2x+1)}{2N}\right)\mathrm{cox}\left(\frac{v\pi (2y+1)}{2N}\right)$$

  反变换的表达式为：
$$f(x,y)=\frac{1}{N}\sum _{x-0}^{N-1}\sum _{y=0}^{N-1}C(u)C(v)F(u,v)\mathrm{cox}\left(\frac{u\pi (2x+1)}{2N}\right)\mathrm{cox}\left(\frac{v\pi (2y+1)}{2N}\right)$$

  在图像的压缩编码中，N一般取8。
  以上各式中的系数：

$$\{\begin{array}{ll}C(u),C(v)=\frac{1}{\sqrt{N}}& \text{ 当 }u,v=0\\ C(u),C(v)=\sqrt{\frac{2}{N}}& \text{ 其它 }\end{array}$$

2.2 量化

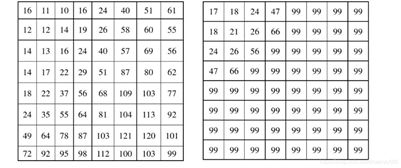
  对经过FDCT变换后的频率系数进行量化。量化的目的是减小非“0”系数的幅度以及增加“0”值系数的数目。JPEG使用的颜色是YUV格式，其中Y分量代表了亮度信息，UV分量代表了色差信息。因为人眼对亮度信号比对色差信号更敏感，因此使用了两种量化表（图2）：亮度量化值和色差量化值。此外，由于人眼对低频分量的图像比对高频分量的图像更敏感，因此图中的左上角的量化步距要比右下角的量化步距小。由于量化表的左上角的值较小，右上角的值较大，这样就起到了保持低频分量，抑制高频分量的目的。

图2：量化表（左图为亮度量化步长表，右图为色差量化步长表）

2.3 编码

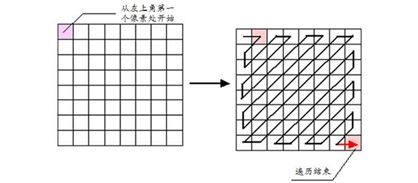
  DCT最后处理的步骤是熵编码，目的是在统计特征基础上通过对量化DCT系数进一步压缩，得到额外的无损压缩。根据信息论的原理，可以找到最佳数据压缩编码的方法，数据压缩的理论极限是信息熵。如果在编码过程中不损失信息量，即要求保持信息熵，则这种编码叫做熵编码。在编码之前，需要把二维变换的变换系数矩阵转换为一维序列。这样做的目的是为后续的熵编码做准备，即“之字形扫描”(如图3)。熵编码将之字形量化系数序列转换成中间符号序列，然后将这些符号转换成没有外部确定边界的数据流，即为最终编码后的图像数据流文件。

图3：Z字形排列方案   JPEG的基本系统的熵编码采纳了平均压缩比最高的编码哈夫曼编码，其理论依据是变字长编码理论。在变字长编码中，编码器的编码输出码字是长度不等的码字，按照编码输入信息符号出现的统计概率，给输出码字分配不同的字长，出现概率极高的分配较短的码字，反之出现概率较低的则分配较长的码字，从而得到较好的压缩效果。

3 MATLAB 仿真过程与结果

  根据 JPEG 压缩编码算法 , 对一幅图像进行JPEG 编 、解码的Matlab程序流程图, 如图 4 所示

图4：图像编、解码流程图   我们对Lnea图像进行仿真分析，图5（左中）是整幅图像经过DCT变换的频域分布图，图5（右）是分成8x8像素块做DCT变换的频域图像分布图。

图5 频域图像，其中左中整幅图像经过DCT变换的频域分布图，右图为成 像素块DCT变换的频域图像分布图   图6是 Lena 的原始图像和经过JPEG 压缩、重建后得到的图像，对比压缩前后的图像可知，压缩后的图像稍显模糊，这是因为该压缩算法为有损压缩，压缩后的图像丢失了原始图像部分数据信息，但由于DCT变换有使图像能量集中在左上方的特性，因此压缩图像保留了原始图像大部分的图像特征，其视觉效果与原始图像相差不大。

图6 原始图像和压缩后的图像

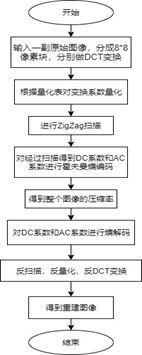
4. 结论

  本文首先介绍了JPEG压缩编码、解压算法接着使用MATLAB编程实现了JPEG图像压缩算法，对多幅标准灰度图像进行实验仿真，并对实验数据进行分析。实验结果表明，JPEG压缩算法实现简单，在很大的压缩范围内，都能得到很好的重建图像质量。正是由于具有这些优点，JPEG压缩编码算法在图像压缩领域得到了越来越广泛的应用。

参考文献：
[1] 吴术路. 基于DCT的JPEG图像压缩及实现[J]. 青海师范大学学报(自然科学版), 2010(03):41-43.
[2] 马媛媛, 杨峰, 信科,等. 基于DCT的JPEG图像压缩的研究[J]. 计算机技术与发展, 2011, 021(008):133-136.
[3] 方敏. JPEG算法的研究与实现[D]. 辽宁工程技术大学.
[4] 朱孔亮. 基于MATLAB的JPEG压缩编码[J]. 科技咨询导报, 2007(29):4-7.
[5] 吴桂军. 分层矢量量化DCT图象压缩算法设计与实现[D]. 四川大学, 2005.
[6] 赵文俊, 董慧敏, 朱智民. 基于Matlab的JPEG图像压缩编码仿真实现[J]. 机电工程, 2007(10):100-101+112.
[7] 李世军, 李鑫, 黄锋,等.图像压缩编码算法的仿真实现[J]. 湖南工程学院学报(自然科学版), 2009, 019(002):35-37.
[8] 陈斯斯, 王耀南, 王磊,等. 基于DSP的JPEG图像压缩编码的实现[J]. 计算机测量与控制, 2008(10):131-134.