Educational Codeforces Round 108 (Rated for Div. 2)A,B,C,D
Educational Codeforces Round 108 (Rated for Div. 2)
唠嗑:好好补题,整理博客,let‘s go!
A. Red and Blue Beans
题目链接.
题意:
输入t组数据,每组测试案例有三个数,第一个数表示red的数目和第二个数表示blue的数目。
1.把这些分成多组,确保每组至少有一个red或者blue。
2.red和blue的差值不能超过第三个数,问能否符合要求地分完。
题解:
比较简单的贪心,取出red和blue中较小的值,这个值就是我们要分的组数,如果较大的可以平均分给每组后差值不超过第三个数,则符合条件,不然不符合。
代码:
#include
#define endl '\n'
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N = 1e5+10,M=20;
const int inf=0x3f3f3f3f;
int n,m,t,x;
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>t;
while(t--){
cin>>n>>m>>x;
int mi = min(n, m);
int ma = max(n, m);
int ans = 0;
if(ma%mi){
ans++;
}
ans += ma / mi;
if(ans-1>x)
cout << "NO" << endl;
else
cout << "YES" << endl;
}
//system("pause");
return 0;
}
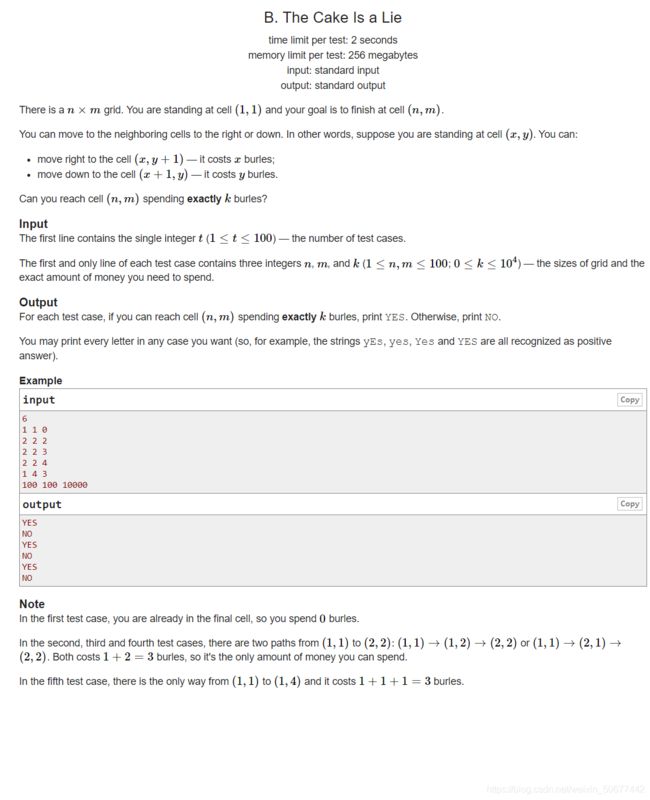
B. The Cake Is a Lie
直接上图:
题意:
给定t组数据,每组测试案例有三个数,分别表示目标位置的x和y,还有消耗的步数,计算规则是只能向下或者向右,向右步数算x,向下步数算y。
题解:
这题应该是要证明的,题目好像是用dp,但是我不会。。。(bushi)
通过枚举结果之后发现了规律:从(1,1)到每个位置不管路线怎么样,消耗的步数都是固定的。这样就很容易了。
代码:
#include
#define endl '\n'
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N = 1e5+10,M=20;
const int inf=0x3f3f3f3f;
int n,m,t,x;
int main(){
ios::sync_with_stdio(1),cin.tie(0),cout.tie(0);
cin>>t;
while(t--){
cin>>n>>m>>x;
if((n-1)+n*(m-1)==x)cout<<"YES"<<endl;
else
cout<<"NO"<<endl;
}
//system("pause");
return 0;
}
C. Berland Regional
题目链接.
题意:
题目给定t组测试案例,每组案例给定n名学生,这些学生有两个属性,归属的学校和能力值(输入给定),要求在每个学校选择1~n个学生参加后可以获得的最大的能力值之和。
题解:
这是一道排序加贪心的题目,各个学校分别从大到小排序,再取出符合条件的加入答案,注意使用前缀和维护。
代码:
#include
#define endl '\n'
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N = 2e5+10,M=20;
const int inf=0x3f3f3f3f;
int n,m,t,x;
int arr[N];
ll ans[N];
ll pre[N];
vector<int> vec[N];
bool cmp(int &a,int &b){
return a > b;
}
void solves(){
cin >> n;
for (int i = 1; i <= n;i++){
vec[i].clear();
ans[i] = 0;
pre[i] = 0;
}
for (int i = 1; i <= n;i++){
cin >> arr[i];
}
for (int i = 1; i <= n;i++){
cin >> x;
vec[arr[i]].push_back(x);
}
for (int i = 1; i <= n;i++){
int si = vec[i].size();
if(si==0)
continue;
sort(vec[i].begin(), vec[i].end(), cmp);
pre[0] = 0;
for (int j = 1; j <= si;j++){
pre[j] = pre[j - 1] + vec[i][j - 1];
}
for (int j = 1; j <= si;j++){
int cur = si / j * j;
ans[j] += pre[cur];
}
}
for (int i = 1; i <= n;i++){
cout << ans[i] << ' ';
} cout << endl;
}
int main(){
//ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>t;
while(t--){
solves();
}
system("pause");
return 0;
}
D. Maximum Sum of Products
题目链接
直接上图:
题意:
题目给定两个数组a,b,我们可以随便翻转其中某个子数组,使得a[i]*b[i]的值的和最大。
题解:
区间dp问题变形。
代码:
#include
#define endl '\n'
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N = 5e3+10,M=20;
const int inf=0x3f3f3f3f;
int n,m,t,x;
ll a[N], b[N];
ll l[N], r[N];
ll ans;
ll dp[N][N];
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin >> n;
for (int i = 1; i <= n;i++)
cin >> a[i];
for (int i = 1; i <= n;i++)
cin >> b[i];
for (int i = 1; i <= n;i++)
l[i] = l[i - 1] + a[i] * b[i];
for (int i = n; i >=1;i--)
r[i] = r[i + 1] + a[i] * b[i];
for (int i = 1; i <= n;i++)
dp[i][i] = a[i] * b[i];
for (int i = 1; i <= n-1;i++)
dp[i][i + 1] = a[i] * b[i + 1] + b[i] * a[i + 1];
for (int len = 3; len <= n;len++){
for (int i = 1; i <= n - len + 1;i++){
int j = i + len - 1;
dp[i][j] = dp[i + 1][j - 1] + a[i] * b[j] + b[i] * a[j];
}
}
for (int i = 1; i <= n;i++){
for (int j = i; j <= n;j++){
ans = max(ans, dp[i][j] + l[i - 1] + r[j + 1]);
}
}
cout << ans << endl;
//system("pause");
return 0;
}