神经网络可视化:Grad-CAM

论文题目：《Grad-CAM:Visual Explanations from Deep Networks via Gradient-based Localization》

作者单位：Georgia Institute of Technology，Facebook AI Research

年份：2017

公众号: CVpython 同步发布

导语：前段时间，用Grad-CAM来对神经网络的输出进行可视化，当时做的是一个多便签分类任务，但是可视化出来的结果感觉都点怪怪的，总感觉哪里不对。这次论文的总结让我对Gradm-CAM有了进一步的理解，终于知道当时可视化问题究竟在哪了，Oh yeah!。

1.论文要解决什么问题？

虽然CNN模型在CV领域取得了很大的突破，但是CNN就像一个“黑盒子一样”，里面究竟是怎么一回事，还是很难让人明白，可解释性很差。如果模型不work，其实也很难解析清楚究竟是为什么。所以作者提出Grad-CAM模型，对CNN所做的决策作出可视化解释。

2. 论文所提模型如何解决问题？

很多研究都表明CNN更深的层能够捕获更高级的视觉结构信息，而且，卷积特征中空间信息会在全连接层丢失，所以在最后卷积层，我们在高级的语义信息和详细的空间信息之间能够得到最好的折衷(为什么说这是一个折衷？)。Grad-CAM利用“流进”CNN的最后一层的梯度信息来理解每个神经元对决策的重要程度。

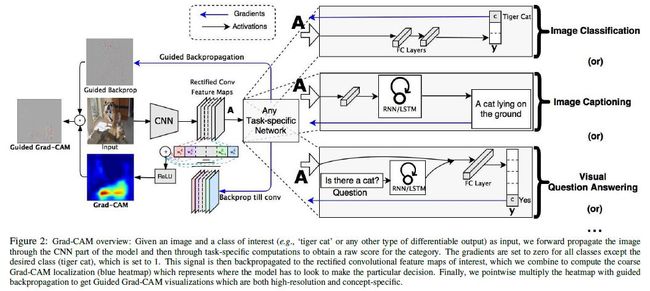
Grad-CAM总体结构如下图所示：

输入图像经过前向计算得到了特征映射$A$，对于类别$c$，在softmax之前有类别分数$y^c$。现在假设$A_{(x,y)}^k$为特征映射$A$在$(x,y)$位置的第$k$个通道的值，然后计算：

我们先来理解一下$y^c$对$A_{(x,y)}^k$的求导能够得到什么。

先举个简单的例子，对于公式$y=w1\ast x1+w2\ast x2$，其中$x1,x2$为自变量，$w1,w2$分别是两个自变量的系数，$y$对$x1$求偏导结果为$w1$，如果$x1$对$y$更加重要，$w1$系数自然也更大，所以$y$对$x1$的偏导结果也就更大了，那是不是说明了求导可以反映出自变量对函数的重要程度？答案是显然的(如果有大佬觉得不严谨，请指点)。

所以$y^c$对$A_{(x,y)}^k$的求导能够得到什么？得到的就是$A_{(x,y)}^k$这个特征值对$y^c$的重要程度，再来一个全局平均池化，得到就是特征映射第$k$个通道对$y^c$的重要程度了。

上面公式(1)求出了特征映射每个通道的系数，然后线性组合一下，如公式(2)所示。

加上$ReLU$的原因是因为作者只对那些对类别分数有正向影响的特征感兴趣，所以过滤了一下那些有负面影响的特征。

虽然Grad-CAM的可视化是具有类别判别力的，并且能够定位到相关的区域，但是它缺少显示细粒度重要性的能力。例如图1©，虽然Grad-CAM可以定位到猫的区域，但是为什么网络将它预测为“tiger cat”，从低分辨率的heat-map很难得到结论。为了能够定位的同时也显示细粒度，作者通过点乘将Guided Backpropagation 和Grad-CAM相结合，得到Guided Grad-CAM。如图1(d,j)所示。

3. 实验结果如何？

定位能力更好，分类也不弱。

4.对我们有什么指导意义？

感觉这才是最重要的点。

• Grad-CAM的可视化结果(包括区域和细粒度)为我们提供一个模型不work的解释，譬如某个图像分类错了，我们可视化一下，是感兴趣的区域有问题还是提取的细粒度特征有问题？
• 还可以验证数据集偏差，论文中有一个例子，例如识别医生和护士，可视化的结果显示模型定位的区域在人脸和发型，模型把有一些女医生识别成护士，而男护士识别成医生，存在性别偏见，以为男的就是医生，女的就是护士，看看数据集，会发现可能是因为78%的医生里面都是男的，而93%的护士都是女的，就存在数据集偏差。

本文由博客群发一文多发等运营工具平台 OpenWrite 发布