朴素贝叶斯-可靠性曲线-朴素贝叶斯和SVC预测概率的效果各方面都不如逻辑回归

``如果贝叶斯的模型效果不如其他模型，而我们又不想更换模型，那怎么办呢？如果以精确度
为指标来调整参数，贝叶斯估计是无法拯救了——不同于SVC和逻辑回归，贝叶斯的原理简单，根本没有什么可用的
参数。但是产出概率的算法有自己的调节方式，就是调节概率的校准程度。校准程度越高，模型对概率的预测越准
确，算法在做判断时就越有自信，模型就会更稳定。如果我们追求模型在概率预测上必须尽量贴近真实概率，那我们
就可以使用可靠性曲线来调节概率的校准程度`

#可靠性曲线
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification as mc#制作自己数据集的类
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression as LR
from sklearn.metrics import brier_score_loss
from sklearn.model_selection import train_test_split

#创建数据集
X,y=mc(n_samples=100000,n_features=20#总共20个特征
      ,n_classes=2#标签是2分类
      ,n_informative=2#其中两个代表较多信息
      ,n_redundant=10#10个都是冗余特征
      ,random_state=42)

#样本量足够大，因此使用1%的样本作为训练集，因为之前我们都知道
#朴素贝叶斯，即使是使用非常少的训练集，效果也会不错
Xtrain,Xtest,ytrain,ytest=train_test_split(X,y,test_size=0.99,random_state=42)

gnb=GaussianNB()
gnb.fit(Xtrain,ytrain)
y_pred=gnb.predict(Xtest)

prob_pos=gnb.predict_proba(Xtest)[:,1]
#利用字典来创建DATAFRAME
df=pd.DataFrame({"ytrue":ytest[:500],"probability":prob_pos[:500]})
df=df.sort_values(by="probability")
#索引变乱了
df.index=range(df.shape[0])```

fig=plt.figure()#画布
ax1=plt.subplot()#建立一个子图
ax1.plot([0,1],[0,1],"k:",label="perfectly calibrated")#
#画出对角线，X轴取值0-1，y轴取值0-1
#因为如果x=y,预测值和真实值越接近，那么曲线就越靠近对角线
#ax1.plot(df["probability"],df["ytrue"],"s-",label="%s(%1.3f)"%("bayes",clf_score))
ax1.plot(df["probability"],df["ytrue"],"s-")
ax1.set_ylabel("true label")
ax1.set_xlabel("predicted probability")
ax1.set_ylim([-0.05,1.05])
ax1.legend()
plt.show()

fig=plt.figure()#画布
ax1=plt.subplot()#建立一个子图
ax1.plot([0,1],[0,1],"k:",label="perfectly calibrated")#
#画出对角线，X轴取值0-1，y轴取值0-1
#因为如果x=y,预测值和真实值越接近，那么曲线就越靠近对角线
#ax1.plot(df["probability"],df["ytrue"],"s-",label="%s(%1.3f)"%("bayes",clf_score))
ax1.scatter(df["probability"],df["ytrue"],s=10)
ax1.set_ylabel("true label")
ax1.set_xlabel("predicted probability")
ax1.set_ylim([-0.05,1.05])
ax1.legend()
plt.show()

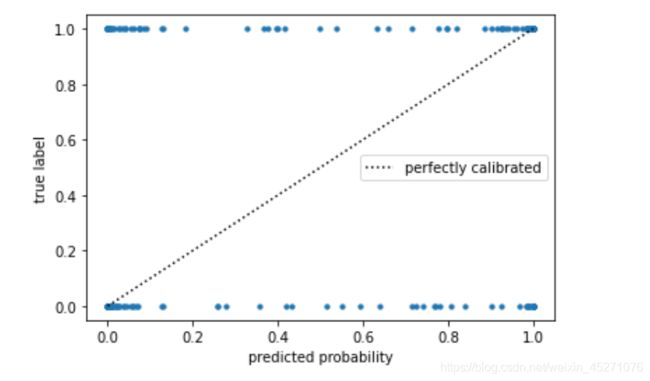
可以看到，由于真实标签是0和1，所以所有的点都在y=1和y=0这两条直线上分布，这完全不是我们希望看到的图
像。回想一下我们的可靠性曲线的横纵坐标：横坐标是预测概率，而纵坐标是真实值，我们希望预测概率很靠近真实
值，那我们的真实取值必然也需要是一个概率才可以，如果使用真实标签，那我们绘制出来的图像完全是没有意义
的。但是，我们去哪里寻找真实值的概率呢？这是不可能找到的——如果我们能够找到真实的概率，那我们何必还用
算法来估计概率呢，直接去获取真实的概率不就好了么？所以真实概率在现实中是不可获得的。但是，我们可以获得
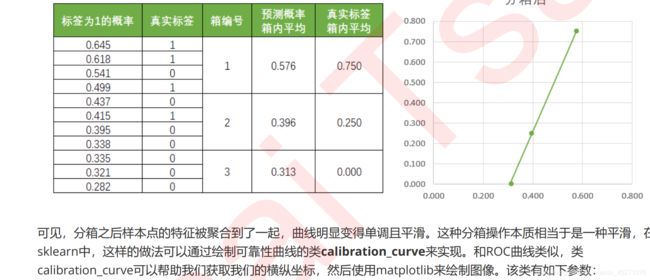
类概率的指标来帮助我们进行校准。一个简单的做法是，将数据进行分箱，然后规定每个箱子中真实的少数类所占的
比例为这个箱上的真实概率trueproba，这个箱子中预测概率的均值为这个箱子的预测概率predproba，然后以
trueproba为纵坐标，predproba为横坐标，来绘制我们的可靠性曲线

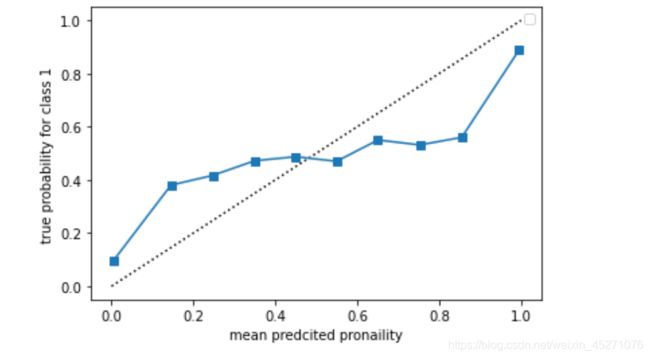
#因为真实概率不可能找到，不过我们可以找到类概率
from sklearn.calibration import calibration_curve
trueprob,preproba=calibration_curve(ytest,prob_pos,n_bins=10)
fig=plt.figure()
ax1=plt.subplot()
ax1.plot([0,1],[0,1],"k:")
ax1.plot(preproba,trueprob,"s-")
ax1.set_ylabel("true probability for class 1")
ax1.set_ylabel("mean predcited pronaility")
ax1.set_ylim([-0.05,1.05])
ax1.legend()
plt.show()

调用enumerate函数。调用enumerate函数的写法是：enumerate(序列)。作用是为序列中的元素加上序号。生成的结果也是一个序列。

举一个例子说明enumerate函数的用法。enumerate([‘a’, ‘b’, ‘c’])的值是：[(0, ‘a’), '(1, ‘b’), (2, ‘c’)]。(0, ‘a’)有两项，第一项是序号，第二项是原列表的元素。

再举一个例子说明enumerate函数的用法。enumerate([1.5, 2.8, 3.14, 5.6])的值是：[(0, 1.5), (1, 2.8), (3, 3.14), (4, 5.6)]。(0, 1.5)有两项，第一项是序号，第二项是原列表的元素。(4, 5.6)也一样，第一项是序号，第二项是原列表的元素。
ig,ax = plt.subplots()

使用该函数确定图的位置，掉用时要XXX=ax.(ax是位置）

等价于：

fig = plt.figure()
ax = fig.add_subplot(1,1,1)
fig 是图像对象，ax 是坐标轴对象
fig, ax = plt.subplots(1,3),其中参数1和3分别代表子图的行数和列数，一共有 1x3 个子图像。函数返回一个figure图像和子图ax的array列表。

fig, ax = plt.subplots(1,3,1),最后一个参数1代表第一个子图。
如果想要设置子图的宽度和高度可以在函数内加入figsize值

#不同得分箱下曲线是如何变化得
fig=plt.figure()
axes=plt.subplots(1,3,figsize=(18,4))
#fig,axes=plt.subplots(1,3,figsize=(18,4))

fig,axes=plt.subplots(1,3,figsize=(18,4))
for ind ,i in enumerate([3,10,100]):
    ax=axes[ind]
    trueprob,preproba=calibration_curve(ytest,prob_pos,n_bins=i)
    ax.plot([0,1],[0,1],"k:")
    ax.plot(preproba,trueprob,"s-")
    ax.set_ylabel("true probability for class 1")
    ax.set_xlabel("mean predcited pronaility")
    ax.set_ylim([-0.05,1.05])
    ax.legend()
plt.show()

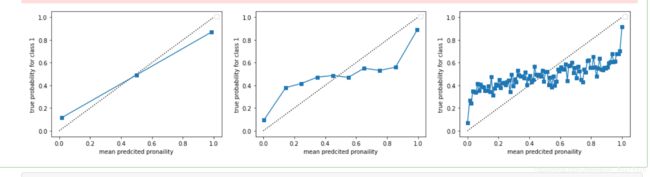
很明显可以看出，n_bins越大，箱子越多，概率校准曲线就越精确，但是太过精确的曲线不够平滑，无法和我们希望
的完美概率密度曲线相比较。n_bins越小，箱子越少，概率校准曲线就越粗糙，虽然靠近完美概率密度曲线，但是无
法真实地展现模型概率预测地结果。因此我们需要取一个既不是太大，也不是太小的箱子个数，让概率校准曲线既不
是太精确，也不是太粗糙，而是一条相对平滑，又可以反应出模型对概率预测的趋势的曲线。通常来说，建议先试试
看箱子数等于10的情况。箱子的数目越大，所需要的样本量也越多，否则曲线就会太过精确

#建立循环，绘制多个模型得概率密度曲线
name=["GaussianBayes","Logistic","SVC"]
gnb=GaussianNB()
logi=LR(C=1.,solver='lbfgs',max_iter=3000,multi_class="auto")
#优化算法选择参数：solver,lbfgs：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
#分类方式选择参数：multi_class
#C是用来控制正则化程度的超参数,C正则化强度的倒数，必须是一个大于0的浮点数，不填写默认1.0，
#即默认正则项与损失函数的比值是1：1。
#C越小，损失函数会越小，模型对损失函数的惩罚越重，正则化的效力越强，参数会逐渐被压缩得越来越小
svc=SVC(kernel="linear",gamma=1.)
fig,ax1=plt.subplots(figsize=(8,6))
ax1.plot([0,1],[0,1],"k:")#画出对角线
for clf,name_ in zip([gnb,logi,svc],name):
    clf.fit(Xtrain,ytrain)
    y_pred=clf.predict(Xtest)
    if hasattr(clf,"predict_proba"):
        prob_pos=clf.predict_proba(Xtest)[:,1]
    else :
        prob_pos=clf.decision_function(Xtest)
        prob_pos=(prob_pos-prob_pos.min())/(prob_pos.max()-prob_pos.min())
    clf_score=brier_score_loss(ytest,prob_pos,pos_label=y.max())
    trueprob,preproba=calibration_curve(ytest,prob_pos,n_bins=10)
    ax1.plot(preproba,trueprob,"s-",label="%s(%1.3f)"%(name_,clf_score))
    ax1.set_ylabel("true probability for class 1")
    ax1.set_xlabel("mean predcited pronaility")
    ax1.set_ylim([-0.05,1.05])
    ax1.legend()
plt.show()

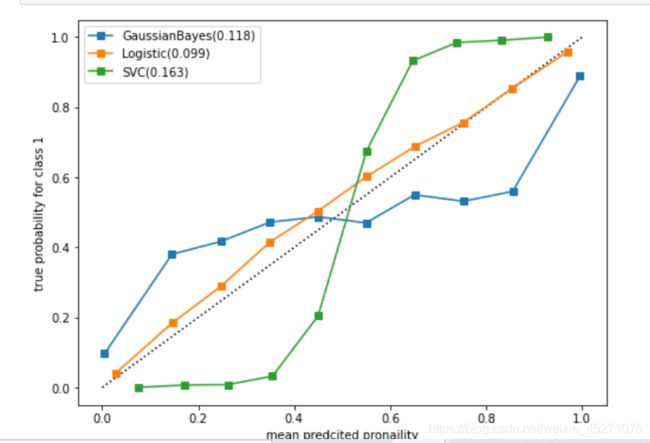
从图像的结果来看，我们可以明显看出，逻辑回归的概率估计是最接近完美的概率校准曲线，所以逻辑虎归的效果最
完美。相对的，高斯朴素贝叶斯和支持向量机分类器的结果都比较糟糕。支持向量机呈现类似于sigmoid函数的形
状，而高斯朴素贝叶斯呈现和Sigmoid函数相反的形状。
对于贝叶斯，如果概率校准曲线呈现sigmoid函数的镜像的情况，则说明数据集中的特征不是相互条件独立的。贝叶
斯原理中的”朴素“原则：特征相互条件独立原则被违反了（这其实是我们自己的设定，我们设定了10个冗余特征，这
些特征就是噪音，他们之间不可能完全独立），因此贝叶斯的表现不够好。
而支持向量机的概率校准曲线效果其实是典型的置信度不足的分类器(under-confident classifier)的表现：大量的样
本点集中在决策边界的附近，因此许多样本点的置信度靠近0.5左右，即便决策边界能够将样本点判断正确，模型本
身对这个结果也不是非常确信的。相对的，离决策边界很远的点的置信度就会很高，因为它很大可能性上不会被判断
错误。支持向量机在面对混合度较高的数据的时候，有着天生的置信度不足的缺点

我们可以通过绘制直方图来查看模型的预测概率的分布。直方图是以样本的预测概率分箱后的结果为横坐标，每个箱
中的样本数量为纵坐标的一个图像。注意，这里的分箱和我们在可靠性曲线中的分箱不同，这里的分箱是将预测概率
均匀分为一个个的区间，与之前可靠性曲线中为了平滑的分箱完全是两码事。我们来绘制一下我们的直方图

name=["GaussianBayes","Logistic","SVC"]
gnb=GaussianNB()
logi=LR(C=1.,solver='lbfgs',max_iter=3000,multi_class="auto")
#优化算法选择参数：solver,lbfgs：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
#分类方式选择参数：multi_class
#C是用来控制正则化程度的超参数,C正则化强度的倒数，必须是一个大于0的浮点数，不填写默认1.0，
#即默认正则项与损失函数的比值是1：1。
#C越小，损失函数会越小，模型对损失函数的惩罚越重，正则化的效力越强，参数会逐渐被压缩得越来越小
svc=SVC(kernel="linear",gamma=1.)
fig,ax2=plt.subplots(figsize=(8,6))
for clf,name_ in zip([gnb,logi,svc],name):
    clf.fit(Xtrain,ytrain)
    y_pred=clf.predict(Xtest)
    if hasattr(clf,"predict_proba"):#hasattr(obj,name)：查看一个类obj中是否存在名字为name的接口，存在则返回True
        prob_pos=clf.predict_proba(Xtest)[:,1]
    else :
        prob_pos=clf.decision_function(Xtest)
        prob_pos=(prob_pos-prob_pos.min())/(prob_pos.max()-prob_pos.min())
    ax2.hist(prob_pos#只设置横坐标即可，纵坐标是该概率下样本的数量
        ,bins=10
        ,label=name_
         ,histtype="step" #设置直方图为透明
         ,lw=2 #设置直方图每个柱子描边的粗细
                )
ax2.set_ylabel("Distribution of probability")
ax2.set_xlabel("Mean predicted probability")
ax2.set_xlim([-0.05, 1.05])
ax2.set_xticks([0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1])
ax2.legend(loc=9)
plt.show()

可以看到，高斯贝叶斯的概率分布是两边非常高，中间非常低，几乎90%以上的样本都在0和1的附近，可以说是置信
度最高的算法，但是贝叶斯的布里尔分数却不如逻辑回归，这证明贝叶斯中在0和1附近的样本中有一部分是被分错
的。支持向量贝叶斯完全相反，明显是中间高，两边低，类似于正态分布的状况，证明了我们刚才所说的，大部分样
本都在决策边界附近，置信度都徘徊在0.5左右的情况。而逻辑回归位于高斯朴素贝叶斯和支持向量机的中间，即没
有太多的样本过度靠近0和1，也没有形成像支持向量机那样的正态分布。一个比较健康的正样本的概率分布，就是逻
辑回归的直方图显示出来的样子
大家也许还记得我们说过，我们是假设样本的概率分布为高斯分布，然后使用高斯的方程来估计连续型变量的概
率。怎么现在我们绘制出的概率分布结果中，高斯普斯贝叶斯的概率分布反而完全不是高斯分布了呢？
注意，千万不要把概率密度曲线和概率分布直方图混淆。
在称重汉堡的时候所绘制的曲线，是概率密度曲线，横坐标是样本的取值，纵坐标是落在这个样本取值区间中的
样本个数，衡量的是每个X的取值区间之内有多少样本。服从高斯分布的是X的取值上的样本分布。
现在我们的概率分布直方图，横坐标是概率的取值[0,1]，纵坐标是落在这个概率取值范围中的样本的个数，衡
量的是每个概率取值区间之内有多少样本。这个分布，是没有任何假设的

#包装函数
def plot_calib(models,name,Xtrain,Xtest,ytrain,ytest,n_bins=10):
    import matplotlib.pyplot as plt
    from sklearn.metrics import brier_score_loss
    from sklearn.calibration import calibration_curve
    fig,(ax1,ax2)=plt.subplots(1,2,figsize=(30,10))
    ax1.plot([0,1],[0,1],"k:",label="Perfectly calibrated")
    for clf,name_ in zip(models,name):
        clf.fit(Xtrain,ytrain)
        y_pred=clf.predict(Xtest)
        if hasattr(clf,"predict_proba"):#hasattr(obj,name)：查看一个类obj中是否存在名字为name的接口，存在则返回True
            prob_pos=clf.predict_proba(Xtest)[:,1]
        else :
            prob_pos=clf.decision_function(Xtest)
            prob_pos=(prob_pos-prob_pos.min())/(prob_pos.max()-prob_pos.min())
        clf_score=brier_score_loss(ytest,prob_pos,pos_label=y.max())
        trueprob,preproba=calibration_curve(ytest,prob_pos,n_bins=n_bins)
        ax1.plot(preproba,trueprob,"s-",label="%s(%1.3f)"%(name_,clf_score))
        ax2.hist(prob_pos#只设置横坐标即可，纵坐标是该概率下样本的数量
                 ,range=(0,1)
                 ,bins=n_bins
                 ,label=name_
                 ,histtype="step" #设置直方图为透明
                 ,lw=2 #设置直方图每个柱子描边的粗细
                )
ax2.set_ylabel("Distribution of probability")
ax2.set_xlabel("Mean predicted probability")
ax2.set_xlim([-0.05, 1.05])
ax2.set_xticks([0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1])
ax2.legend(loc=9)
ax2.set_title("Distribution of probablity")
ax1.set_ylabel("true probability for class 1")
ax1.set_xlabel("mean predcited pronaility")
ax1.set_ylim([-0.05,1.05])
ax1.legend()
ax1.set_title("Calibration plots(reliabilty curve)")
plt.show()

from sklearn.calibration import CalibratedClassifierCV
name=["GaussianBayes","Logistic","Bayes+isotonic","Bayes+sigmoid"]
gnb=GaussianNB()
logi=LR(C=1.,solver='lbfgs',max_iter=3000,multi_class="auto")
models=[gnb,logi,CalibratedClassifierCV(gnb,method="isotonic"),CalibratedClassifierCV(gnb,method="sigmoid")]

plot_calib(models,name,Xtrain,Xtest,ytrain,ytest)

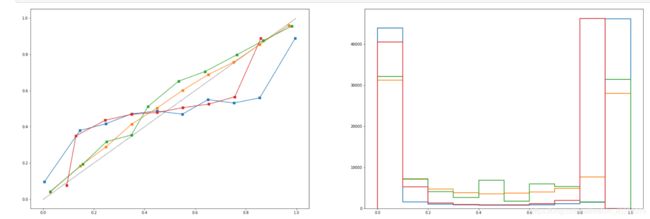
从校正朴素贝叶斯的结果来看，Isotonic等渗校正大大改善了曲线的形状，几乎让贝叶斯的效果与逻辑回归持平，并
且布里尔分数也下降到了0.098，比逻辑回归还低一个点。Sigmoid校准的方式也对曲线进行了稍稍的改善，不过效
果不明显。从直方图来看，Isotonic校正让高斯朴素贝叶斯的效果接近逻辑回归，而Sigmoid校正后的结果依然和原
本的高斯朴素贝叶斯更相近。可见，当数据的特征之间不是相互条件独立的时候，使用Isotonic方式来校准概率曲
线，可以得到不错的结果，让模型在预测上更加谦虚。

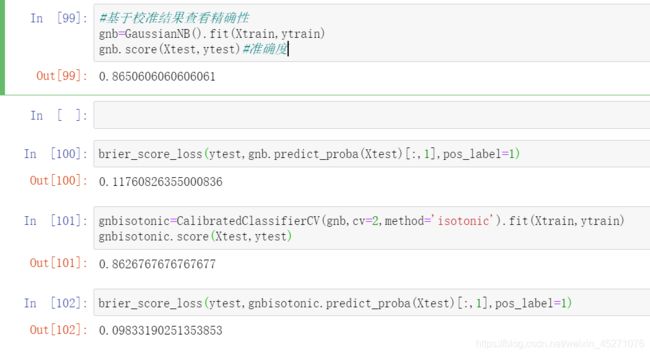
可以看出，校准概率后，布里尔分数明显变小了，但整体的准确率却略有下降，这证明算法在校准之后，尽管对概率
的预测更准确了，但模型的判断力略有降低。来思考一下：布里尔分数衡量模型概率预测的准确率，布里尔分数越
低，代表模型的概率越接近真实概率，**当进行概率校准后，本来标签是1的样本的概率应该会更接近1，而标签本来是
0的样本应该会更接近0，没有理由布里尔分数提升了，模型的判断准确率居然下降了。但从我们的结果来看，模型的
准确率和概率预测的正确性并不是完全一致的，为什么会这样呢？
对于不同的概率类模型，原因是不同的。对于SVC，决策树这样的模型来说，概率不是真正的概率，而更偏向于是一
个“置信度”，这些模型也不是依赖于概率预测来进行分类（决策树依赖于树杈而SVC依赖于决策边界），因此对于这
些模型，可能存在着类别1下的概率为0.4但样本依然被分类为1的情况，这种情况代表着——模型很没有信心认为这
个样本是1，但是还是坚持把这个样本的标签分类为1了。这种时候，概率校准可能会向着更加错误的方向调整（比如
把概率为0.4的点调节得更接近0，导致模型最终判断错误），因此出现布里尔分数可能会显示和精确性相反的趋势。
而对于朴素贝叶斯这样的模型，却是另一种情况。注意在朴素贝叶斯中，我们有各种各样的假设，除了我们的“朴
素”假设，还有我们对概率分布的假设（比如说高斯），这些假设使得我们的贝叶斯得出的概率估计其实是有偏估
计，也就是说，这种概率估计其实不是那么准确和严肃。我们通过校准，让模型的预测概率更贴近于真实概率，本质
是在统计学上让算法更加贴近我们对整体样本状况的估计，这样的一种校准在一组数据集上可能表现出让准确率上
升，也可能表现出让准确率下降，这取决于我们的测试集有多贴近我们估计的真实样本的面貌。这一系列有偏估计使
得我们在概率校准中可能出现布里尔分数和准确度的趋势相反的情况。
当然，可能还有更多更深层的原因，比如概率校准过程中的数学细节如何影响了我们的校准，类calibration_curve中
是如何分箱，如何通过真实标签和预测值来生成校准曲线使用的横纵坐标的，这些过程中也可能有着让布里尔分数和
准确率向两个方向移动的过程。
在现实中，当两者相悖的时候，请务必以准确率为标准。但是这不代表说布里尔分数和概率校准曲线就无效了。概率
类模型几乎没有参数可以调整，除了换模型之外，鲜有更好的方式帮助我们提升模型的表现，概率校准是难得的可以
帮助我们针对概率提升模型的方法

#对SVC进行校准
from sklearn.calibration import CalibratedClassifierCV
svcname=["SVC","Logistic","SVC+isotonic","SVC+sigmoid"]
svc=SVC(kernel="linear",gamma=1)
logi=LR(C=1.,solver='lbfgs',max_iter=3000,multi_class="auto")
models=[svc,logi,CalibratedClassifierCV(svc,method="isotonic"),CalibratedClassifierCV(svc,method="sigmoid")]

可以看出，对于SVC，sigmoid和isotonic的校准效果都非常不错，无论是从校准曲线来看还是从概率分布图来看，两
种校准都让SVC的结果接近逻辑回归，其中sigmoid更加有效。来看看不同的SVC下的精确度结果

name_svc=["SVC","SVC+isotonic","SVC+sigmoid"]
svc=SVC(kernel="linear",gamma=1)
models_svc=[svc,CalibratedClassifierCV(svc,cv=2,method="isotonic"),
           CalibratedClassifierCV(svc,cv=2,method="sigmoid")]
for clf,name in zip(models_svc,name_svc):
    clf.fit(Xtrain,ytrain)
    y_pred=clf.predict(Xtest)
    if hasattr(clf,"predict_proba"):
        prob_pos=clf.predict_proba(Xtest)[:,1]
    else:
        prob_pos=clf.decision_function(Xtest)
        prob_pos=(prob_pos-prob_pos.min())/(prob_pos.max()-prob_pos.min())
    clf_score=brier_score_loss(ytest,prob_pos,pos_label=prob_pos.max())
    score=clf.score(Xtest,ytest)
    print("{}:".format(name))
    print("\tBrier:{:.4f}".format(clf_score))
    print("\tAccuracy:{:.4f}".format(score))

可以看到，对于SVC来说，两种校正都改善了准确率和布里尔分数。可见，概率校正对于SVC非常有效。这也说明，
概率校正对于原本的可靠性曲线是形容Sigmoid形状的曲线的算法比较有效。
在现实中，我们可以选择调节模型的方向，我们不一定要追求最高的准确率或者追求概率拟合最好，我们可以根据自
己的需求来调整模型。当然，对于概率类模型来说，由于可以调节的参数甚少，所以我们更倾向于追求概率拟合，并
使用概率校准的方式来调节模型。如果你的确希望追求更高的准确率和Recall，可以考虑使用天生就非常准确的概率
类模型逻辑回归，也可以考虑使用除了概率校准之外还有很多其他参数可调的支持向量机分类器