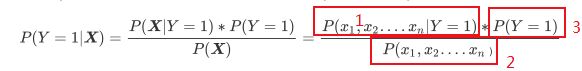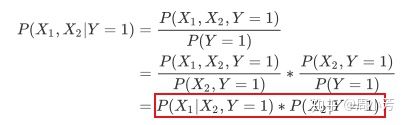手写数字数据集_机器学习4（朴素贝叶斯：高斯、多项式、伯努利，手写数据集案例）...

机器学习算法应用领域
支持向量机：图像识别、人脸识别
朴素贝叶斯：数字识别、文字识别、垃圾邮箱分类、传媒行业的文本挖掘

from PIL import Image 
import numpy as np

image = Image.open('QQ图片.png') #显示图片
image_arr = np.array(image)  #显示数组
image_arr.ravel() #将三维数组平铺成一维数组

高维稀疏矩阵：特征数量很多，但是是离散型的，离得很开，很稀疏

朴素贝叶斯擅长处理高维稀疏矩阵，不擅长处理连续的，比如数字识别/文字识别，朴素贝叶斯会有一个比较好的效果，应用领域包括：垃圾邮箱分类/传媒行业的文本挖掘

#高斯朴素贝叶斯---处理连续型变量，要求数据符合高斯分布（有一定能力处理样本不均衡问题）

# 导包
import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split

# 导数据集
数据集：1797个手写数字，每个样本是一个8 x 8的像素点，所以最终的数据是1797 x 64
digits = load_digits()
X, y = digits.data, digits.target

# 切分训练集和测试集
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size=0.3,random_state=420)

# 手写数字可视化
%matplotlib inline
from matplotlib import pyplot as plt
images_and_labels = list(zip(digits.images,digits.target))
plt.figure(figsize=(8,6),dpi=200)     #宽高,单位是inches, 分辨率
for index, (image,label) in enumerate(images_and_labels[:12]):
    plt.subplot(3,4,index+1)     #行数,列数(从1开始),第几张图(按行数)
    plt.axis("off")      #关闭坐标轴
    plt.imshow(image,cmap=plt.cm.gray_r,interpolation="nearest")  
    # cmap设置色图到灰色 interpolation 像素间颜色连接方法
    plt.title("Digit: %i" % label, fontsize=20)

# 利用sklearn实现朴素贝叶斯算法
gnb = GaussianNB().fit(Xtrain,Ytrain)
acc_score = gnb.score(Xtest,Ytest) #接口 查看分数
acc_score
Y_pred = gnb.predict(Xtest) #接口 查看预测结果
prob = gnb.predict_proba(Xtest) #接口 查看预测概率
prob.shape #每一列对应一个标签下的概率
prob[1,:].sum() #每一行的和都是一
prob.sum(axis=1)

from sklearn.metrics import confusion_matrix as CM #混淆矩阵
CM(Ytest,Y_pred)

#伯努利朴素贝叶斯----只能处理二项分布数据，擅长处理文本较短的数据集，文本挖掘。数据归一化之后预测效果变低，需设定阈值，对样本不均衡不敏感（哑变量/二项化/要符合二项分布的数据特点），但对数据的要求很高

from sklearn.naive_bayes import BernoulliNB

#普通来说我们应该使用二值化的类sklearn.preprocessing.Binarizer来将特征一个个二值化
#然而这样效率过低，因此我们选择归一化之后直接设置一个阈值

mms = MinMaxScaler().fit(Xtrain)
Xtrain_ = mms.transform(Xtrain)
Xtest_ = mms.transform(Xtest)
#不设置二值化
bnl_ = BernoulliNB().fit(Xtrain_, Ytrain)
bnl_.score(Xtest_,Ytest)
#设置二值化阈值为0.5
bnl = BernoulliNB(binarize=0.5).fit(Xtrain_, Ytrain)
bnl.score(Xtest_,Ytest)

#多项式朴素贝叶斯 -----处理离散型变量。它所涉及的特征往往是次数、频数、计数，sklearn中的多项式朴素贝叶斯不接受负值的输入,受数据结构非常大的影响

#导包
from sklearn.preprocessing import MinMaxScaler
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn.databases import make_blobs
#制定数据集
class_1 = 500 
class_2 = 500 #两个类别分别设定500个样本
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [0.5, 0.5] #设定两个类别的方差
X, y = make_blobs(n_samples=[class_1, class_2],
                  centers=centers,
                  cluster_std=clusters_std,
                  random_state=0, shuffle=False)

Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y
                                                ,test_size=0.3
                                                ,random_state=420)
#查看数据集
np.unique(Ytrain)
(Ytrain == 1).sum()/Ytrain.shape[0]

#先归一化，保证输入多项式朴素贝叶斯的特征矩阵中不带有负数
mms = MinMaxScaler().fit(Xtrain)
Xtrain_ = mms.transform(Xtrain)
Xtest_ = mms.transform(Xtest)
 
#利用sklearn实现伯努利朴素贝叶斯
mnb = MultinomialNB().fit(Xtrain_, Ytrain)

#重要属性：调用根据数据获取的，每个标签类的对数先验概率log(P(Y))
#由于概率永远是在[0,1]之间，因此对数先验概率返回的永远是负值
mnb.class_log_prior_ #接口 
mnb.class_log_prior_.shape
np.exp(mnb.class_log_prior_) #接口 可以使用np.exp来查看真正的概率值
mnb.feature_log_prob_ #重要接口 返回一个固定标签类别下的每个特征的对数概率log(P(Xi|y))
mnb.feature_log_prob_.shape 
mnb.class_count_  #重要接口 在fit时每个标签类别下包含的样本数
mnb.class_count_.shape #当fit接口中的sample_weight被设置时，该接口返回的值也会受到加权的影响
mnb.predict(Xtest_) #接口 预测值
mnb.predict_proba(Xtest_) #接口 预测概率
mnb.score(Xtest_,Ytest) #接口 得分

# 对比高斯朴素贝叶斯和其他算法（支持向量机、随机森林、决策树、逻辑回归）

# 导包
import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.tree import DecisionTreeClassifier as DTC
from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_digits
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit  #随机选取，随机抽样
from time import time
import datetime

# 定义学习曲线的函数
def plot_learning_curve(estimator,title, X, y,  #estimator设置迭代的模型
                        ax, #选择子图
                        ylim=None, #设置纵坐标的取值范围
                        cv=None, #交叉验证
                        n_jobs=None #设定索要使用的线程，对于大数据量，只要n_jobs设置的足够大，就可以充分调用CPU来跑
                       ):
    train_sizes, train_scores, test_scores = learning_curve(estimator, X, y
                                                            ,cv=cv,n_jobs=n_jobs)    
    ax.set_title(title)
    if ylim is not None:
        ax.set_ylim(*ylim)
    ax.set_xlabel("Training examples")
    ax.set_ylabel("Score")
    ax.grid() #显示网格作为背景，不是必须
    ax.plot(train_sizes, np.mean(train_scores, axis=1), 'o-'
            , color="r",label="Training score")
    ax.plot(train_sizes, np.mean(test_scores, axis=1), 'o-'
            , color="g",label="Test score")
    ax.legend(loc="best")
    return ax


# 绘制不同数据量下的高斯朴素贝叶斯的学习曲线
estimator = GaussianNB()
plt.figure()
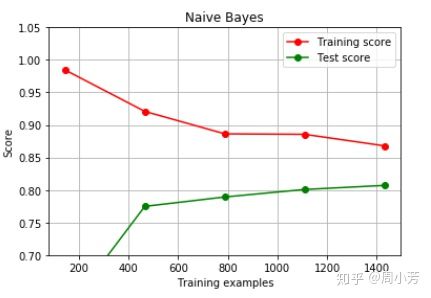
plot_learning_curve(estimator, "Naive Bayes", X, y,
                        ax=plt.gca(), ylim = [0.7, 1.05],n_jobs=4, cv=5); #plt.gca定义的是图片的样式

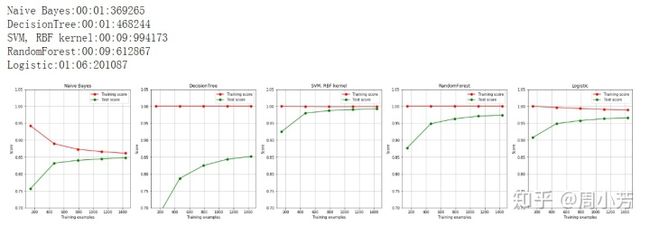
# 对比多种不同模型下的学习时间和模型效果
title = ["Naive Bayes","DecisionTree","SVM, RBF kernel","RandomForest","Logistic"] 
model = [GaussianNB(),DTC(),SVC(gamma=0.001)
         ,RFC(n_estimators=50),LR(C=.1,solver="saga")]

fig, axes = plt.subplots(1,5,figsize=(30,6))
for ind,title_,estimator in zip(range(len(title)),title,model):
    times = time()
    plot_learning_curve(estimator, title_, X, y,
                        ax=axes[ind], ylim = [0.7, 1.05],n_jobs=4, cv=cv)
    print("{}:{}".format(title_,datetime.datetime.fromtimestamp(time()-times).strftime("%M:%S:%f")))
plt.show()

当样本量越大，高斯朴素贝叶斯的运算效率越低

# 通过绘制高斯朴素贝叶斯的学习曲线与决策树，随机森林，和支持向量机的学习曲线做对比，探索高斯朴素贝叶斯算法在拟合上的性质

朴素贝叶斯运算最快，支持向量机的模型效果最好

观察运行时间：

• 跑的最快的是决策树，因为决策树有“偷懒”行为，它会选取特征重要性大的特征进行模型训练
• 其次是贝叶斯，贝叶斯是一个比较简单的算法，对于这种高维的数据来说，也比较快
• 对于一些复杂的算法，比如支持向量机、随机森林，用的时间就相对较长了。当然，对于支持向量机来说，高维的稀疏矩阵还可以，如果处理的是大数据，支持向量机会更慢一些。
• 逻辑回归属于线性回归的一种，为什么也会比较慢，因为逻辑回归对于线性数据来说准确性和速度都是比较高的，对于这种高维稀疏矩阵，逻辑回归是不太擅长的。

观察学习曲线：

朴素贝叶斯是中规中矩的、决策树明显出现过拟合、支持向量机、随机森林准确性都很高

# 对比不同朴素贝叶斯的学习效果和学习时长（高斯、多项式、伯努利、补集朴素贝叶斯）

#导包
from sklearn.naive_bayes import MultinomialNB, GaussianNB, BernoulliNB, ComplementNB
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_blobs
from sklearn.preprocessing import KBinsDiscretizer #分箱
from sklearn.metrics import recall_score,roc_auc_score as AUC
from time import time
import datetime
from sklearn.preprocessing import MinMaxScaler

#利用make_blobs制定数据集
class_1 = 50000 #多数类为50000个样本
class_2 = 500 #少数类为500个样本
centers = [[0.0, 0.0], [5.0, 5.0]] #设定两个类别的中心
clusters_std = [3, 1] #设定两个类别的方差
X, y = make_blobs(n_samples=[class_1, class_2],
                  centers=centers,
                  cluster_std=clusters_std,
                  random_state=0, shuffle=False)
X.shape

np.unique(y)

# 利用sklearn实现不用贝叶斯的算法
name = ["Multinomial","Gaussian","Bernoulli","Complement"]
models = [MultinomialNB(),GaussianNB(),BernoulliNB(),ComplementNB()]

for name,clf in zip(name,models):
    times = time()
    Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y
                                                ,test_size=0.3
                                                ,random_state=420)
    
    #归一化
    mms = MinMaxScaler().fit(Xtrain)
    Xtrain_ = mms.transform(Xtrain)
    Xtest_ = mms.transform(Xtest)

    #分箱
    if name != "Gaussian":
        kbs = KBinsDiscretizer(n_bins=10, encode='onehot').fit(Xtrain) 
        Xtrain = kbs.transform(Xtrain)
        Xtest = kbs.transform(Xtest)
    
      
    clf.fit(Xtrain,Ytrain)
    y_pred = clf.predict(Xtest)
    proba = clf.predict_proba(Xtest)[:,1]
    score = clf.score(Xtest,Ytest)
    print(name)
    print("tAccuracy:{:.3f}".format(score))  #输出精确度
    print("tRecall:{:.3f}".format(recall_score(Ytest,y_pred)))  #输出召回率
    print("tAUC:{:.3f}".format(AUC(Ytest,proba)))   # 输出AUC
    print(datetime.datetime.fromtimestamp(time()-times).strftime("%M:%S:%f")) #输出计算时间

补集朴素贝叶斯提高了捕捉少数类的能力

样本不均衡时，评估少数类样本的评估指标用召回率，0.4已经差不多

二、朴素贝叶斯的理解

目的是求：p(Y|X)

假设有两个特征，P（Y|X）的计算公式是：

1：可以根据下面公式求得（也可以直接求得~）

2：不能直接求，但可以根据下面公式求得（如果变量之间相互独立，那么p(x) = p(x1)*p(x2)）

3：可以直接求

三、朴素贝叶斯的计算案例

数据集

预测的问题是：在吃很多肉，锻炼天数为20天的情况下，是否会长胖？

目的是求：

1：

2.

3. p(长胖)=1/4

所以，最终的结果是：

所以，在吃很多肉并且运动20天的条件下，长胖的概率是1/3.