机器学习-动手学深度学习pytorch版1-3章笔记

这是动手学深度学习pytorch版学习笔记，其中每次笔记都对应几个章节。

1.深度学习简介

1.1 起源

雅各比·伯努利（1655–1705）：伯努利分布
卡尔·弗里德里希·高斯（1777–1855）：最小二乘法
罗纳德·费雪（1890–1962）：统计学理论
克劳德·香农（1916–2001）的信息论
阿兰·图灵 （1912–1954）的计算理论
唐纳德·赫布（1904–1985）：赫布理论
亚历山大·贝恩（1818–1903）和查尔斯·斯科特·谢灵顿（1857–1952）：神经网络
绝大多数神经网络都包含以下的核心原则：
1）交替使用线性处理单元与非线性处理单元，它们经常被称为“层”。
2）使用链式法则（即反向传播）来更新网络的参数。

1.2 发展

近十年来深度学习长足发展的部分原因：
1）优秀的容量控制方法，如丢弃法
2）注意力机制解决了另一个困扰统计学超过一个世纪的问题
3）记忆网络 [6]和神经编码器—解释器 [7]这样的多阶设计使得针对推理过程的迭代建模方法变得可能。
4）生成对抗网络的发明
5）分布式并行训练算法+GPU
6）并行计算的能力
7）深度学习框架也在传播深度学习思想的过程中扮演了重要角色。Caffe、 Torch和Theano。TensorFlow。

1.3 成果案例

1）苹果公司的Siri、亚马逊的Alexa和谷歌助手：口头提问
2）精确识别语音
3）物体识别
4）游戏
5）自动驾驶汽车的发展

1.4 特点

1）深度学习的一个外在特点是端到端的训练
2）从含参数统计模型转向完全无参数的模型
3）相对其它经典的机器学习方法而言，深度学习的不同在于：对非最优解的包容、对非凸非线性优化的使用。
4）开源了许多优秀的软件库、统计模型和预训练网络。

2.预备知识

2.1 环境配置

Anaconda/juphyter/pytorch/pycharm

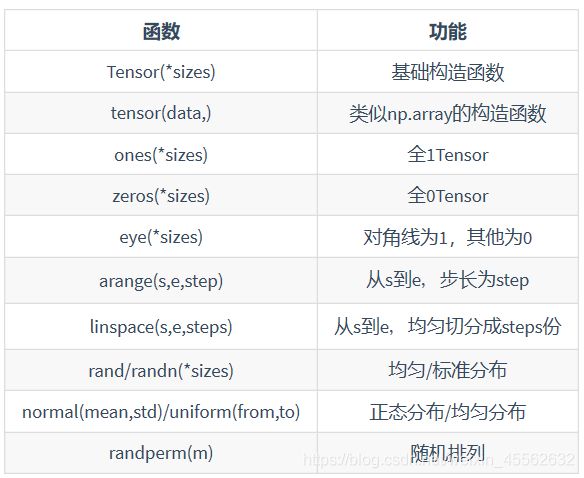
2.2 数据操作

1.创建tensor

2.操作
1）算术操作
在PyTorch中，同一种操作可能有很多种形式。
2）索引
索引出来的结果与原数据共享内存，也即修改一个，另一个会跟着修改。高级选择函数：

3）改变形状
用view()来改变Tensor的形状：
4）线性代数：

3.广播机制
当对两个形状不同的Tensor按元素运算时，可能会触发广播（broadcasting）机制：先适当复制元素使这两个Tensor形状相同后再按元素运算。
4.运算的内存开销
索引操作是不会开辟新内存的，而像y = x + y这样的运算是会新开内存的，然后将y指向新内存。
5.Tensor和NumPy相互转换
我们很容易用numpy()和from_numpy()将Tensor和NumPy中的数组相互转换。但是需要注意的一点是： 这两个函数所产生的的Tensor和NumPy中的数组共享相同的内存（所以他们之间的转换很快），改变其中一个时另一个也会改变！！！
6.Tensor on GPU
用方法to()可以将Tensor在CPU和GPU（需要硬件支持）之间相互移动。

2.3 自动求梯度

在深度学习中，我们经常需要对函数求梯度（gradient）。PyTorch提供的autograd包能够根据输入和前向传播过程自动构建计算图，并执行反向传播。
不允许张量对张量求导，只允许标量对张量求导，求导结果是和自变量同形的张量。

3.深度学习基础

3.1线性回归

线性回归输出是一个连续值，因此适用于回归问题。softmax回归则适用于分类问题。

线性回归和softmax回归都是单层神经网络。
1.线性回归的基本要素
1）模型定义

2）模型训练
训练数据、损失函数、优化算法
在机器学习里，将衡量误差的函数称为损失函数（loss function）。这里使用的平方误差函数也称为平方损失（square loss）。
解析解与数值解区别
小批量随机梯度下降（mini-batch
stochastic gradient descent）
3）模型预测
2.线性回归的表示方法
1）神经网络图

这里的输出层又叫全连接层（fully-connected layer）或稠密层（dense layer）。
2）矢量计算表达式
结果很明显，后者比前者更省时。因此，我们应该尽可能采用矢量计算，以提升计算效率。

3.2线性回归从零开始实现

仅使用Tensor和autograd模块就可以很容易地实现一个模型。
3.2.1 生成数据集
3.2.2 读取数据
3.2.3 初始化模型参数
我们将权重初始化成均值为0、标准差为0.01的正态随机数，偏差则初始化成0。
3.2.4 定义模型
3.2.5 定义损失函数
3.2.6 定义优化算法
3.2.7 训练模型

3.3线性回归的简洁实现

3.3.1 生成数据集
3.3.2 读取数据
3.3.3 定义模型
在上一节从零开始的实现中，我们需要定义模型参数，并使用它们一步步描述模型是怎样计算的。当模型结构变得更复杂时，这些步骤将变得更繁琐。其实，PyTorch提供了大量预定义的层，这使我们只需关注使用哪些层来构造模型。
3.3.4 初始化模型参数
3.3.5 定义损失函数
3.3.6 定义优化算法
3.3.7 训练模型
学习率lr、迭代周期个数num_epochs
torch.utils.data模块提供了有关数据处理的工具，torch.nn模块定义了大量神经网络的层，torch.nn.init模块定义了各种初始化方法，torch.optim模块提供了很多常用的优化算法。

3.4softmax回归

3.4.1 分类问题
3.4.2 softmax回归模型

因此softmax运算不改变预测类别输出。
3.4.3 单样本分类的矢量计算表达式

3.4.4 小批量样本分类的矢量计算表达式

3.4.5 交叉熵损失函数
交叉熵：

交叉熵损失函数：
3.4.6 模型预测及评价
准确率

3.5图像分类数据集（Fashion-MNIST）

相关有用的包：
1.torchvision.datasets: 一些加载数据的函数及常用的数据集接口；
2.torchvision.models: 包含常用的模型结构（含预训练模型），例如AlexNet、VGG、ResNet等；
3.torchvision.transforms: 常用的图片变换，例如裁剪、旋转等；
4.torchvision.utils: 其他的一些有用的方法。
3.5.1 获取数据集
3.5.2 读取小批量

3.6softmax回归的从零开始实现

3.6.1 获取和读取数据
3.6.2 初始化模型参数
3.6.3 实现softmax运算
3.6.4 定义模型
3.6.5 定义损失函数
3.6.6 计算分类准确率
3.6.7 训练模型
3.6.8 预测

3.7softmax回归的简洁实现

3.7.1 获取和读取数据
3.7.2 定义和初始化模型
3.7.3 softmax和交叉熵损失函数
3.7.4 定义优化算法
3.7.5 训练模型
1）PyTorch提供的函数往往具有更好的数值稳定性。
2）可以使用PyTorch更简洁地实现softmax回归。

3.8多层感知机

3.8.1 隐藏层

5个隐藏单元
隐藏层（hidden layer）
3.8.2 激活函数

即便再添加更多的隐藏层，以上设计依然只能与仅含输出层的单层神经网络等价。
全连接层只是对数据做仿射变换（affine transformation），而多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法是引入非线性变换，例如对隐藏变量使用按元素运算的非线性函数进行变换，然后再作为下一个全连接层的输入。
1.ReLU函数

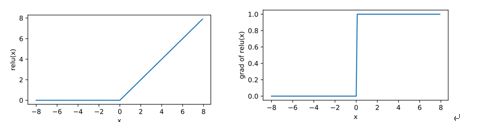
2. sigmoid函数

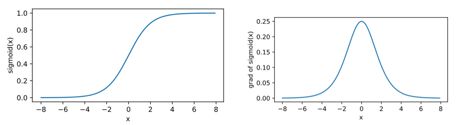
sigmoid函数可以将元素的值变换到0和1之间
3. tanh（双曲正切）函数

tanh（双曲正切）函数可以将元素的值变换到**-1和1**之间

虽然该函数的形状和sigmoid函数的形状很像，但tanh函数在坐标系的原点上对称。
3.8.3 多层感知机

3.9多层感知机从零开始实现

3.9.1 获取和读取数据
Fashion-MNIST数据集
3.9.2 定义模型参数
3.9.3 定义激活函数
3.9.4 定义模型
3.9.5 定义损失函数
3.9.6 训练模型
可以通过手动定义模型及其参数来实现简单的多层感知机。
当多层感知机的层数较多时，本节的实现方法会显得较烦琐，例如在定义模型参数的时候。

3.10多层感知机的简洁实现

3.10.1 定义模型
和softmax回归唯一的不同在于，我们多加了一个全连接层作为隐藏层。它的隐藏单元个数为256，并使用ReLU函数作为激活函数。
3.10.2 读取数据并训练模型

3.11 模型选择、欠拟合和过拟合

3.11.1 训练误差和泛化误差

区分训练误差（training
error）和泛化误差（generalization
error）。
前者指模型在训练数据集上表现出的误差，后者指模型在任意一个测试数据样本上表现出的误差的期望。
计算训练误差和泛化误差可以使用之前介绍过的损失函数，例如线性回归用到的平方损失函数和softmax回归用到的交叉熵损失函数。
3.11.2 模型选择
1.验证数据集（验证集）
2.K折交叉验证
3.11.3 欠拟合和过拟合
1.模型复杂度

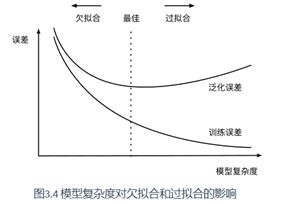
2.训练数据集的大小
3.11.4 多项式函数拟合实验
1）生成数据集
2）定义训练和测试模型
3）三阶多项式函数拟合（正常）
4）线性函数拟合（欠拟合）

5）训练样本不足（过拟合）

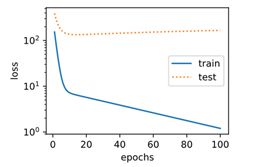
3.12 权重衰减

解决过拟合的方法——权重衰减
3.12.1 方法
L2​范数正则化又叫权重衰减

超参数λ>0。当权重参数均为0时，惩罚项最小。当λ较大时，惩罚项在损失函数中的比重较大，这通常会使学到的权重参数的元素较接近0。当λ设为0时，惩罚项完全不起作用。
3.12.2 高维线性回归实验
3.12.3 从零开始实现
1）初始化模型参数
2）定义L2范数惩罚项
3）定义训练和测试
4）观察过拟合
5）使用权重衰减
3.12.4 简洁实现
通过weight_decay参数来指定权重衰减超参数。默认下，PyTorch会对权重和偏差同时衰减。我们可以分别对权重和偏差构造优化器实例，从而只对权重衰减。

3.13 丢弃法

丢弃法（dropout） 来应对过拟合问题。本节中提到的丢弃法特指倒置丢弃法（inverted dropout）。
3.13.1 方法

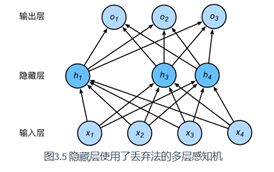
在测试模型时，我们为了拿到更加确定性的结果，一般不使用丢弃法。
3.13.2 从零开始实现
下面的dropout函数将以drop_prob的概率丢弃X中的元素。
1）定义模型参数
2）定义模型
3）训练和测试模型
3.13.3 简洁实现
小结：
我们可以通过使用丢弃法应对过拟合。
丢弃法只在训练模型时使用。

3.14 正向传播、反向传播和计算图

3.14.1 正向传播
3.14.2 正向传播的计算图

3.14.3 反向传播
链式法则
3.14.4 训练深度学习模型
在模型参数初始化完成后，我们交替地进行正向传播和反向传播，并根据反向传播计算的梯度迭代模型参数。既然我们在反向传播中使用了正向传播中计算得到的中间变量来避免重复计算，那么这个复用也导致正向传播结束后不能立即释放中间变量内存。
这些中间变量的个数大体上与网络层数线性相关，每个变量的大小跟批量大小和输入个数也是线性相关的。
小结：
正向传播沿着从输入层到输出层的顺序，依次计算并存储神经网络的中间变量。
反向传播沿着从输出层到输入层的顺序，依次计算并存储神经网络中间变量和参数的梯度。
在训练深度学习模型时，正向传播和反向传播相互依赖。

3.15 数值稳定性和模型初始化

3.15.1 衰减和爆炸
举个例子，假设输入和所有层的权重参数都是标量，如权重参数为0.2和5，多层感知机的第30层输出为输入X分别与0.230（衰减）和530≈9×1020（爆炸）的乘积。类似地，当层数较多时，梯度的计算也更容易出现衰减或爆炸。
3.15.2 随机初始化模型参数
1）PyTorch的默认随机初始化
2）Xavier随机初始化
假设某全连接层的输入个数为a，输出个数为b，Xavier随机初始化将使该层中权重参数的每个元素都随机采样于均匀分布：

3.16 实战Kaggle比赛：房价预测

3.16.1 Kaggle比赛
3.16.2 获取和读取数据集
3.16.3 预处理数据
连续数值的特征做标准化（standardization）
3.16.4 训练模型
使用一个基本的线性回归模型和平方损失函数来训练模型。
3.16.5 K折交叉验证
调参
3.16.6 模型选择
3.16.7 预测并在Kaggle提交结果