时间序列分析笔记——VAR

利用 MTS 包的 VAR() 函数估计 VAR(1) 模型：

library(MTS)

Z <- coredata(as.xts(ts.gdp3r))
m1.gdp3r <- VAR(Z, 1)

估计 VAR(2) 模型：

m2.gdp3r <- VAR(Z, 2)

VAR(1) 的 AIC 为 −3.46 ， VAR(2) 的 AIC 为 −3.50, VAR(2) 占优。

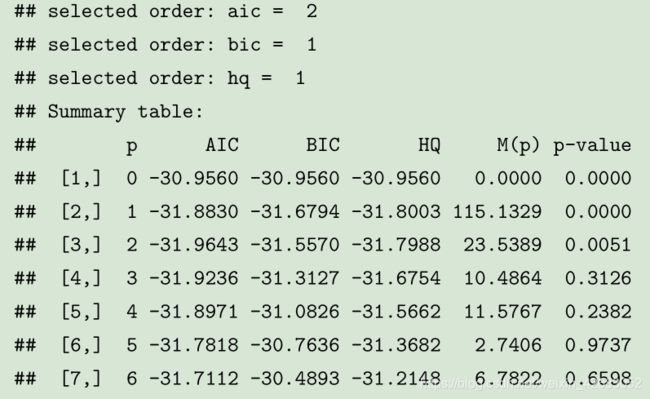
利用 MTS 包的 VARorder 函数可以计算 VAR 定阶的 M(i) 统计量检验和各种信息准则：

m3.gdp3r <- VARorder(Z/100)

从 AIC 比较来看，应该取 p = 2 。从检验来看，从 i = 3 阶开始 Φ i 就不显著了，但 Φ 1 和 Φ 2 显著，所以应该取 p = 2 阶。

模型检验

可以计算模型残差，对残差进行多元白噪声检验（多元混成检验）。残差的多元混成检验因为使用了估计的参数，所以统计量的自由度会减少 k 2 p ，这是系数矩阵 Φ j , j = 1,2,...,p 中的参数个数。如果系数矩阵中某些参数固定为 0 ，应按无约束的参数个数计算要扣除的自由度。在 MTS 包的 mq() 函数中用 adj= 指定需要减少的自由度。 

VAR(2) 模型的残差的多元混成检验程序如下：

resi <- m2.gdp3r$residuals
mq(resi, adj=3^2 * 2)

检验结果只有在滞后 4 显著，基本可以认为模型是充分的。
对残差还可以进行异方差等检验。

模型简化

当 VAR 中分量个数 k 较大时，模型有许多参数，系数矩阵中参数个数为 k 2 p 个。如果没有先验知识要求参数非零，可以将不显著的参数约束为零再估计。
模型简化没有公认的最优做法。一种办法是计算参数估计值与标准误差的比值，称为 t 比值，将 t 比值绝对值小于 1.645( 相当于 0.10 检验水平 ) 或者小于 1.96 （相当于 0.05 检验水平）的系数设置为零。 MTS 包的VARchi() 函数输入多元时间序列和 VAR 的阶，以及thres=1.645 或 thres=1.96 这样的 t 比值界限，返回可设置为零的个数，以及这些参数同时等于零的零假设的卡方检验结果。

VARchi(Z, 2, thres=1.645)

VARchi(Z, 2, thres=1.96)

结果表明在 0.10 水平下，逐个检验有 8 个参数不显著，如果检验这 8 个参数同时等于零的零假设， p 值为0.056 ，可以同时设这 8 个参数等于 0 。如果在 0.05 水平下逐个检验有 10 个参数不显著，但是其同时等于零的检验的 p 值为 0.0005 ，所以不能同时将 10 个参数删去。 

MTS 包的 refVAR() 输入一个无约束的 VAR 模型的结果，以及 thres=1.96 这样的 t 比值界限，生成设置部分系数为零的约束估计结果。可以通过 AIC 比较完全模型和约束模型。如：

mods1.gdp3r <- VAR(Z, 2)

mods2.gdp3r <- refVAR(mods1.gdp3r, thres=1.96)

无约束的 VAR(2) 的 AIC 值为 −3.50 ，约束 10 个参数为零的 VAR(2) 的 AIC 值为 −3.53 ，所以约束模型较优。

对这个简化的模型的检验，可以提取残差后用 MTS::mq() 函数检验，这时自由度缩减个数由原来的 3 2 ×2 =18 个，减少到 9 个，因为模型中约束了 9 个参数等于零。 MTS 包还提供了一个 MTSdiag() 函数，输入模型结果和 adj= 自由度缩减个数，作残差的 CCM 估计表、图和残差的多元混成检验：

MTSdiag(mods2.gdp3r, adj=9)

从残差的 CCM 和多元混成检验结果来看，约束的模型是充分的。

残差的相关阵计算程序：
cor(mods2.gdp3r$residuals)

格兰杰因果性检验

如果模型可以简化为某些代表格兰杰因果性的系数等于零，则可以据此进行格兰杰因果性的检验。在二元的VAR(1) 模型中，如果约束 ϕ 12 (1) = 0 后的模型与无约束模型没有显著差异，则 r 2t 不是 r 1t 的格兰杰原因。 p 阶和 k 元的情形类似。
为了比较无约束与约束的模型，使用对数似然比检验，得到的统计量在约束参数等于零的零假设下渐近服从卡方分布。
MTS 包中 GrangerTest() 函数执行格兰杰因果性检验，默认第一个分量为单向的格兰杰原因，可以用locInput= 序号指定哪一个或者哪几个分量作为原因。

GrangerTest(Z, p=2, locInput=3)

结果 p 值小于 0.05 ，说明英国和加拿大也是美国的格兰杰原因。

GrangerTest(Z, p=2, locInput=2)

结果表明美国和英国是加拿大的格兰杰原因。

GrangerTest(Z, p=2, locInput=1)

综合以上三个结果，在 0.05 水平下英国是美国和加拿大的格兰杰原因，加拿大和美国不是英国的格兰杰原因，可以认为英国是美国和加拿大单向的格兰杰原因。结果中给出了约束系数等于零的模型估计结果。

VAR 的预测

第一个预测对应 2011 年第三季度，最后一个预测对应 2013 年第二季度。

VARpred(m2.gdp3r, 8)

colMeans(Z)#多步预测会趋近到序列均值，计算序列均值

apply(Z, 2, sd)#计算序列的样本标准差

VAR 的脉冲响应函数

VARirf(mods2.gdp3r$Phi, mods2.gdp3r$Sig, orth=FALSE)

VARirf(mods2.gdp3r$Phi, mods2.gdp3r$Sig, orth=TRUE)#这三个分量的新息的即期相关不大，所以正交化的脉冲响应与原始的表现相近。