Android -- Magical ProgressBar 2.0

前不久写了一个六边形的进度条，个人感觉仍旧有很多美中不足（好吧，这里把“美中”去掉 - -）的地方，比如说像之前一位同事提到的View绘制边界其实线条有一半是无法显示的。所以在这此的代码中将这个问题考虑了进去，而且UI设计师认为平角六边形的效果有些粗糙，这里改成了圆角。还有就是先前的版本代码上过于冗余，这里也尽我所能的简化了下代码。这里说下思路，具体的实现细节可以在文章的结尾处下载源码。
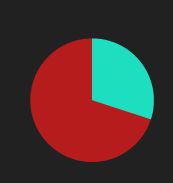
先简单的看一下效果图：

效果图

实现步骤

首先，我们在最底层放上一个扇形的进度条
（github下载地址：https://github.com/timqi/SectorProgressView）。

Android -- Magical ProgressBar 2.0_第2张图片

步骤1

2.将一张圆角六边形的图片覆盖在上面

Android -- Magical ProgressBar 2.0_第3张图片

步骤2

3.在盖上一张这样的图片把多余的部分遮住。

Android -- Magical ProgressBar 2.0_第4张图片

步骤三3

就像这样

Android -- Magical ProgressBar 2.0_第5张图片

成果

怎么样？是不是感觉so easy..... : )
.
.
.
.
.
.
.
.
呵呵。。。。。。怎么可能 - - 。
.
.
.
.
.
.
.
好吧，我承认，其实我一开始就想用这个方法蒙混过关的，毕竟，我比较懒。（UI那边看过也说这个可以通过，怎么说这个方案如果没有他切片我也无法实行- -）。但是在我给ios端开发的同事确认方案的时候，一切都变了- -，只听他淡淡的飘出了一个字，鄙视中带着蔑视，蔑视中带着无视。。。。。。：好丑，你这进度条下来是歪的啊? 然后他默默的在网上找了个开源的解决了这个歪的问题。- -

Android -- Magical ProgressBar 2.0_第6张图片

就像这样

（丑就算了，他竟然还加了一个修饰词），不过不是他的提醒，我也不会想到把这个进度条认认真真的重头写一遍。

好了，废话到这里 (毕竟在描述一个故事的时候总要交代下故事背景)，接下来进入正题。

公共API

 /**
  * 设置进度
  *
  * @param progress 当前进度
  */
 public void setProgress(float progress) 
 
 /**
   * 设置进度条的宽度
   *
   * @param width 进度条的宽度 dp值
  */
  public void setProgressWith(float width) 

/**
  * 设置中央背景的颜色
  *
  * @param color 中央背景颜色
  */
 public void setCenterColor(int color) 

 /**
  * 设置已完成进度条的颜色
  *
  * @param color 已完成的进度条颜色
 */

 public void setFinishedColor(int color)

 /**
  * 设置未完成进度条的颜色
  *
  * @param color 未完成的进度条的颜色
  */
 public void setUnfinishedColor(int color)

没兴趣的朋友下面的内容都可以省略并直接翻到文末，点击相应链接下载控件即可。

点的计算

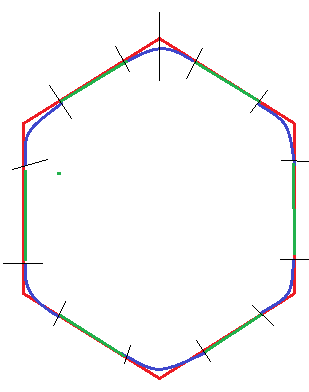
首先，我们先考虑绘制未完成的进度条，和中间的背景图案。这里我们可以明确的看出，轨迹是由六条60°的圆弧和六条线段组成。所在在绘制之前，我们需要确定圆角的六个圆弧所在的圆的位置，也就是RecfF中的（left，top，right，bottom）的参数（此处具体参照自定义View中是如何绘制圆弧的，google or baidu），即每个圆所在外切矩形的左上角坐标和右下角的坐标。和每段圆弧连接的线段的两个端点的的坐标。也就是总共24个点的坐标。由于边界显示只会显示一半线宽的问题，这里我们在边界处计算坐标的时候还要考虑到线粗的问题，顶部和左边分别考虑到纵坐标和横坐标加上一半线宽，底部和右边则考虑在纵坐标和横坐标上减去一半的线宽。
关于24个点的坐标的计算具体代码如下，此处 l 表示此圆角六边形所在的外切平角正六边形的长度，r 则表示圆弧所在圆的半径。mProgressWidth表示进度条宽度的一半。

具体怎么计算的这里参考下图and代码。

具体计算流程.png

/**
 * 初始化各个点
 */
 private void initPoints() {
       //六条线段的十二个端点，从进度开始位置的第一条线段开始顺时针计算
       linePoints = new PointView[12];
       linePoints[0] = new PointView((float) (l * cos30 - r * tan30 * cos30 + r),
             (float) (r * tan30 * sin30 + mProgressWidth));
       linePoints[1] = new PointView((float) (l * cos30 * 2 - r * tan30 * cos30 - 
              mProgressWidth),  (float) (l * sin30 - r * tan30 * sin30));
       linePoints[2] = new PointView((float) (l * cos30 * 2 - mProgressWidth),
             (float) (l * sin30 + r * tan30));
       linePoints[3] = new PointView((float) (l * cos30 * 2 - mProgressWidth),
             (float) (l * sin30 + l - r * tan30));
       linePoints[4] = new PointView((float) (l * cos30 * 2 - r * tan30 * cos30 - 
              mProgressWidth), (float) (l * sin30 + l + r * tan30 * sin30));
       linePoints[5] = new PointView((float) (l * cos30 + r * tan30 * cos30),
             (float) (l * sin30 * 2 + l - r * tan30 * sin30 - mProgressWidth));
         linePoints[6] = new PointView((float) (l * cos30 - r * tan30 * cos30),
            (float) (l * sin30 * 2 + l - r * tan30 * sin30 - mProgressWidth));
       linePoints[7] = new PointView((float) (r * sin30 + mProgressWidth),
             (float) (l * sin30 + l + r * tan30 * sin30));
       linePoints[8] = new PointView(0 + mProgressWidth,
             (float) (l * sin30 + l - r * tan30));
       linePoints[9] = new PointView(0 + mProgressWidth,
             (float) (l * sin30 + r * tan30));
       linePoints[10] = new PointView((float) (r * sin30 + mProgressWidth),
             (float) (l * sin30 - r * tan30 * sin30));
       linePoints[11] = new PointView((float) (l * cos30 - r * tan30 * cos30),
             (float) (r * tan30 * sin30 + mProgressWidth));

 
       //六条圆弧的所在的圆的外接矩形的左上角坐标和右下角坐标（用于确定远的位置），
       //从进度开始位置的第一条圆弧开始顺时针计算
      arcPoints = new PointView[12];
      arcPoints[0] = new PointView((float) (l * cos30 - r),
           (float) (r / cos30 - r + mProgressWidth));
      arcPoints[1] = new PointView((float) (l * cos30 + r),
           (float) (r / cos30 - r + 2 * r + mProgressWidth));
      arcPoints[2] = new PointView((float) (l * cos30 * 2 - r * 2 - mProgressWidth),
           (float) (l * sin30 + r * tan30 - r));
       arcPoints[3] = new PointView((float) (l * cos30 * 2 - mProgressWidth),
         (float) (l * sin30 + r * tan30 + r));
       arcPoints[4] = new PointView((float) (l * cos30 * 2 - r * 2 - mProgressWidth),
           (float) (l * sin30 + l - r * tan30 - r));
       arcPoints[5] = new PointView((float) (l * cos30 * 2 - mProgressWidth),
           (float) (l * sin30 + l - r * tan30 + r));
      arcPoints[6] = new PointView((float) (l * cos30 - r),
            (float) (l * sin30 * 2 + l - r / cos30 - r - mProgressWidth));
      arcPoints[7] = new PointView((float) (l * cos30 + r),
            (float) (l * sin30 * 2 + l - r / cos30 + r - mProgressWidth));
      arcPoints[8] = new PointView(0 + mProgressWidth,
           (float) (l * sin30 + l - r * tan30 - r));
      arcPoints[9] = new PointView(r * 2 + mProgressWidth,
           (float) (l * sin30 + l - r * tan30 + r));
      arcPoints[10] = new PointView(0 + mProgressWidth,
           (float) (l * sin30 + r * tan30 - r));
      arcPoints[11] = new PointView(r * 2 + mProgressWidth,
           (float) (l * sin30 + r * tan30 + r));

 }

绘制背景和未完成的进度条轨迹

计算出这些点的坐标后我们就可以调用canvas中的drawArc()和drawLine()方法来绘制圆弧和线段了，为了使代码看上去更简洁，我们这里可以通过循环来做。将这写坐标放到数组中也是为了方便循环。

 /**
   * 画未完成的进度条
   */
 private void drawUnfinishedProgress(Canvas canvas) {
       for (int i = 0; i < 6; i++) {
             RectF rectF = new RectF(arcPoints[i * 2].x, arcPoints[i * 2].y,
                    arcPoints[i * 2 + 1].x, arcPoints[i * 2 + 1].y);
             canvas.drawArc(rectF, -120 + i * 60, 60, false, mUnfinishedPaint);
             canvas.drawLine(linePoints[i * 2].x, linePoints[i * 2].y,
             linePoints[i * 2 + 1].x, linePoints[i * 2 + 1].y, mUnfinishedPaint);
        }
 }

   /**
    * 画背景
    */
 private void drawBg(Canvas canvas) {
        //线段部分
       Path path = new Path();
       path.moveTo(linePoints[0].x, linePoints[0].y);
       for (int i = 1; i < 12; i++) {
             path.lineTo(linePoints[i].x, linePoints[i].y);
        }
       path.close();
       canvas.drawPath(path, mBgPaint);
      
        //圆弧部分
       for (int i = 0; i < 6; i++) {
              RectF rectF = new RectF(arcPoints[i * 2].x, arcPoints[i * 2].y,
               arcPoints[i * 2 + 1].x, arcPoints[i * 2 + 1].y);
               canvas.drawArc(rectF, -120 + i * 60, 60, true, mBgPaint);
         }
 }

进度条的绘制

1.进度区间的划分

接下来就是一个最复杂的部分，也就是具体进度的绘制。首先这里的第一段圆弧是特殊的，因为进度条开始是以第一段圆弧的中点作为起点，顺时针走，直到回到第一段圆弧的中点。这里我将进度条分成了十三个区间，起点到每一个区间右边界轨迹的长度与整个图形的周长比作为具体进度区间的范围。如下图所示。

Android -- Magical ProgressBar 2.0_第7张图片

进度条的划分.png

具体代码如下：mc代表的是每段弧的长度，ml则代表每条线段的长度（这里再次说明之前的l 表示是圆角六边形所对应的外接平角六边形的边长）。

 /**
  * 进度节点的计算
 */
 private void calculateProgress() {
      mc = (float) (PI * r * 2 / 6);
      ml = (float) (l - (r * tan30 * 2));
      c = (float) (PI * r * 2 + 6 * ml);
      progressParts[0] = ((mc / 2) / c) * 100;
      for (int i = 1; i < 12; i++) {
           if (i % 2 == 1) {
                 progressParts[i] = progressParts[i - 1] + ml / c * 100;
           } else if (i % 2 == 0) {
                 progressParts[i] = progressParts[i - 1] + mc / c * 100;
           }
      }
      progressParts[12] = 100;
 }

这里我们将所有的区间打印出来看一下结果。

D/MagicalProgress: 区间范围：(0 ,1.7836796]
D/MagicalProgress: 区间范围：(1.7836796 ,14.882988]
D/MagicalProgress: 区间范围：(14.882988 ,18.450348]
D/MagicalProgress: 区间范围：(18.450348 ,31.549656]
D/MagicalProgress: 区间范围：(31.549656 ,35.117016]
D/MagicalProgress: 区间范围：(35.117016 ,48.216324]
D/MagicalProgress: 区间范围：(48.216324 ,51.783684]
D/MagicalProgress: 区间范围：(51.783684 ,64.882996]
D/MagicalProgress: 区间范围：(64.882996 ,68.450356]
D/MagicalProgress: 区间范围：(68.450356 ,81.54967]
D/MagicalProgress: 区间范围：(81.54967 ,85.11703]
D/MagicalProgress: 区间范围：(85.11703 ,98.21634]
D/MagicalProgress: 区间范围：(98.21634 ,100.0]

2.绘制已完成的轨迹

每次当我们的进度条走到一个新的区间的时候，我们要将之前走过的区间填充完整，举个栗子，当我们的进度走到34%的时候，我们处在第四个区间，这里我们还要将前三个区间的轨迹也绘制好。具体代码如下。

 /**
   * 绘制已完成的轨迹
   *
   * @param index 所处区间的上一个区间的索引
   */
 private void drawTrail(Canvas canvas, int index) {
     if (index < 0 || index > 13) {
           throw new IllegalArgumentException("the index must 
                        less than 14 and more than 0");
     }
     for (int i = 0; i < index; i++) {
            //头部
           if (i == 0) {
               RectF rectF = new RectF(arcPoints[0].x, arcPoints[0].y,
                           arcPoints[1].x, arcPoints[1].y);
               canvas.drawArc(rectF, -90, 30, false, mFinishedPaint);
            //线段部分
           } else if (i % 2 == 1) 
                canvas.drawLine(linePoints[i - 1].x, linePoints[i - 1].y,
                linePoints[i].x, linePoints[i].y, mFinishedPaint);
            //圆弧部分
           } else if (i != 0 && i != 12 && i % 2 == 0) {
                   RectF rectF = new RectF(arcPoints[i].x, arcPoints[i].y,
                   arcPoints[i + 1].x, arcPoints[i + 1].y);
                   canvas.drawArc(rectF, -120 + i * 30, 60, false, mFinishedPaint);
            //尾部
           } else if (i == 12) {
                 RectF rectF = new RectF(arcPoints[0].x, arcPoints[0].y,
                 arcPoints[1].x, arcPoints[1].y);
                 canvas.drawArc(rectF, -120, 30, false, mFinishedPaint);
            }
       }
 }

3.进度条的绘制

接下来我们就可以进行进度条的绘制了，进度条区间如果处在圆弧内，我们只要算出现在进度占所在区间的比例（参照公式p的计算方法）再乘以60度，让他绘制对应角度的圆弧即可。至于线段可能会超微复杂一点。可以参照下图，p为当前进度占所在区间的百分比，(x, y)指当前进度所在的坐标。

p 的计算公式：

float percent = (mProgress - progressParts[i]) /
                     (progressParts[i + 1] - progressParts[i]);

Android -- Magical ProgressBar 2.0_第8张图片

线段区间进度条计算过程

之后得出了如下的通项公式：
**x = x(i) + [x(i+1) - x(i)] * p **
**y = y(i) + [y(i+1) - y(i)] * p **
有了通项之后我们明显这里采用循环的方法来简洁代码（好吧- -，我承认，之前那个确实就是坨shit），由于首尾比较特殊，特别我们这里头部和尾部单独拎出来做：

 /**
 * 画进度条
 */
 private void drawProgress(Canvas canvas) {
    //头部的绘制
     if (mProgress > 0 && mProgress <= progressParts[0]) {    
         RectF rectFOne = new RectF(arcPoints[0].x, arcPoints[0].y,
         arcPoints[1].x, arcPoints[1].y);
         float oval = mProgress / progressParts[0] * 30;
         canvas.drawArc(rectFOne, -90, oval, false, mFinishedPaint);
     }
     for (int i = 0; i < 11; i++) {
         if (mProgress > progressParts[i] && mProgress <= progressParts[i + 1]) {
               drawTrail(canvas, i + 1);
               float percent = (mProgress - progressParts[i]) /
                                  (progressParts[i + 1] - progressParts[i]);
                //线段部分的绘制
               if (i % 2 == 0) {
                    canvas.drawLine(linePoints[i].x, linePoints[i].y,
                    linePoints[i].x + ((linePoints[i + 1].x - linePoints[i].x) * percent),
                    linePoints[i].y + ((linePoints[i + 1].y - linePoints[i].y) * percent), 
                    mFinishedPaint);
                //圆弧部分的绘制
               } else if (i % 2 == 1) {
                      RectF rectF = new RectF(arcPoints[i + 1].x, arcPoints[i + 1].y,
                      arcPoints[i + 2].x, arcPoints[i + 2].y);
                      float oval = percent * 60;
                 canvas.drawArc(rectF, -120 + (i + 1) * 30, oval, false, mFinishedPaint)
               }
          }
     }

      //尾部的绘制
     if (mProgress > progressParts[11] && mProgress <= 100) {
         drawTrail(canvas, 12);
         float percent = (mProgress - progressParts[11]) / (100 - progressParts[11]);
         RectF rectFOne = new RectF(arcPoints[0].x, arcPoints[0].y,
         arcPoints[1].x, arcPoints[1].y);
         float oval = percent * 30;
         canvas.drawArc(rectFOne, -120, oval, false, mFinishedPaint);
     }
 }

一脸懵逼和懒得看朋友（老实讲，要不是我自己写的，我肯定会是一脸懵逼和懒得看的里面的一种 - -）可以直接通过下方链接下载控件，并在需要的时候应用到项目里。

https://github.com/HandGrab/MagicalProgress