基于区间算法的像素函数绘图方法（附matlab代码）（仿GrafEq）

惯例声明：本人没有相关的工程应用经验，只是纯粹对相关算法感兴趣才写此博客。所以如果有错误，欢迎在评论区指正，不胜感激。本文主要关注于算法的实现，对于实际应用等问题本人没有任何经验，所以也不再涉及。

0 前言

这个文章写作目的是很久之前看到了Matrix67的一篇博客，介绍一款软件叫GrafEq。
http://www.matrix67.com/blog/archives/4447#more-4447
和常规的数学软件不同，它不是给出一些离散点，然后进行连线。它是基于像素级别的绘制定义域内的图像。因此，它可以做到只要能写出函数表达式，就一定能绘制出图像，无论是隐函数还是什么其它复杂函数。

现在它的官网依然存在，可以体验一下。
http://www.peda.com/grafeq/
下面是官网中一个示例函数，还有很多神奇的图像也是根据函数绘制的，这里就不再介绍了。

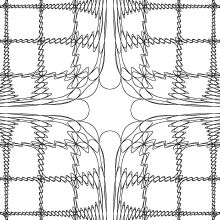
当然，最近突然想起这个茬了，就大概看了看基本原理，自己仿照着算法做了一款基于matlab的图像绘制程序。

参考文献：
Reliable Two-Dimensional Graphing Methods for Mathematical Formulae with Two Free Variables (作者：Jeff Tupper)

1 算法原理

1.1 判断该像素是否是解

首先把每一个像素都考虑其长和宽，以一个区间的形式来描述。
这种算法是基于区间分析，当区间内存在解的时候，或者不确定区间内是否存在解的时候，将像素所代表的区间标为解。当区间内不存在解的时候，将像素所代表的区间标为背景。

其中像素所代表的区间，可以举例说明：
比如像素在x轴上的坐标为0,1,2,3,4…
则每一个像素对应的区间为[-0.5,0.5]，[0.5,1.5]，[1.5,2.5]…

对于输入的函数，我们最终可以把函数表示为下面的形式：
f(x,y)>g(x,y)或f(x,y) 比如y=x^ 2-1，其中f(x,y)=y，g(x,y)=x^2-1

根据区间算法，可以得出2个逻辑值T和F。
以小于<为例，[a,b]<[A,B]（这里默认a 如果b 如果B 如果两个区间存在交集，则返回[T,F]。

之后，所有返回[F,F]的标记为确定区间不存在解。所有返回[T,T]的标记为确定区间存在解。所有返回[T,F]的标记为不确定是否存在解。

1.2 算法示例

以y

如果像素是1×1像素，则这个像素点x区间为[-4,4]，y区间为[-4,4]
计算式左侧为[-4,4]，计算式右侧为[-6,2]
进行判断[-4,4]<[-6,2]，区间存在交集，返回[T,F]。
说明有可能存在解。

如果像素是2×2像素，则遍历循环。
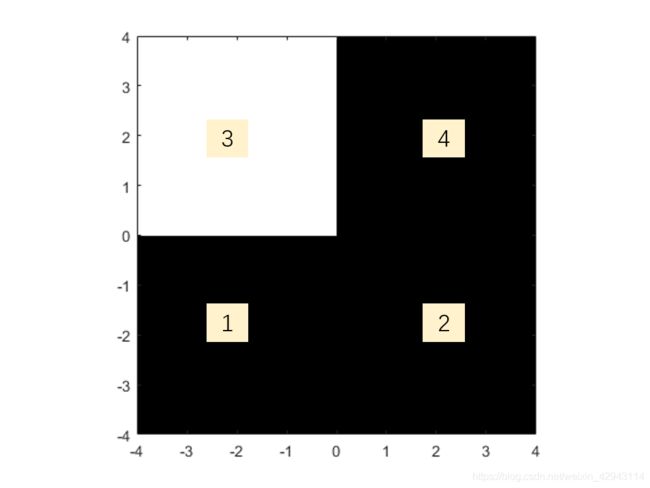
1号像素x区间为[-4,0]，y区间为[-4,0]
进行判断[-4,0]<[-6,-2]，区间存在交集，返回[T,F]。
2号像素x区间[0,4]，y区间为[-4,0]
进行判断[-4,0]<[-2,2]，区间存在交集，返回[T,F]。
3号像素x区间[-4,0]，y区间为[0,4]
进行判断[0,4]<[-6,-2]，区间完全大于另一个区间，返回[F,F]。
4号像素x区间[0,4]，y区间为[0,4]
进行判断[0,4]<[-2,2]，区间存在交集，返回[T,F]。

因此，我们可以绘制出2*2像素的图像：

同理，如果取更多的像素，则可以看到更精细的图像：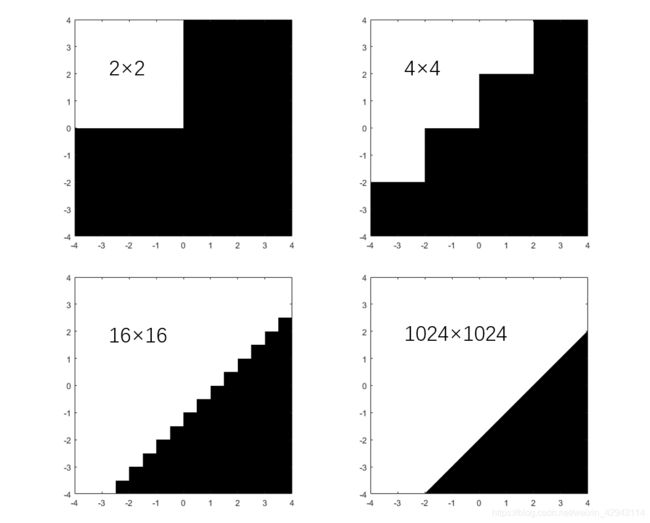

可以看到，当把像素取到1024×1024时，则看不到明显的像素值了。

1.3 区间算法

前面的是以yx，xy=x+sin(x)之类的。

比如f=x*y，对于区间运算，就是找到f可能的所有可能范围，以x[-1,2]，y[1,3]为例。x*y所能取到的最小值为-1*3=-3，x*y所能取到的最大值为2*3=6，因此[-1,2] *[1,3]=[-3,6]。

比如f=sin(x)，对于区间运算，同样是找到f可能的所有可能范围。以x[0,2]为例，最小值是0，最大值为1。因此，sin([0,2])=[0,1]。

其它区间算法就不再一一列举了。好像matlab内没有相关的计算，所以需要自己进行编程计算。

2 计算示例

以下面的函数
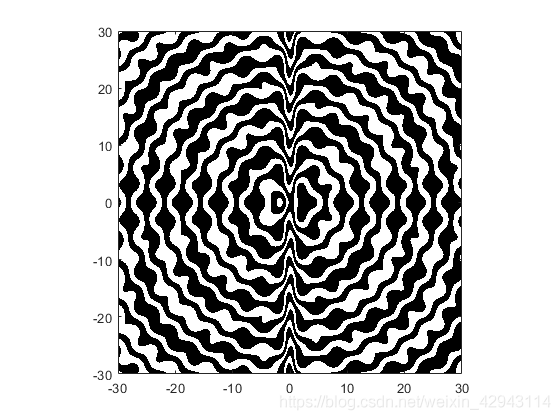
f(x,y) =cos(cos(min(sinx+y,x+siny))) − cos(sin(max(siny+x,y+sinx))) > 0
为例：

绘图区间x为[-10,10]，y为[-10,10]，总共划分为1024份。

绘图matlab代码如下：

clear
clc
close all
%定义求解区间
X=[-10,10];
Y=[-10,10];


%求解域的长与宽
W=X(2)-X(1);
H=Y(2)-Y(1);


N_Split=10;%分割10次，采用2分法
D_Split=2;%采用2分法

dX=W/D_Split^N_Split;
dY=H/D_Split^N_Split;
x=X(1):dX:X(2);
y=Y(1):dY:Y(2);
%定义本次切割的所有网格格点
Interval_k_Ind=Mesh2IntervalInd(x,y);
%0是未定义，1是确定存在解，2是确定不存在解
Solve=zeros(length(y)-1,length(x)-1);
%遍历循环
for m=1:size(Interval_k_Ind,1)
    x_I_New=Interval_k_Ind(m,1);
    y_I_New=Interval_k_Ind(m,2);
    X_I_k=x(x_I_New:x_I_New+1);
    Y_I_k=y(y_I_New:y_I_New+1);
    I_TF=I_Formula(X_I_k,Y_I_k);
    %然后是对结果的判断
    if xor(I_TF(1),I_TF(2))
        Solve(y_I_New,x_I_New)=0;
    elseif I_TF(1)==true && I_TF(2)==true
        Solve(y_I_New,x_I_New)=1;
    elseif I_TF(1)==false && I_TF(2)==false
        Solve(y_I_New,x_I_New)=2;
    end
    
end
Solve_Old=Solve;

    
%将所有等于0的替换为1
Solve(Solve==0)=1;
Solve=2-Solve;
%绘图
[X_Draw,Y_Draw]=meshgrid(0.5*(x(1:end-1)+x(2:end)),0.5*(y(1:end-1)+y(2:end)));
figure()
imagesc(0.5*(x(1:end-1)+x(2:end)),0.5*(y(1:end-1)+y(2:end)),Solve)
set(gca,'YDir','normal')
colormap([[1,1,1];[0,0,0]])%白色的是背景，解为黑色
shading flat
axis equal
xlim(X);ylim(Y);




function I_TF=I_Formula(I_x,I_y)
% %示例等式1：y < x-2
% I_TF=Less(I_y,I_x-2);

% %示例等式2：y > x*x-1
% I_TF=Greater(I_y,I_Multi(I_x,I_x)-1);

%示例等式3：f(x,y) =cos(cos(min(sinx+y,x+siny))) − cos(sin(max(siny+x,y+sinx))) > 0
F1=I_Cos(I_Cos(I_Min( I_PLUS(I_Sin(I_x),I_y) , I_PLUS(I_Sin(I_y),I_x))));
F2=I_Cos(I_Sin(I_Max( I_PLUS(I_Sin(I_y),I_x) , I_PLUS(I_Sin(I_x),I_y))));
I_TF=Greater(F1,F2);

end

function I_Save=Mesh2Interval(x,y)
[x2,y2]=meshgrid(x,y);
I_Save=zeros((length(x)-1)*(length(y)-1),4);
k=1;
for kx=1:length(x)-1
    for ky=1:length(y)-1
        %储存为x1,x2,y1,y2的形式
        I_Save(k,:)=[x2(ky,kx),x2(ky,kx+1),y2(ky,kx),y2(ky+1,kx)];
        k=k+1;
    end
end
end

function Indxy=Mesh2IntervalInd(x,y)
Nx=length(x);
Ny=length(y);
Indxy=zeros((Nx-1)*(Ny-1),2);
k=1;
for kx=1:Nx-1
    for ky=1:Ny-1
        %储存为x1,x2,y1,y2的形式
        Indxy(k,:)=[kx,ky];
        k=k+1;
    end
end
end


function I_TF=Greater(I_A,I_B)
%区间算法，A>B
if I_A(1)>I_B(2)
    I_TF=[true,true];
elseif I_A(2)I_B(2)
    I_TF=[false,false];
elseif I_A(2)I_B(2)
    I_TF=[false,false];
else 
    %两者存在交集
    I_TF=[false,true];
end
end


function I_C=I_PLUS(I_A,I_B)
%区间算法，A+B
I_C=[I_A(1)+I_B(1),I_A(2)+I_B(2)];
end

function I_C=I_MINUS(I_A,I_B)
%区间算法，A-B
I_B2=[-I_B(2),-I_B(1)];
I_C=I_PLUS(I_A,I_B2);
end

function I_C=I_Multi(I_A,I_B)
%区间算法，A*B
Multi_All=I_A'*I_B;
I_C=[min(min(Multi_All)),max(max(Multi_All))];
end

function I_C=I_Sin(I_A)
%区间算法，sin(x)
MinMax=[0,0];I_C=[0,0];
a=I_A(1);b=I_A(2);
%判断是否存在极大值
if floor((a/pi-0.5)/2)

3 计算示例2

对于某些计算结果，当确定区间内不存在解之后，可以直接跳过求解步骤，进而减少绘图时间。

因此可以进行循环，逐次加密进行求解。

matlab代码如下：

clear
clc
close all
%定义求解区间
X=[-10,10];
Y=[-10,10];


%求解域的长与宽
W=X(2)-X(1);
H=Y(2)-Y(1);


N_Split=10;%分割3次，采用2分法
D_Split=2;%采用2分法
for k=0:N_Split
    dX=W/D_Split^k;
    dY=H/D_Split^k;
    x=X(1):dX:X(2);
    y=Y(1):dY:Y(2);
    %定义本次切割的所有网格格点
    Interval_k_Ind=Mesh2IntervalInd(x,y);
    %Interval_k=Mesh2Interval(x,y);
    %0是未定义，1是确定存在解，2是确定不存在解
    Solve=zeros(length(y)-1,length(x)-1);
    %遍历循环
    if k==0
        %如果是第一次判断，直接求解
        I_TF=I_Formula(X,Y);
        if xor(I_TF(1),I_TF(2))
            Solve=0;
        elseif I_TF(1)==true && I_TF(2)==true
            Solve=1;
        elseif I_TF(1)==false && I_TF(2)==false
            Solve=2;
        end
    else
        for m=1:size(Interval_k_Ind,1)
            x_I_New=Interval_k_Ind(m,1);
            y_I_New=Interval_k_Ind(m,2);
            %判断在上一个区间内是否为0或者1
            x_I_Old=ceil(x_I_New/D_Split);
            y_I_Old=ceil(y_I_New/D_Split);
            if Solve_Old(y_I_Old,x_I_Old)==0 || Solve_Old(y_I_Old,x_I_Old)==1
                X_I_k=x(x_I_New:x_I_New+1);
                Y_I_k=y(y_I_New:y_I_New+1);
                I_TF=I_Formula(X_I_k,Y_I_k);
                %然后是对结果的判断
                if xor(I_TF(1),I_TF(2))
                    Solve(y_I_New,x_I_New)=0;
                elseif I_TF(1)==true && I_TF(2)==true
                    Solve(y_I_New,x_I_New)=1;
                elseif I_TF(1)==false && I_TF(2)==false
                    Solve(y_I_New,x_I_New)=2;
                end
            else
                %如果是2，就跳过这个结果，因为确定不存在解
                Solve(y_I_New,x_I_New)=Solve_Old(y_I_Old,x_I_Old);
                continue
            end
            
        end
    end
    Solve_Old=Solve;
    %判断是否所有全部为2，如果是，则跳出
    if all(Solve==2)
        break
    end
    %绘图
    if k~=0
        %[X_Draw,Y_Draw]=meshgrid(0.5*(x(1:end-1)+x(2:end)),0.5*(y(1:end-1)+y(2:end)));
        figure(1)
        imagesc(0.5*(x(1:end-1)+x(2:end)),0.5*(y(1:end-1)+y(2:end)),Solve)
        set(gca,'YDir','normal')
        axis equal
        xlim(X);ylim(Y);
        colormap([[1,0,0];[0,0,0];[1,1,1]])%白色2的是背景，解为黑色1，不确定为红色0
        caxis([0,2])
        set(gcf,'Position',[440 10 800 800])
        pause(0.1)
    end
end
%将所有等于0的替换为1
Solve(Solve==0)=1;
%绘图
[X_Draw,Y_Draw]=meshgrid(0.5*(x(1:end-1)+x(2:end)),0.5*(y(1:end-1)+y(2:end)));
figure()
pcolor(X_Draw,Y_Draw,Solve)
shading flat



function I_TF=I_Formula(I_x,I_y)
% %示例等式1：y < x-2
% I_TF=Less(I_y,I_x-2);

% %示例等式2：y > x*x-1
% I_TF=Greater(I_y,I_Multi(I_x,I_x)-1);

%示例等式3：f(x,y) =cos(cos(min(sinx+y,x+siny))) − cos(sin(max(siny+x,y+sinx))) > 0
F1=I_Cos(I_Cos(I_Min( I_PLUS(I_Sin(I_x),I_y) , I_PLUS(I_Sin(I_y),I_x))));
F2=I_Cos(I_Sin(I_Max( I_PLUS(I_Sin(I_y),I_x) , I_PLUS(I_Sin(I_x),I_y))));
I_TF=Greater(F1,F2);

end

function I_Save=Mesh2Interval(x,y)
[x2,y2]=meshgrid(x,y);
I_Save=zeros((length(x)-1)*(length(y)-1),4);
k=1;
for kx=1:length(x)-1
    for ky=1:length(y)-1
        %储存为x1,x2,y1,y2的形式
        I_Save(k,:)=[x2(ky,kx),x2(ky,kx+1),y2(ky,kx),y2(ky+1,kx)];
        k=k+1;
    end
end
end

function Indxy=Mesh2IntervalInd(x,y)
Nx=length(x);
Ny=length(y);
Indxy=zeros((Nx-1)*(Ny-1),2);
k=1;
for kx=1:Nx-1
    for ky=1:Ny-1
        %储存为x1,x2,y1,y2的形式
        Indxy(k,:)=[kx,ky];
        k=k+1;
    end
end
end


function I_TF=Greater(I_A,I_B)
%区间算法，A>B
if I_A(1)>I_B(2)
    I_TF=[true,true];
elseif I_A(2)I_B(2)
    I_TF=[false,false];
elseif I_A(2)I_B(2)
    I_TF=[false,false];
else
    %两者存在交集
    I_TF=[false,true];
end
end


function I_C=I_PLUS(I_A,I_B)
%区间算法，A+B
I_C=[I_A(1)+I_B(1),I_A(2)+I_B(2)];
end

function I_C=I_MINUS(I_A,I_B)
%区间算法，A-B
I_B2=[-I_B(2),-I_B(1)];
I_C=I_PLUS(I_A,I_B2);
end

function I_C=I_Multi(I_A,I_B)
%区间算法，A*B
Multi_All=I_A'*I_B;
I_C=[min(min(Multi_All)),max(max(Multi_All))];
end

function I_C=I_Sin(I_A)
%区间算法，sin(x)
MinMax=[0,0];I_C=[0,0];
a=I_A(1);b=I_A(2);
%判断是否存在极大值
if floor((a/pi-0.5)/2)

3 其它展示

只是作为展示，遇到一些好玩的函数都会在这一节加更。
额外补充的函数以及定义域都会在后面注明。

3.1 展示1

用到的区间函数：

function I_C=I_Atan(I_A)
%区间算法 atan(A)，单调连续函数，所以直接区间变换就行
I_C=atan(I_A);
end

function I_C=I_Mod(I_A,b)
%区间算法，mod(A,b)，b是个常数，目前不支持区间
if ceil(I_A(1)/b)==ceil(I_A(2)/b)
    I_C=[mod(I_A(1),b),mod(I_A(2),b)];
else
    I_C=[0,b];
end
end

计算函数：

function I_TF=I_Formula(I_x,I_y)
%等式：mod(sqrt(x^2+y^2)-7/2*Arctan(x*y)+sin(x)*cos(y),pi)

定义域：[-30,30]
图片展示：

3.2 展示2

计算函数：

function I_TF=I_Formula(I_x,I_y)
%示例等式5：x/sin(x)+-y/sin(y)=+-x*y/sin(x+y)
F1=I_Divide(I_x,I_Sin(I_x));
F2=I_Divide(I_y,I_Sin(I_y));
F3=I_Divide( I_Multi(I_x,I_y),I_Sin(I_Multi(I_x,I_y)) );
I_TF1=Equal(I_PLUS(F1,F2) ,I_PLUS([-1e-3,-1e-3],F3) );
I_TF2=Equal(I_PLUS(F1,F2) ,I_MINUS([-1e-3,-1e-3],F3));
I_TF3=Equal(I_MINUS(F1,F2),I_MINUS([-1e-3,-1e-3],F3));
I_TF4=Equal(I_MINUS(F1,F2),I_PLUS([-1e-3,-1e-3],F3) );
if and(I_TF1(1),I_TF1(2))||and(I_TF2(1),I_TF2(2))||and(I_TF3(1),I_TF3(2))||and(I_TF4(1),I_TF4(2))
    I_TF=[true,true];
elseif xor(I_TF1(1),I_TF1(2))||xor(I_TF2(1),I_TF2(2))||xor(I_TF3(1),I_TF3(2))||xor(I_TF4(1),I_TF4(2))
    I_TF=[true,false];
else
    I_TF=[false,false];
end

定义域：[-10,10]
图片展示：

左边是我的图，右边是官方示例的图。发现我自己绘制的图多了很多不该出现的量，可以确定是因为除法在0附近的定义造成的。目前还不知道怎么消除这个影响。

不得不说，官方软件在很多细节上做的很好。