强化学习之Q-learning与Sarsa算法解决悬崖寻路问题
之前有写过利用Q-learning算法去解决->
一维二维探宝游戏：https://blog.csdn.net/MR_kdcon/article/details/109612413
有风格子寻路游戏：https://blog.csdn.net/MR_kdcon/article/details/110600819
理论与实践都证明：Q-learning对于解决状态有限、离散的RL任务有着不错的收敛效果。Q-learning是off-policy算法，意思是其行为策略与目标策略是独立的，根据这个特点，Agent就可以学习任意的行为策略，然后根据目标策略去优化策略。或者说有，由行为策略去探索环境，与环境沟通，沟通的结果喂给目标策略，但是其不决定目标策略的执行，这点很重要。因为TD算法的另一种叫on-policy算法，Sarsa是其典型代表，这种算法的行为策略和目标策略是同一个，意味着行为策略会直接决定目标策略的执行，故在选择行为策略的时候要小心一些。off-policy算法的另一个好处是，由于可以学习以往的经验、正在执行的经验、别人的经验，而Agent的探索是非常耗时间，通过直接用别人的经验就可以节省下自己去探索的时间，无疑是很有效率的一种方式。
我主要想通过这篇文章去描述Q-learning和Sarsa在RL任务中的一个特点：Q-learning对环境的探索比较大胆，而Sarsa对环境的探索就比较胆小、谨慎。
此外，TD算法对Q值的存储一般都是Q表（pandas表格）或者Q-字典：理论和实践都表明：Q字典完成RL的时间远远小于Q表，证明了Q字典在存储和搜索方面的优势。
实战内容：悬崖寻路
所需环境：pycharm
所需额外包：gym
一、实际效果：
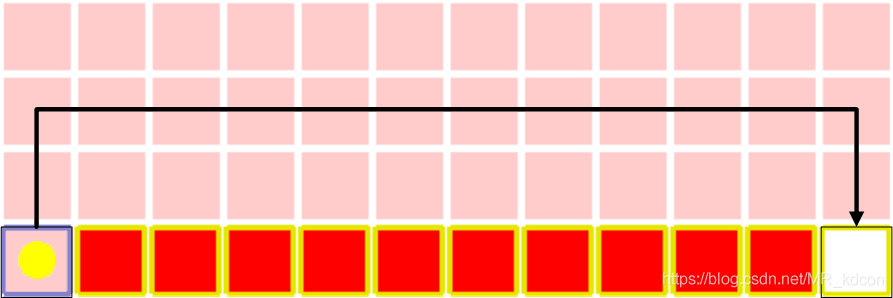
状态空间：4*12=48个位置索引。
动作空间 ：上下左右4个离散动作。
需要注意的是，右图中红色部分为“悬崖”，奖励为-100，共10个格子。最左边为起始点，最右边为终点，奖励为0，其余格子的奖励均为-1。
RL任务：Agent从起始点开始，寻找最优路径，避开悬崖，走到终点。（走入悬崖或者走到终点，都将返回到起点，开始新的episode）
1.1、Q-learning的实际效果：
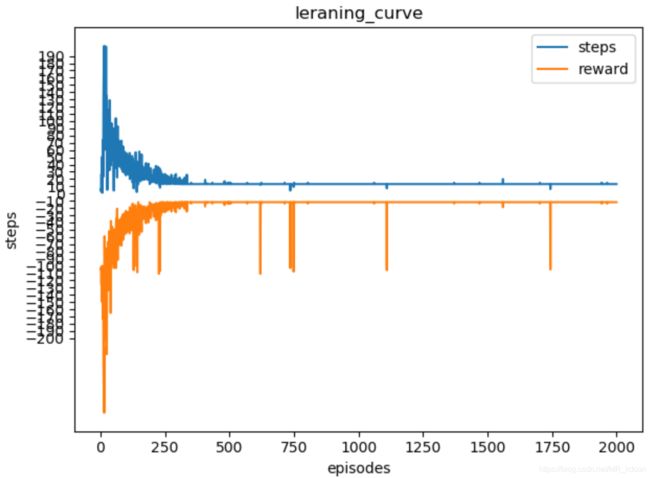
上左图是RL的学习曲线，可以看出大约350个episode之后，Agent开始找到了最优路径，到1000episode过程中会有瑕疵，是因为ε-greedy的ε参数并没有完全衰减到足够小，以至于会有随机动作的产生，到了900个episode之后，ε越来越靠近0，行为策略逐渐变成了目标策略，满足了收敛的GLIE条件。从另一个角度看，行为策略逐渐变成了确定性策略，那么就不会出现随机动作的情况，每一步的都是贪婪策略，其路径就是唯一的，即最优策略产生了。
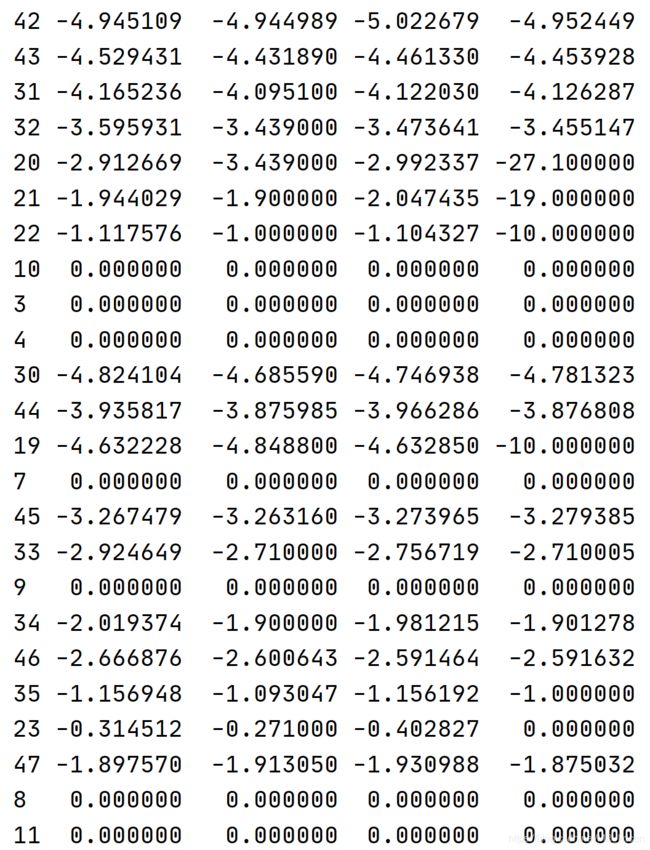
最右边2张图是达到收敛的Q表，从第12个状态（起点的上一格），可以看出，在贪心策略下，Q-learning必定会选择向右（0：左，1：右，2：上，3：下）。此外1000次的训练，一共972次是完整的episode。其余28次落入悬崖。
Note：从Q表中也可以看出，与理论符合，即离终点end越远的其Q值越小，因为Q值反映了该点执行动作a后的价值，其值在收敛后是接近Gt（带γ）的，若不考虑γ，比如状态0，向上，这个Q值应该是-12，但由于γ的原因以及算法是按α去接近（即有一定误差），就是表中的-7.18。纵观全表，Q值的分布和实际位置的Gt分布大致相符。如果你去计算衰减的Gt的话，你会发现它的值是接近Q值的，这也符合RL的理论，算是理论与实践相互验证了。
什么是GLIE条件呢？
GLIE条件（Greedy in the limit with the infinite exploration），即：
1、
：每个状态动作对都被无限次访问到，意味着采样次数多，那么Q和目标target就能无限接近。
2、
：策略最终趋向于贪婪策略，借鉴MDP中最优策略的产生是使用了纯贪婪策略，当探索到一定的时候，
最好为0以保持纯贪婪策略。
满足GILE条件，才能收敛至最优策略：
3、GLIE条件对MC、TD算法都适用。
上右图是收敛之后，Agent的最优路径需要花13步，总奖励为-12。如下图所示：
1.2、Sarsa的实际效果：
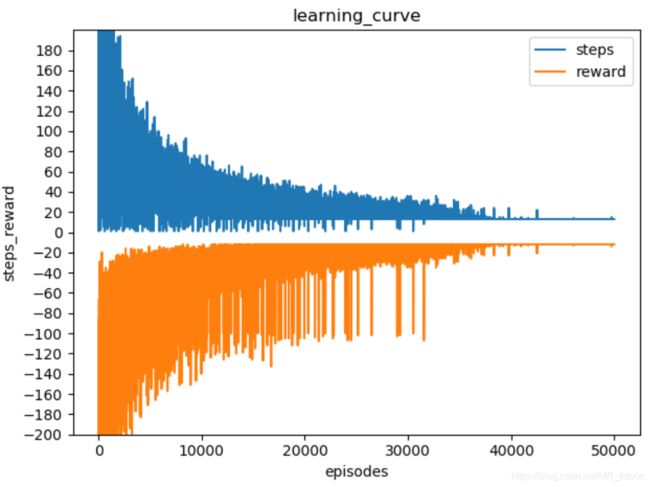
上左图是是Sarsa算法的学习曲线，其最后收敛的最优路径步数竟然是15！，可是Q-learning不是做出来13吗？那么Sarsa怎么走的呢？
如上图所示，这是Sarsa最后收敛的最优路径。显然这个最优路径是假的，因为明显有比他更好的，但算法角度来看，这确实是Sarsa的最优路径，因为其符合GLIE条件。
最右边2张图是达到收敛的Q表，从第12个状态（起点的上一格），可以看出，在贪心策略下，Q-learning必定会选择向上（0：左，1：右，2：上，3：下）。此外1000次的训练，一共970次是完整的episode。其余30次落入悬崖。
二、Q-learning和Sarsa算法：
2.1、伪代码（左Q右Sarsa）：
从上述代码中我们可以得出Sarsa月Q-learning的不同之处：
1、Sarsa产生的A'在优化完成后的下一步一定也会被执行，而Q-learning用于更新Q表的A'在下一个step不一定会被执行，因此执行策略是-greedy策略，可能会产生随机动作。
2、Sarsa用同一个策略产生了样本
2.2、学习曲线（左Q右Sarsa）：
对比上面2张图：Q-learning要270个episode才找到最优路径，而Sarsa要570个episode才找到，说明Q-learning收敛速度更快。
对于学习率，之前在https://blog.csdn.net/MR_kdcon/article/details/110600819有提到过，在RL中，学习率较大，有利于收敛速度的加快，为了更明显体现，这里采用alpha=0.1、0.01、0.001来分析，为保证效率，采用Q字典为Q值的存储方式。
由于Q-learning的方差较小，故选择Q-learning算法来测试：
对于α=0.1：
对于α=0.01：
对于α=0.001：
从上面对比可看出，
0.1的学习率，Agent在400个epoch就可以基本收敛，形成成熟的Q表。
0.01的学习率，Agent在3400个epoch就可以基本收敛，形成成熟的Q表。
0.001的学习率，Agent在40000个epoch就可以基本收敛，形成成熟的Q表。
0.001的学习率似的Q估计值靠近TD目标值的速度很慢，换句话说，TD目标值靠近Q真值的速度也很慢，从而形成成熟的Q值也很慢，即很慢才收敛。α=0.001的时候，在5000的epoch之后，Agent其实一直在逛来逛去，最后才到达终点，意味着Agent并没有找到最佳路径，而那时候ε其实已经很小了，行为策略几乎就是贪心策略，那么解释这个现象的原因就是：形成最优策略的Q(s,a)没有在同一个状态下的其余Q值中成为最大值，第二个原因是Q(s,a)不够准确，而导致这个的原因就是Q估计值接近TD目标值太慢了，TD目标值接近Q真实值太慢了，所以Q估计值接近Q真实值就很慢（Q(s,a)真实值就是在策略π下，在状态s，执行动作a后，能获取的真实Gt值的估计），这就是不够准确，而且Q真实值中也包括了那个最大值的Q(s,a)，这个值的形成同样也很慢才到达真实值，这就是还未成为最大值，需要注意的是，最终在Q(s)中最大的值叫最优值函数，这个最优值函数虽然最后成为了老大，但是在最初初始化开始到最终形成的过程中，其值不一定是一直是老大，甚至有一段时间，还是最小，这是为什么呢？
举个例子，如下图所示：
为了便于分析，我们忽略那个以α速度靠近的过程，选择直接靠近。那么Q(s')的估计值就如图所示，其中Q(S',向下)是最优值函数。从s'的值函数中也可以看出，最优值函数是如何形成的。那么对于最优值函数不一定从头到尾都是同状态下的最大值这个问题呢，得看状态s时，我们初始化下Q(s,a)都是0，但是当我们在S的时候，由于行为策略的随机性，我们选择了向下，因此Q(s,向下)=-α
2.3、造成Sarsa偏离最优策略的原因：
对于第一点，很好理解，对于第二点，更加深入的去分析：
分析：
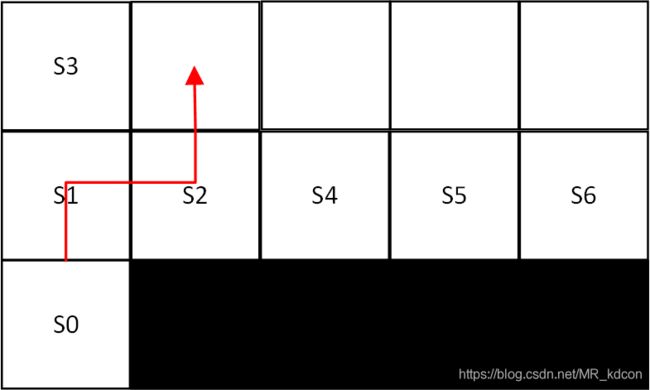
如上图所示，我截取了前面几个状态来分析Sarsa和Q-learning在选择路径上的不同之处。（α=-0.5，
=1）
首先对于Sarsa：
如上图伪代码所示：
1、在S0时，根据 -greedy策略，若选择a=向上，获得s'=S1,R=-1,根据-greedy策略，若在s'=S1处选择a'=向右，更新Q(S0,向上)=0+1/2*(-1+0-0)=-0.5，s=S1，a=向右。来到S1。
2、获得s'=S2,R=-1,根据-greedy策略，若选择a'=向下，更新Q(S1,向右)=0+1/2*（-1+0-0）=-0.5，s=S2，a=向下，来到S2。
3、获得s'=end，R=-100，更新Q(S2,向下)=0+1/2*（-100+0-0）=-50，s=end，重新启动。
4、在S0时，根据 -greedy策略，选择a=向上，获得s'=S1,R=-1,根据-greedy策略，在s'=S1处选择a'=向右，更新Q(S0,向上)=-0.5+1/2*（-1-0.5+0.5）=-1，s=S1，a=向右，来到S1。
5、获得s'=S2,R=-1,根据-greedy策略，选择a'=向下，更新Q(S1,向右)=-0.5+1/2*（-1-50+0.5）=-25.75。
。。。
换一种探索方式：
6、在S0时，根据 -greedy策略，选择a=向上，获得s'=S1,R=-1,根据-greedy策略，若在s'=S1处选择a'=向上，更新Q(S0,向上)=-1+1/2*（-1+0+1）=-1，s=S1，a=向上，来到S1。
7、获得s'=S3,R=-1,根据-greedy策略，选择a'=向上，更新Q(S1,向上)=0+1/2*（-1+0-0）=-0.5，s=S3，a=向上，来到S3。（对比2中，此时S1不管-greedy策略中选用随机策略还是贪心策略，2种方向都能被选择。但是对比5，此时若使用-greedy策略中的贪心策略，则Agent会避开S2，选择S3，即避开悬崖。由于贪心策略被采样的概率较大，因此绝大部分情况，Sarsa都会避开和悬崖相邻的那一排）
其次对于Q-learning：
1、S0，根据-greedy策略，a=向上，获得s'=S1，R=-1，根据greedy策略，Q(S0,向上)=0+1/2*(-1+0-0)=-0.5。s=S1，来到S1。
2、根据-greedy策略，a=向右，获得s'=S2，R=-1，根据贪心策略，Q(S1,向右)=0+1/2*(-1+0-0)=-0.5。s=S2，来到S2。
3、根据-greedy策略，a=向下，获得s'=end，R=-100，根据贪心策略，Q(S2,向下)=0+1/2*(-100+0-0)=-50。s=end，重新启动。
4、S0，根据-greedy策略，a=向上，获得s'=S1，R=-1，根据greedy策略，Q(S0,向上)=-0.5+1/2*(-1+0+0.5)=-0.75。s=S1，来到S1。
5、根据-greedy策略，a=向右，获得s'=S2，R=-1，根据贪心策略，Q(S1,向右)=-0.5+1/2*(-1+0+0.5)=-0.75。s=S2，来到S2。
换一种探索方式：
6、S0，根据-greedy策略，a=向上，获得s'=S1，R=-1，根据greedy策略，Q(S0,向上)=-0.5+1/2*(-1+0+0.5)=-0.75。s=S1，来到S1。
7、根据-greedy策略，a=向上，获得s'=S3，R=-1，根据贪心策略，Q(S1,向上)=0+1/2*(-1+0-0)=-0.5。s=S3，来到S3。
.。。。重新启动
8、S0，根据-greedy策略，a=向上，获得s'=S1，R=-1，根据greedy策略，Q(S0,向上)=-0.75+1/2*(-1+0+0.75)=-7/8。s=S1，来到S1。
9、根据-greedy策略，a=向上，获得s'=S3，R=-1，根据贪心策略，Q(S1,向上)=-0.5+1/2*(-1+0+0.5)=-0.75。s=S3，来到S3。（对比5中，S1处此时不管-greedy策略是均一策略还是贪心策略，Agent都有可能去选择向右行走，不畏惧悬崖边）
从上面段分析我们可以得出：
1、Q-learning，在已知Q(S2,向下)很小的情况下，在S1时，若选到了向右动作a（行为policy），和环境交互产生s'和R，然后目标policy将根据s'产生具有最大动作值函数对应的动作a'，而a与a‘来自于2个不同的策略，即目标policy和行为policy独立，Q(S2,向下)这个糟糕的值（很小）一定不会影响到Q(S1,向右)。
2、而Sarsa，在已知Q(S2,向下)很小的情况下，在S1时，执行向右(行为policy)，由于行为policy和目标policy是一体的，若接下来行为ε-policy在S2选中向下，则目标policy跟着完蛋，即行为策略要是不好，会直接导致目标策略不好，从而使得值函数的评估出现问题（比如此时Q(S2,向下)会直接影响到Q(S1,向右)大幅下降。Q(S1,向右)大幅下降，直接导致了Q(S1,向上)>Q(S1,向右)，因此只有在-greedy策略为均一策略的时候，Agent才会走到S2状态上去，其余情况都往S3走，从而错失了最优路径）。接下来Agent就会走到S2，并执行向下的动作。
3、同理，对于后续情况，Sarsa还是会采取避开悬崖边的方案。
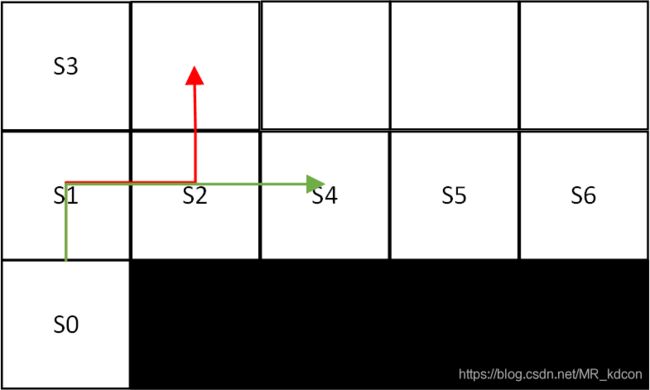
4、还有一个调试经验就是：当探索率ε越小的时候，在S1往右走的概率越大，就是说当ε较大的时候，在S1很大概率都往上走，避开最优路线，原因就在于“上面分析的第五条粉红色加粗部分”，ε较大的时候，随机探索比较强，因此进入S2下面这个陷阱概率就很大，更糟糕的事，一旦进入过一次，那么Q(s1,向右)就会变的很小，那么自然之后在S1就会往上走了，这就是我们上面分析的情况。那么我们现在在讨论ε比较小的时候，比如0.001-0.01，这时候粉红色加粗部分会大概率选择a'=向上或向右，这是贪心策略在其作用，那么这时候Q(s1,向右)就不会很小了，而是正常探索的值。因此就会出现说agent最终策略会在S1向右走的可能。那么有没有可能在S2继续往右走呢？也是可能的，但发生概率比在S2向上走要小，而且越贴着悬崖往右走的概率越小。因为我们不妨设S2往右走的状态是S4（S3上面已经用过了）。那么同理，但凡在S4往下走入过悬崖一次，那么之后Q(s2,向右)的值就会很小（这和上述在S1的分析同理），他会就选择向上走，如下图所示：
这里的关键是只要走下去过一次，那么你就不可能继续贴着走，而Sarsa中的行为策略是随机策略，不可能说一次都不掉下悬崖。
因此我们说红色、绿色都有可能发生，但是相对而言，红色发生概率更大。
那么继续分析，如果来到了S4，那么同理，红色线概率更大，因为你还得保证在S5一次都不能掉下去，这太难了，你已经在S4保证一次都不掉下去的情况下，ε虽然小但是不等于0，这是候你还得保证S5一次都不犯错，这基本上不可能了，实践也表明，最多在S5还贴着悬崖，然后就不会继续往右了。
总结：
①：ε越小，继续贴着悬崖走的概率越大。
②：贴着悬崖格数越少的最终路径出现概率越大。
③：Sarsa寻找最优路径（贴悬崖走是最优路径）的容错率很小，只要走入一次，接下去基本与最优路径无缘了。比如Q(s1,向上)=-0.5，Q(s1,向右)=-25，经测试，该状态的Q真实值差不多在-7.5左右，那么TD算法的软更新告诉我们，Q(s1,向右)之后确实会接近真实值，但是Q(s1,向上)更容易接近这个真实值，因此最终在贪心策略下，S1只会选择向上。这种容错率告诉我们，Sarsa算法对探索的严格程度远远高于Q-learning。
④：但至于说一旦选择上述红色线后，为啥会向右，而不是继续向上。这是因为一旦想上之后，就和我们平时寻优情况一样了，就是按最短路径来，显然向右的路径更短。
三、总结：
3.1、Q-learning大胆而Sarsa胆小的原因：
对Sarsa，当处于S1，动作A向右的时候，行为策略ε-greedy策略会有一定几率在S2选到向下的动作，关键来了，在下一步的时候，会转移到S2，且会执行向下的动作，然后下一步Agent就会落入悬崖，且会导致Q(s2,向下)的值变得贼小，这个Q值的变小直接导致了Q(s1,向右)一般会变得很小，这样下次在S1的时候，Agent就会大概率不往右走了，也就是说处于S1的时候，不会往右走。
对Q-learning，当处在S1，动作A向右的时候，Q(s2,向下)这个很小的值不会影响Q(S1,向右)，这样下次在S1的时候，Agent还是会大概率向右走，这不是比Sarsa更加大胆了。且当下一步转移到S2的时候，Agent又会执行ε-greedy策略，而这个策略又会产生新的动作，大概率不会向下，因此Q-learning显得更加肆无忌惮一些，哪怕小概率中奖了，选到了向下也没事，大概率还是可以继续探索的（即选到其他动作）。
3.2、Q-learning可以学别人而Sarsa不可以的原因：
1、一般我们喂给算法的是trans，即
根据Sarsa，Q更新的a'是根据行为策略得到，若行为策略随机到了向下，Q更新的a'是根据行为策略得到的，故Q的更新就会受到这个行为策略的影响，Q(s2,向下)这个很小的值就会让Q(s1,向右)的值变得很小，这样就会使Agent避开悬崖边而选择向上走。因此trans的提供需要小心选择，不然容易造成上面的局面。提供trans的过程其实就是探索的过程，Sarsa这种不能接受任意trans的能力意味着其探索能力有限。
根据Q-learning，Q更新的a'是根据目标策略得到的，因此其Q的更新并不受Q(s2,向下)的影响，或者说在S2不会选择向下的动作，那么Q(s1,向右)的值不会很小（而且贪心策略还会增加这个值，向着最优值函数靠近），那么下次在S1的时候，就不会避开悬崖边的格子了。因此trans的提供可以任意提供，并且直接更新Q，可以省去了与环境的探索，事实上，与环境探索，产生样本的过程是最耗时间的，这无疑增加了效率。提供trans的过程其实就是探索的过程，Q-learning这种接受任意trans的能力意味着其探索能力的强大。
2、根据3.1，Q-learning的探索能力更强，因为其大胆。而Sarsa的探索能力有限，比如根据行为策略，在S1大概率只能向上，因此其会损失很多很有潜力的状态（比如悬崖边的那些状态其实是最好的状态），这点我们从结果也可以看出，Sarsa从算法层面选出的最优路径并不是真实的最优路径，说明其对环境的理解不够充分。他其实并没有求出悬崖边状态的真实价值。