leetcode 15. 三数之和

---

排序+双指针

解题思路：

• 暴力法搜索为 O(N^3)时间复杂度，可通过双指针动态消去无效解来优化效率。
• 双指针法铺垫： 先将给定 nums 排序，复杂度为 O(NlogN)。
• 双指针法思路：
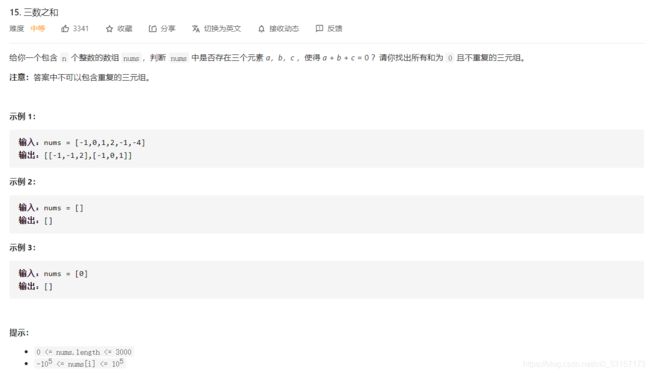
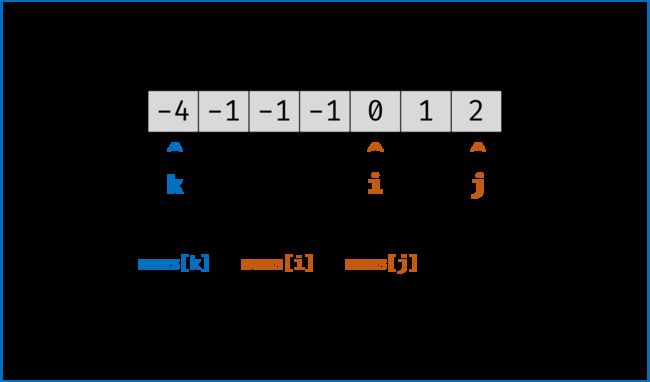
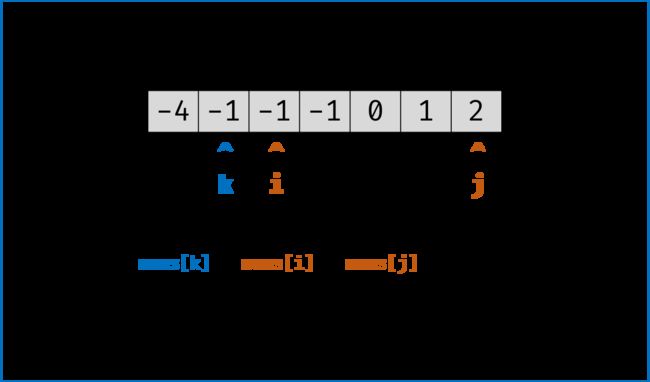
  1.定义三个指针k,p,q ,固定 3 个指针中最左（最小）数字的指针 k
  2.k指针指向数组中第一个元素，p指针最开始指向k前面一个元素，q指针最开始指向数组最后一个元素
  3.通过双指针交替向中间移动，记录对于每个固定指针 k 的所有满足 nums[k] + nums[i] + nums[j] == 0 的 i,j 组合：

1.当 nums[k] > 0 时直接break跳出：因为 nums[j] >= nums[i] >= nums[k] > 0，即 3 个数字都大于 0，在此固定指针 k 之后不可能再找到结果了。
2.当 k > 0且nums[k] == nums[k - 1]时即跳过此元素nums[k]：因为已经将 nums[k - 1] 的所有组合加入到结果中，本次双指针搜索只会得到重复组合。
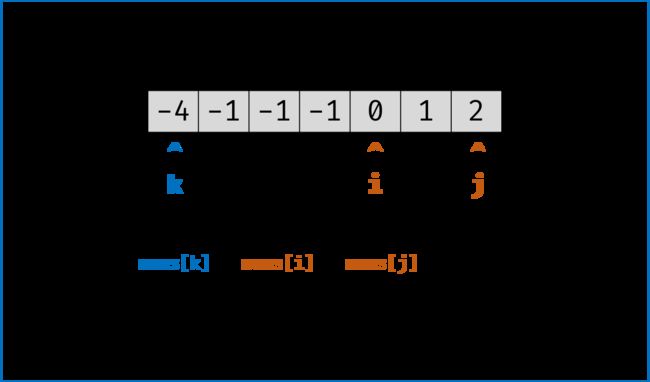
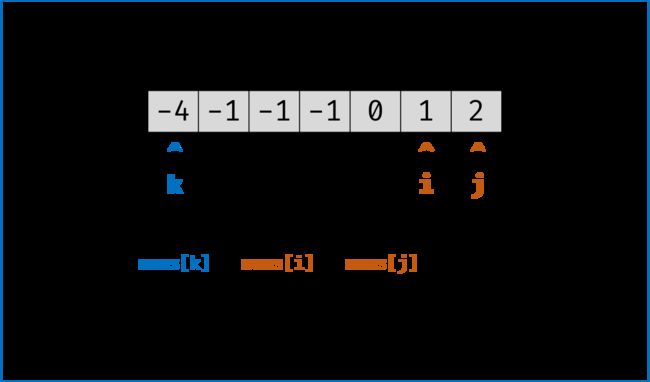
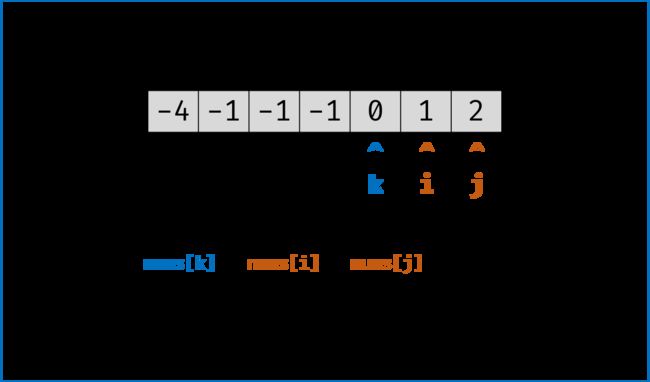
3. i，j 分设在数组索引 (k, len(nums))两端，当i < j时循环计算s = nums[k] + nums[i] + nums[j]，并按照以下规则执行双指针移动：
(1) 当s < 0时，i + = 1并跳过所有重复的nums[i]；
(2) 当s > 0时，j - = 1并跳过所有重复的nums[j]；
(3) 当s == 0时，记录组合[k, i, j]至res，执行i += 1和j -= 1并跳过所有重复的nums[i]和nums[j]，防止记录到重复组合。

复杂度分析：

• 时间复杂度 O(N^2)：其中固定指针k循环复杂度 O(N)，双指针 i，j 复杂度 O(N)。
• 空间复杂度 O(1)：指针使用常数大小的额外空间。

图解：

注意：这里要固定一个最左的指针K，可以理解为从[i,j]范围里面选出两个值相加为K指针指向值的相反数
K每次往后移动一次，[i,j]范围都会缩小一个单元
代码:

class Solution {
     
public:
	vector<vector<int>> threeSum(vector<int>& nums) 
	{
     
		//获取当前数组的长度
		int size = nums.size();
		//构造存储所有结果的数组
		vector<vector<int>> ret;
		//如果当前数组长度小于3，直接返回空容器
		if (size < 3) return ret;
		//给数组排序
		sort(nums.begin(), nums.end());
		//固定k指针不断后移,[p,q]寻找范围不断缩小
		for (int k = 0; k < size; k++)
		{
     
			if (nums[k] > 0) return ret;//数组中最小的数都大于0
			if (k > 0 && nums[k] == nums[k - 1]) continue;//当前存在重复元素，如果算入可能会出现重复解
			int p = k + 1, q = size - 1;//前后两个指针
			while (p < q)//当前指针位于后指针
			{
     
				int sum = nums[k] + nums[p] + nums[q];
				if (sum < 0)//说明当前的总和小了，我们需要增大相加的总和----前指针后移
					while (p < q && nums[p] == nums[++p]);//如果前指针后移出现重复数字就一直后移，直到没有出现重复元素为止，否则只移动一次
				else if (sum > 0)//说明当前的总和大了，我们需要减小相加的总和----后指针前移
					while (p < q && nums[q] == nums[--q]);//同上，不重复就只移动一次
				else//sum=0,满足题目要求
				{
     
					ret.push_back({
      nums[k],nums[p],nums[q] });//当前结果导入数字
					//前指针后移，后指针前移继续寻找当前固定k值下的可能解
					//同上，没有出现重复解，移动一次
					while (p < q && nums[p] == nums[++p]);
					while (p < q && nums[q] == nums[--q]);
				}
			}
		}
		return ret;
	}
};	

---

哈希法

我们这个题目的哈希表解法是很容易理解的，我们首先将数组排序，排序之后我们将排序过的元素存入哈希表中，我们首先通过两层遍历，确定好前两位数字，那么我们只需要哈希表是否存在符合情况的第三位数字即可，跟暴力解法的思路类似，很容易理解，但是这里我们需要注意的情况就是，例如我们的例子为[-2 , 1 , 1],如果我们完全按照以上思路来的话，则会出现两个解，[-2 , 1 , 1]和[1 , 1, -2]。具体原因，确定 -2，1之后发现 1 在哈希表中，存入。确定 1 ，1 之后发现 -2 在哈希表中，存入。所以我们需要加入一个约束避免这种情况，那就是我们第三个数的索引大于第二个数时才存入。

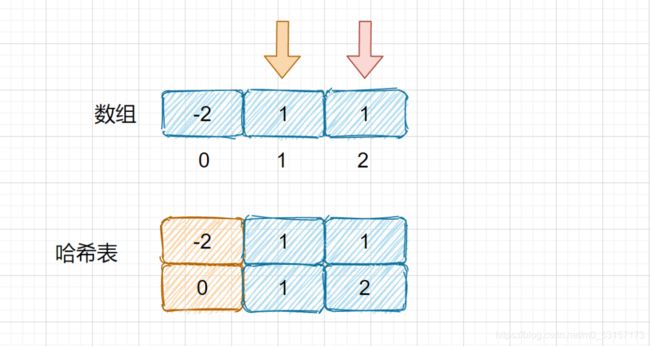
上面这种情况时是不可以存入的，因为我们虽然在哈希表中找到了符合要求的值，但是 -2 的索引为 0 小于 2 所以不可以存入。

class Solution {
     
public:
	vector<vector<int>> threeSum(vector<int>& nums) 
	{
     
		//获取当前数组的长度
		int size = nums.size();
		//构造存储所有结果的数组
		vector<vector<int>> ret;
		//如果当前数组长度小于3，直接返回空容器
		if (size < 3) return ret;
		//给数组排序
		sort(nums.begin(), nums.end());
		//哈希容器---关键字是对应元素的值，值是下标
		map<int, int> m;
		for (int i = 0; i < size; ++i)
			m[nums[i]] =i;

		for (int k = 0; k < size-2; k++)
		{
     
			if (nums[k] > 0) return ret;//排序之后如果第一个元素已经大于零，那么不可能凑成三元组
			//对元素a去重
			if (k>0&&nums[k] == nums[k-1]) continue;
			for (int j = k + 1; j < nums.size(); j++) {
     
				if (j>k+1&&nums[j] == nums[j-1]) continue;//对元素b去重
				int c = -(nums[k] + nums[j]);
				//当前数组中存在元素c,并且元素c下标大于元素b的下标
				if (m.find(c) != m.end())
				{
     
					if (m[c] > j)
						ret.push_back({
      nums[k],nums[j],c });
					else
						break;//首先当前已经不存在满足条件的元素c了，在往数组后面寻找元素b，b越大，需要的c越小，更不可能满足条件
				}
			}
		}
		return ret;
	}
};