python画正太分布曲线图细高_判断一组数据是否来自正态分布
第九题 2020年11月29日
第九题 2020年11月29日
方法一 概率密度曲线比较法
比较样本与正态分布概率密度曲线的拟合程度,R代码如下:
set.seed(2020)
# 画样本概率密度图
s 100) #产生样本
d plot(d, col="green", ylim=c(0, 0.5))
# 添加正态分布概率密度图
s2 4, to=4, length.out=100)
lines(s2, dnorm(s2), col="red")

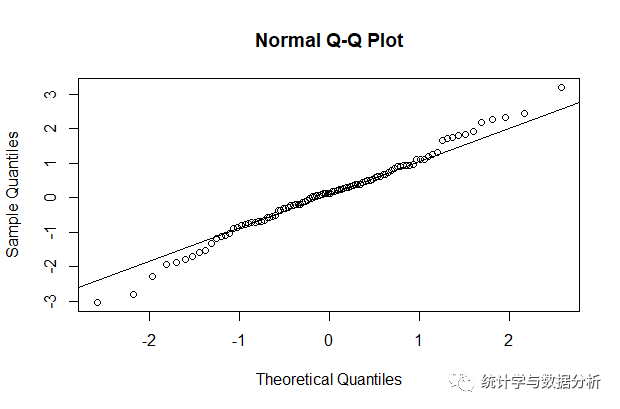
方法二 正态Q-Q图法
使用Q-Q图来判断数据是否服从正太分布,R代码如下:
set.seed(2020)
s 100) # 产生样本
qqnorm(s)
qqline(s)
方法三 经验法则
约68.3%数值分布在距离平均值有1个标准差之内的范围,约95.4%数值分布在距离平均值有2个标准差之内的范围,以及约99.7%数值分布在距离平均值有3个标准差之内的范围。称为“68-95-99.7法则”或“经验法则”。
set.seed(2020)
s 10000) # 产生样本
sum(abs(s - mean(s)) sum(abs(s - mean(s)) 2*sd(s)) / length(s)
sum(abs(s - mean(s)) 3*sd(s)) / length(s)
方法四 统计检验方法
可以使用夏皮罗-威尔克(Shapiro-Wilk)检验,代码如下:
s 1000) # 产生样本
shapiro.test(s)
shapiro.test函数输出一个p值,照惯例,p<0.05说明总体不太可能是正态分布,否则不能提供这么个证据,也就是说这个检验比较保守,倾向于错误的过分证明正态性。
详细的介绍可以参见:Statistical Analysis Handbook 2018 edition,by Dr Michael J de Smith (Author)。
更多的统计检验方法可见该书的第十二章经典检验,电子版链接为:http://www.statsref.com/HTML/index.html?shapiro_wilk.html
其他
如果需要,可以进一步采取下面的两个包:
1、nortest包 lillie.test()可以实行更精确的Kolmogorov-Smirnov检验。ad.test()进行Anderson-Darling正态性检验。cvm.test()进行Cramer-von Mises正态性检验。pearson.test()进行Pearson卡方正态性检验。sf.test()进行Shapiro-Francia正态性检验。
2、fBasics包 normalTest()进行Kolmogorov-Smirnov正态性检验。ksnormTest()进行Kolmogorov-Smirnov正态性检验。shapiroTest()进行Shapiro-Wilk's正态检验。jarqueberaTest()进行jarque-Bera正态性检验。dagoTest进行D'Agostino正态性检验。gofnorm采用13种方法进行检验,并输出结果。
分布检验方法比较
图示法相对于其他方法而言,比较直观,方法简单,从图中可以直接判断,无需计算,但这种方法效率不是很高,它所提供的信息只是正态性检验的重要补充。
经常使用的拟合优度检验和Kolmogorov-Smirnov检验的检验功效较低,在许多计算机软件的Kolmogorov-Smirnov检验无论是大小样本都用大样本近似的公式,很不精准,一般使用Shapiro-Wilk检验和Lilliefor检验。
Kolmogorov-Smirnov检验只能检验是否一个样本来自于一个已知样本,而Lilliefor检验可以检验是否来自未知总体。
Shapiro-Wilk检验和Lilliefor检验都是进行大小排序后得到的,所以易受异常值的影响。
Shapiro-Wilk检验只适用于小样本场合(3≤n≤50),其他方法的检验功效一般随样本容量的增大而增大。
拟合优度检验和Kolmogorov-Smirnov检验都采用实际频数和期望频数进行检验,前者既可用于连续总体,又可用于离散总体,而Kolmogorov-Smirnov检验只适用于连续和定量数据。
拟合优度检验的检验结果依赖于分组,而其他方法的检验结果与区间划分无关。
偏度和峰度检验易受异常值的影响,检验功效就会降低。
假设检验的目的是拒绝原假设,当p值不是很大时,应根据数据背景再作讨论。