Eigen库使用指南(转载)
Eigen库使用指南(转载)
目录
Eigen库使用指南(转载)
1.模块和头文件
2. Matrix类
3. 矩阵与向量的运算
4. Array类
5. 块操作
6. 矩阵初始化
7. 归约,迭代器,广播
8. Map类
9. 混淆问题
1.模块和头文件
Core#include,包含Matrix和Array类,基础的线性代数运算和数组操作。Geometry#include,包含旋转,平移,缩放,2维和3维的各种变换。LU#include,包含求逆,行列式,LU分解。Cholesky#include,包含LLT和LDLT Cholesky分解。SVD`#include,包含SVD分解。 QR`#include,包含QR分解。 Eigenvalues#include,包含特征值,特征向量分解。Sparse#include,包含稀疏矩阵的存储和运算。Dense#include,包含了Core/Geometry/LU/Cholesky/SVD/QR/Eigenvalues模块。Eigen#include,包含Dense和Sparse。
2. Matrix类
- 所有矩阵和向量都是
Matrix模板类的对象,Matrix类有6个模板参数,主要使用前三个,剩下的使用默认值。
Matrix
# Scalar 元素类型
# RowsAtCompileTime 行
# ColsAtCompileTime 列
# 例 typedef Matrix Matrix3i;
# Options 比特标志位
# MaxRowsAtCompileTime和MaxColsAtCompileTime表示在编译阶段矩阵的上限。
# 列向量
typedef Matrix Vector3d;
# 行向量
typedef Matrix RowVector3f;
# 动态大小
typedef Matrix MatrixXd;
typedef Matrix VectorXf;
- 默认构造时,指定大小的矩阵,只分配相应大小的空间,不进行初始化。动态大小的矩阵,则未分配空间。
[]操作符可以用于向量元素的获取,但不能用于matrix。Eigen支持以下的读/写元素语法:
matrix(i,j);
vector(i)
vector[i]
vector.x() // first coefficient
vector.y() // second coefficient
vector.z() // third coefficient
vector.w() // fourth coefficientmatrix的大小可以通过rows(),cols(),size()获取,resize()可以重新调整矩阵大小。- 上述的元素访问方法都通过断言检查范围,代价比较大。
- 通过定义EIGEN_NO_DEBUG 或 NDEBUG,取消断言。
- 通过使用coeff()和coeffRef(),来取消检查。比如,MatrixBase::coeff(int,int) const, MatrixBase::coeffRef(int,int)等。
3. 矩阵与向量的运算
- Eigen不支持类型自动转化,因此矩阵元素类型必须相同。
- 支持
+, -, +=, -=, *, /, *=, /=基础四则运算。 - 转置和共轭
MatrixXcf a = MatrixXcf::Random(3,3);
a.transpose(); # 转置
a.conjugate(); # 共轭
a.adjoint(); # 共轭转置(伴随矩阵)
# 对于实数矩阵,conjugate不执行任何操作,adjoint等价于transpose
a.transposeInPlace() #原地转置
Vector3d v(1,2,3);
Vector3d w(4,5,6);
v.dot(w); # 点积
v.cross(w); # 叉积
Matrix2d a;
a << 1, 2, 3, 4;
a.sum(); # 所有元素求和
a.prod(); # 所有元素乘积
a.mean(); # 所有元素求平均
a.minCoeff(); # 所有元素中最小元素
a.maxCoeff(); # 所有元素中最大元素
a.trace(); # 迹,对角元素的和
# minCoeff和maxCoeff还可以返回结果元素的位置信息
int i, j;
a.minCoeff(&i, &j);4. Array类
Array是个类模板,前三个参数必须指定,后三个参数可选。
Array
# 常见类定义
typedef Array ArrayXf
typedef Array Array3f
typedef Array ArrayXXd
typedef Array Array33d
ArrayXf a = ArrayXf::Random(5);
a.abs(); # 绝对值
a.sqrt(); # 平方根
a.min(a.abs().sqrt()); # 两个array相应元素的最小值 - 当执行array*array时,执行的是相应元素的乘积,所以两个array必须具有相同的尺寸。
Matrix对象——>Array对象:.array()函数Array对象——>Matrix对象:.matrix()函数
5. 块操作
块是matrix或array中的矩形子块。
// 方法1
.block(i, j, p, q) //起点(i, j),块大小(p, q),构建一个动态尺寸的block
.block(i, j) // 构建一个固定尺寸的block matrix.row(i): 矩阵第i行matrix.col(j): 矩阵第j列
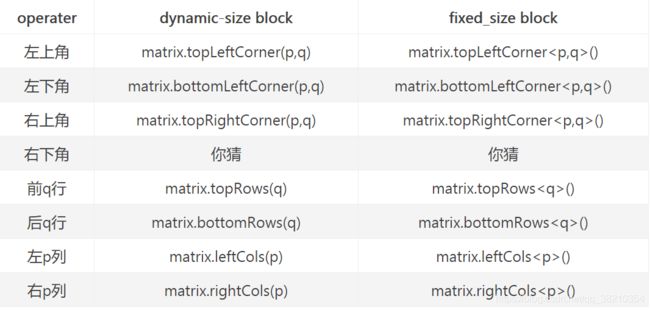
- 角相关操作
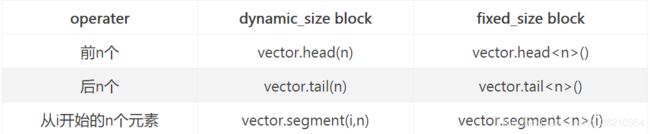
Vector的块操作
6. 矩阵初始化
- 逗号初始化:为矩阵元素赋值,顺序是从左到右,从上到下,数目必须匹配。
// 初始化列表除数字外也可以是vectors或matrix
RowVectorXd vec1(3);
vec1 << 1,2,3;
RowVectorXd vec2(2);
vec2 << 4,5;
RowVectorXd vec3(5);
vec3 << vec1, vec2;
// 也可以使用block结构初始化
- 特殊矩阵
- 零阵:类静态成员函数
Zero() - 常量矩阵:
Constant(rows, cols, value) - 随机矩阵:
Random() - 单位矩阵:
Identity()
- 零阵:类静态成员函数
LinSpaced(size, low, high):构建从low到high等间距的size长度的序列,适用于vector和一维数组。- 功能函数
- `setZero()
setIdentity()
7. 归约,迭代器,广播
- 范数计算
squareNorm():L2范数,等价于计算vector自身点积norm():返回`squareNorm的开方根.lpNorm:p范数,p可以取()
Infinity,表无穷范数
- 布尔归约
all()=true: matrix或array中所有元素为trueany()=true: 到少有一个为truecount(): 返回true元素个数
// sample
ArrayXXf A(2, 2);
A << 1,2,3,4;
(A > 0).all();
(A > 0).any();
(A > 0).count();
- 迭代器,获取某元素位置
// sample
Eigen::MatrixXf m(2,2);
m << 1,2,3,4;
MatrixXf::Index maxRow, maxCol;
float max = m.maxCoeff(&minRow, &minCol);
- 部分归约,
// sample
Eigen::MatrixXf mat(2,3);
mat << 1,2,3,
4,5,6;
std::cout << mat.colwise().maxCoeff();
// output: 4, 5, 6
// mat.rowWise() the same as before
- 广播,针对vector,沿行或列重复构建一个matrix。
// sample
Eigen::MatrixXf mat(2,3);
Eigen::VectorXf v(2);
mat << 1,2,3,4,5,6;
v << 0,1;
mat.colwise() += v;
// output: 1, 2, 3, 5, 6, 78. Map类
- Map类用于利用数据的内在,并将其转为Eigen类型。
- 定义:
Map > -
通过Map来reshape矩阵的形状。
9. 混淆问题
- 使用
eval()函数解决把右值赋值为一个临时矩阵,再赋给左值时可能有造成的混淆。如:
MatrixXi mat(3,3);
mat << 1,2,3, 4,5,6, 7,8,9;
mat.bottomRightCorner(2,2) = mat.topLeftCorner(2,2).eval();
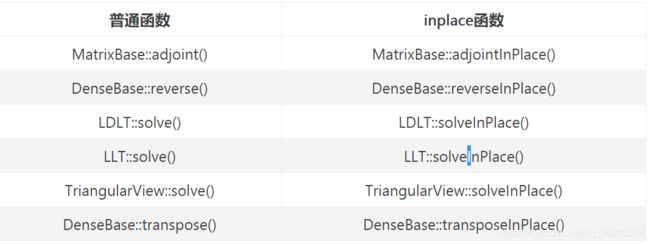
- 原地操作的一类函数:
- 当相同的矩阵或array出现在等式左右时,容易出现混淆
- 当确定不会出现混淆时,可以使用
noalias() - 混淆出现时,可以使用
eval()和xxxInPlace()函数解决
作者:zhaoQiang012
链接:https://www.jianshu.com/p/931dff3b1b21
来源:简书
更多请参考:https://blog.csdn.net/xuezhisdc/article/details/54619853