详解活动图计算关键路径、最早开始时间、最晚开始时间、冗余时间，C++ 程序实现

题目

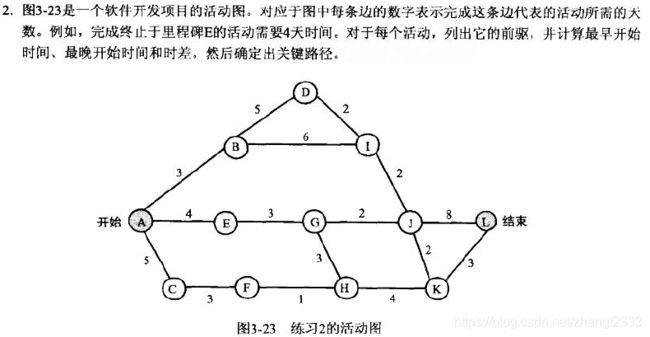
下图是一个软件开发项目的活动图，对于图中每条边的数字表示完成这条边代表的活动的天数。例如，完成终止于里程碑E的活动需要 4 天时间。
对于每个活动，列出它的前驱，并计算最早开始时间、最晚开始时间和时差，然后确定出关键路径。
—— 《软件工程 第 4 版》中的原题

写文缘由

网上的文章大都是对于 “点” 求最早开始时间和最晚开始时间。在我看来，是不准确的。

对于边的解法，有的写得又太复杂，还是自己写吧。顺便写个程序自动化一下，舒服~

误区在哪

需要注意的是，图中的点，并不代表活动，并不能说活动 $A$ 用 $3$ 天到达活动 $B$，这是不准确的，图上的点应该理解为 “里程碑”。如果说到达 里程碑 $I$ 的边有两条 $D\to I$ 和 $B\to I$，意思是有两个活动，完成后到达里程碑 $I$，并不能说 $I$ 是个活动，如果这么理解会在计算最晚开始时间时出现错误。

还有一点，时间轴从 $1$ 开始算，即从点 $A$ 出发时，时刻为 $1$。有些解法是从 $0$ 开始算的，本文从 $1$ 开始算。

解法

• 正推求最早开始时间
  • 公式：${\text{ET}}_{B\cdot }=\text{MAX}({\text{ET}}_{AB}+w_{AB})$
  • 已知条件：起点的最早开始时间直接为 1
• 倒推求最晚开始时间
  • 公式：${\text{LT}}_{JK}=\text{MIN}({\text{LT}}_{K\cdot }-w_{JK})$
  • 已知条件：终点的最晚开始时间 ${\text{LT}}_{L\cdot }={\text{ET}}_{L\cdot }$ （因为终点一定在关键路径上，关键路径上的点最早开始时间等于最晚开始时间）

解题示例

解：

先求最早开始时间 (Earliest Time Start)：

• $A$ 是起点，所有由 $A$ 出发的边的最早开始时间都为 $1$。即 ${\text{ET}}_{AB}={\text{ET}}_{AE}={\text{ET}}_{AC}={\text{ET}}_{A\cdot }=1$
• 来算 $B$ 的最早开始时间，${\text{ET}}_{BD}={\text{ET}}_{BI}={\text{ET}}_{B\cdot }=\text{MAX}({\text{ET}}_{AB}+w_{AB})=4$。因为只有 $A$ 才能到达 $B$，所以 MAX 内只有一个值。
• 来算 $E$ 的最早开始时间，${\text{ET}}_{EG}=\text{MAX}({\text{ET}}_{AE}+w_{AE})=5$。因为只有 $A$ 才能到达 $E$，所以 MAX 内只有一个值。
• 来算 $C$ 的最早开始时间，${\text{ET}}_{CF}=\text{MAX}({\text{ET}}_{AC}+w_{AC})=6$。因为只有 $A$ 才能到达 $C$，所以 MAX 内只有一个值。
• 接下来 $D、G、F$ 同理，省去废话，结果是：${\text{ET}}_{DI}=\text{MAX}({\text{ET}}_{BD}+w_{BD})=9$ 、 ${\text{ET}}_{GJ}={\text{ET}}_{GH}={\text{ET}}_{G\cdot }=\text{MAX}({\text{ET}}_{EG}+w_{EG})=8$、${\text{ET}}_{FH}=\text{MAX}({\text{ET}}_{CF}+w_{CF})=9$
• 看一下 $I$，入度为 $2$，${\text{ET}}_{IJ}=\text{MAX}({\text{ET}}_{DI}+w_{DI},{\text{ET}}_{BI}+w_{BI})=\text{MAX}(11,10)=11$，下面的同理
• ${\text{ET}}_{HK}=\text{MAX}({\text{ET}}_{GH}+w_{GH},{\text{ET}}_{FH}+w_{FH})=\text{MAX}(11,10)=11$
• ${\text{ET}}_{JL}={\text{ET}}_{JK}=\text{MAX}({\text{ET}}_{IJ}+w_{IJ},{\text{ET}}_{GJ}+w_{GJ})=\text{MAX}(13,10)=13$
• ${\text{ET}}_{KL}=\text{MAX}({\text{ET}}_{JK}+w_{JK},{\text{ET}}_{HK}+w_{HK})=\text{MAX}(15,15)=15$
• ${\text{ET}}_{L\cdot }=\text{MAX}({\text{ET}}_{JL}+w_{JL},{\text{ET}}_{KL}+w_{KL})=\text{MAX}(21,18)=21$

自此，最早开始时间全部算完。

再求最晚开始时间 (Latest Time Start)：

• 从终点倒着推，${\text{LT}}_{JL}=\text{MIN}({\text{LT}}_{L\cdot }-w_{JL})=13$，${\text{LT}}_{KL}=\text{MIN}({\text{LT}}_{L\cdot }-w_{KL})=18$
• ${\text{LT}}_{JK}=\text{MIN}({\text{LT}}_{KL}-w_{JK})=16$
• ${\text{LT}}_{IJ}=\text{MIN}({\text{LT}}_{JL}-w_{IJ},{\text{LT}}_{JK}-w_{IJ})=11$
• ${\text{LT}}_{GJ}=\text{MIN}({\text{LT}}_{JL}-w_{GJ},{\text{LT}}_{JK}-w_{GJ})=11$
• ${\text{LT}}_{HK}=\text{MIN}({\text{LT}}_{KL}-w_{HK})=14$
• ${\text{LT}}_{DI}=\text{MIN}({\text{LT}}_{IJ}-w_{DI})=9$
• ${\text{LT}}_{BI}=\text{MIN}({\text{LT}}_{IJ}-w_{BI})=5$
• ${\text{LT}}_{GH}=\text{MIN}({\text{LT}}_{HK}-w_{GH})=11$
• ${\text{LT}}_{BD}=\text{MIN}({\text{LT}}_{DI}-w_{BD})=4$
• ${\text{LT}}_{EG}=\text{MIN}({\text{LT}}_{GJ}-w_{GH},{\text{LT}}_{GH}-w_{EG})=8$
• ${\text{LT}}_{FH}=\text{MIN}({\text{LT}}_{HK}-w_{FH})=13$
• ${\text{LT}}_{CF}=\text{MIN}({\text{LT}}_{FH}-w_{CF})=10$
• ${\text{LT}}_{AB}=\text{MIN}({\text{LT}}_{BD}-w_{AB},{\text{LT}}_{BI}-w_{AB})=1$
• ${\text{LT}}_{AE}=\text{MIN}({\text{LT}}_{EG}-w_{AE})=4$
• ${\text{LT}}_{AC}=\text{MIN}({\text{LT}}_{CF}-w_{AC})=5$

（上述过程，看似繁琐，但是考试计算时，在图中对应的边上边写边算，还是挺快的）

根据上述数据，列表如下（其中冗余时间等于最早最晚两者的差）：

活动	前驱	最早开始时间	最晚开始时间	时差（冗余时间）
AB		1	1	0
BD	AB	4	4	0
BI	AB	4	5	1
DI	AB,BD	9	9	0
IJ	AB,BD,DI,BI	11	11	0
AE		1	4	3
EG	AE	5	8	3
GJ	AE,EG	8	11	3
JL	AB,BD,BI,DI,IJ,AE,EG,GJ	13	13	0
AC		1	5	4
CF	AC	6	10	4
FH	AC,CF	9	13	4
GH	AE,EG	8	11	3
HK	AE,EG,GH,AC,CF,FH	11	14	3
JK	AB,BD,BI,DI,IJ,AE,EG,GJ	13	16	3
KL	AB,BD,BI,DI,IJ,AE,EG,GJ,JK,GH,AC,CF,FH,HK	15	18	3

由上述表格可知，$AB、BD、DI、IJ、JL$ 活动的时差为 $0$，即为关键节点，因此关键路径为 $A\to B\to D\to I\to J\to L=20$。

程序实现

诶，写个程序验证一下手算的正确与否吧。

#include 
using namespace std;
#define rep(i,s,t) for(int i=s;i<=t;i++)
const int maxn = 105;
const int INF = 0x3f3f3f3f;

int n, m, S, T;

struct Edge {
     
    int u, v, w, ET, LT;
    Edge(int _u,int _v,int _w,int _ET,int _LT):u(_u),v(_v),w(_w),ET(_ET),LT(_LT){
     }
};
vector<Edge*> G[maxn], GT[maxn], Edges; // 正图和反图

int calcET(Edge *e)
{
     
	if (e->u == S)
        return e->ET = 1;

    for(Edge *ee : GT[e->u])
        e->ET = max(e->ET, (ee->ET==-1?calcET(ee):ee->ET) + ee->w);

	return e->ET;
}

int calcLT(Edge *e)
{
     
	if (e->u == T)
        return e->LT = e->ET;

    for(Edge *ee : G[e->v])
        e->LT = min(e->LT, (ee->LT==INF?calcLT(ee):ee->LT) - e->w);

    return e->LT;
}

bool vis[maxn];
vector<int> path;
void dfs(int u)
{
     
    if (u == T)
    {
     
        path.push_back(u);
        for(int i=0;i<path.size();i++)
            printf(i!=path.size()-1?"%c->":"%c\n", path[i]+'A'-1);
        path.pop_back();
        return;
    }
    vis[u] = true;
    for (Edge *e : G[u])
        if(!vis[e->v] && e->ET==e->LT)
        {
     
            path.push_back(u);
            dfs(e->v);
            path.pop_back();
        }
    vis[u] = false;
    return;
}

char s[5];
int main()
{
     
    freopen("out.txt", "w", stdout);
    scanf("%d%d",&n,&m);
    rep(i,1,m)
    {
     
        int u, v, w;
        scanf("%s", s); u = s[0]-'A'+1;
        scanf("%s", s); v = s[0]-'A'+1;
        scanf("%d", &w);
        Edge* e = new Edge(u, v, w, -1, INF);
        G[u].push_back(e);
        GT[v].push_back(e);
        Edges.push_back(e);
    }
    // 默认 1 是起点, n 是终点，起点入度为 0，终点出度为 0，数据合法。不是的话得改造程序求个拓扑之类的。
	S = 1;
	T = n;
	// 算 ET
	G[T].push_back(new Edge(T, -1, 0, -1, INF));
	calcET(G[T].back());
	// 算 LT
	calcLT(new Edge(-1, S, 0, -1, INF));
	// 输出表
    for(Edge *e : Edges)
        printf("%c%c\t%d\t%d\t%d\n", e->u+'A'-1, e->v+'A'-1, e->ET, e->LT, e->LT-e->ET);
    printf("%c.\t%d\t%d\t%d\n", G[T].back()->u+'A'-1, G[T].back()->ET, G[T].back()->LT, G[T].back()->LT-G[T].back()->ET);
    // 求关键路径
    dfs(S);
	return 0;
}
/*
12 16
A B 3
A E 4
A C 5
B D 5
B I 6
E G 3
C F 3
D I 2
I J 2
G J 2
G H 3
F H 1
J L 8
J K 2
H K 4
K L 3


12 15
A B 2
B C 3
B F 4
B D 2
C E 5
D G 3
E H 2
E F 3
F I 5
G I 6
I J 2
I K 4
J L 1
K L 2
H L 3


12 17
A B 5
A E 3
A C 4
B D 6
B I 4
E G 4
C F 3
D I 3
I J 3
G I 2
G J 7
F G 6
F H 3
J L 9
H J 3
H K 6
K L 2

12 17
A B 5
A E 3
A C 4
B D 6
B I 4
E G 4
C F 3
D I 5
I J 4
G I 2
G J 7
F G 6
F H 3
J L 9
H J 3
H K 6
K L 2

12 17
A B 6
A E 10
A C 4
B D 6
B I 4
E G 4
C F 3
D I 5
F G 6
G I 2
G J 7
I J 4
F H 3
J L 9
H J 3
H K 6
K L 2

*/

尾巴

好的，感谢你看到这里，对文章有错误的地方欢迎指出，谢谢。
如果觉得本文写得不错，不妨点赞、评论、收藏、分享，你的三连是对我最大的支持！

我的 Github：zhangt2333’s Github
我的 CSDN：zhangt2333’s CSDN
我的 博客园：zhangt2333’s cnblog
我的 小书房：https://zhangt.top/

本文作者：zhangt2333
版权声明：本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议 。转载请注明出处！